计算两个n次多项式相乘的最直接方法所需的时间为Θ(n2)\Theta(n^2)Θ(n2),在本文中,我们将讨论快速傅里叶变换(FFT),使得多项式相乘的时间复杂度降为Θ(nlgn)\Theta(n\text{lg}n)Θ(nlgn)。
一、多项式的表示
系数表示和点值表示
对于一个次数界为n的多项式A(x)=∑j=0n−1ajxjA(x)=\sum_{j=0}^{n-1}a_{j}x^jA(x)=∑j=0n−1ajxj而言,其系数表示是一个由系数组成的向量a=(a0,a1,...,an−1)a=(a_{0},a_{1},... ,a_{n-1})a=(a0,a1,...,an−1)。而A(x)A(x)A(x)的点值表示就是一个由n个点组成的集合{(x0,y0),(x1,y1),...(xn−1,yn−1)}\{(x_{0},y_{0}),(x_{1},y_{1}),...(x_{n-1},y_{n-1})\}{(x0,y0),(x1,y1),...(xn−1,yn−1)},使得对k=0,1,...,n−1k=0,1,...,n-1k=0,1,...,n−1,所有xkx_{k}xk各不相同。
对于一个用系数表示的多项式来说,只要选取n个不同的点x0,x1,...,xn−1x_{0},x_{1},...,x_{n-1}x0,x1,...,xn−1,然后在Θ(n2)\Theta(n^2)Θ(n2)的时间内分别计算出各点对应A(x)A(x)A(x)的值,就可以根据这些值解出多项式的系数,这一过程(从一个多项式的点值确定表达式的系数)称为插值。值得注意的是,如果我们可以巧妙地选取nnn个点,那么计算nnn个点对应值的过程所需时间可以降为Θ(nlgn)\Theta(n\lg n)Θ(nlgn)。下面定理说明,当多项式的次数界等于已知的点值对的数目,插值才是正确的。
(插值多项式的唯一性) 对于任意n个点值对组成的集合{(x0,y0),(x1,y1),...(xn−1,yn−1)}\{(x_{0},y_{0}),(x_{1},y_{1}),...(x_{n-1},y_{n-1})\}{(x0,y0),(x1,y1),...(xn−1,yn−1)},其中所有的xkx_{k}xk互不相同,那么存在唯一的一个次数界为n的多项式A(x)A(x)A(x),满足yk=A(xk)y_{k}=A(x_{k})yk=A(xk),k=0,1,…,n-1。
证明 \quad设A(x)A(x)A(x)的系数向量为(a0,a1,...,an−1)(a_{0},a_{1},... ,a_{n-1})(a0,a1,...,an−1),将方程组(1)化为矩阵形式(2):
{A(x0)=a0+a1x0+...+an−1x0=y0A(x1)=a0+a1x1+...+an−1x1=y1⋯A(xn−1)=a0+a1xn−1+...+an−1xn−1=yn−1
\begin{equation}
\begin{cases}
A(x_{0})=a_{0} + a_{1}x_{0}+...+a_{n-1}x_{0}=y_{0}& \\
A(x_{1})=a_{0} + a_{1}x_{1}+...+a_{n-1}x_{1}=y_{1}& \\
\cdots \\
A(x_{n-1})=a_{0} + a_{1}x_{n-1}+...+a_{n-1}x_{n-1}=y_{n-1}& \\
\end{cases}
\end{equation}
⎩⎨⎧A(x0)=a0+a1x0+...+an−1x0=y0A(x1)=a0+a1x1+...+an−1x1=y1⋯A(xn−1)=a0+a1xn−1+...+an−1xn−1=yn−1
[1x0x02⋯x0n−11x1x12⋯x1n−1⋯1xn−1xn−12⋯xn−1n−1][a0a1⋯an−1]=[y0y1⋯yn−1] \begin{equation} \left[ \begin{array}{ccc} 1 & x_{0} & x_{0}^2 & \cdots &x_{0}^{n-1} \\ 1 & x_{1} & x_{1}^2 & \cdots &x_{1}^{n-1} \\ \cdots \\ 1 & x_{n-1} & x_{n-1}^2 & \cdots &x_{n-1}^{n-1} \end{array} \right] \left[ \begin{array}{c} a_{0} \\ a_{1} \\ \cdots \\ a_{n-1} \end{array} \right]= \left[ \begin{array}{c} y_{0} \\ y_{1} \\ \cdots \\ y_{n-1} \end{array} \right] \end{equation} 11⋯1x0x1xn−1x02x12xn−12⋯⋯⋯x0n−1x1n−1xn−1n−1a0a1⋯an−1=y0y1⋯yn−1
左边的矩阵记为V(x0,x1,...,xn−1)V(x_{0},x_{1},...,x_{n-1})V(x0,x1,...,xn−1),根据范德蒙德矩阵的性质,矩阵VVV行列式的值∣V∣=∏0≤j<k≤n−1(xk−xj)≠0|V|=\prod \limits_{0\leq j <k\leq n-1}(x_{k}-x_{j})\neq 0∣V∣=0≤j<k≤n−1∏(xk−xj)=0,因此,VVV是可逆的,故存在唯一的系数矩阵a=V−1ya=V^{-1}ya=V−1y。
对于多项式乘法,点值表达是方便的,设C(x)=A(x)B(x)C(x)=A(x)B(x)C(x)=A(x)B(x),则对于任意点xkx_{k}xk,C(xk)=A(xk)B(xk)C(x_{k})=A(x_{k})B(x_{k})C(xk)=A(xk)B(xk),每次操作的时间为Θ(1)\Theta(1)Θ(1)。由于degree(CCC)=degree(AAA)+degree(BBB),当A和B的次数界都为n时,C的次数界为2n,因此需要对A和B的点值表达式进行扩展,使每个多项式都含2n个点值对。给定A的扩展点值表达{(x0,y0),(x1,y1),...(xn−1,yn−1)}\{(x_{0},y_{0}),(x_{1},y_{1}),...(x_{n-1},y_{n-1})\}{(x0,y0),(x1,y1),...(xn−1,yn−1)}和B的扩展点值表达{(x0,y0′),(x1,y1′),...(xn−1,yn−1′)}\{(x_{0},y_{0}'),(x_{1},y_{1}'),...(x_{n-1},y_{n-1}')\}{(x0,y0′),(x1,y1′),...(xn−1,yn−1′)},则C的点值表达为{(x0,y0y0′),(x1,y1y1′),...(xn−1,yn−1yn−1′)}\{(x_{0},y_{0}y_{0}'),(x_{1},y_{1}y_{1}'),...(x_{n-1},y_{n-1}y_{n-1}')\}{(x0,y0y0′),(x1,y1y1′),...(xn−1,yn−1yn−1′)}。给定两个点值扩展形式的输入多项式,得到其相乘结果的点值形式所需时间为Θ(n)\Theta(n)Θ(n)。
系数形式表示多项式的快速乘法
我们需要利用基于点值形式表达的多项式线性时间乘法算法,来加速基于系数形式表达的多项式乘法运算。关键在于快速将一个多项式从系数形式转换为点值形式(求值)以及从点值形式转换为系数形式(插值)。
通过巧妙地选择求值点,我们可以把两种表示方法之间的转换所需的时间复杂度变为Θ(nlgn)\Theta(nlgn)Θ(nlgn),在第二节中选择单位复数根作为求值点,对系数向量做离散傅里叶变换(DFT),得到对应的点值表达,同样我们可以通过对这些点值执行逆DFT变换,获得其相应的系数向量,这样就实现了插值运算。
如下图所示,两个次数界为n的多项式的乘积是一个次数界为2n的多项式,因此,在输入多项式A和B进行求值前,先把这两个多项式在最高次系数前添加n个0,使其次数界增大为2n。
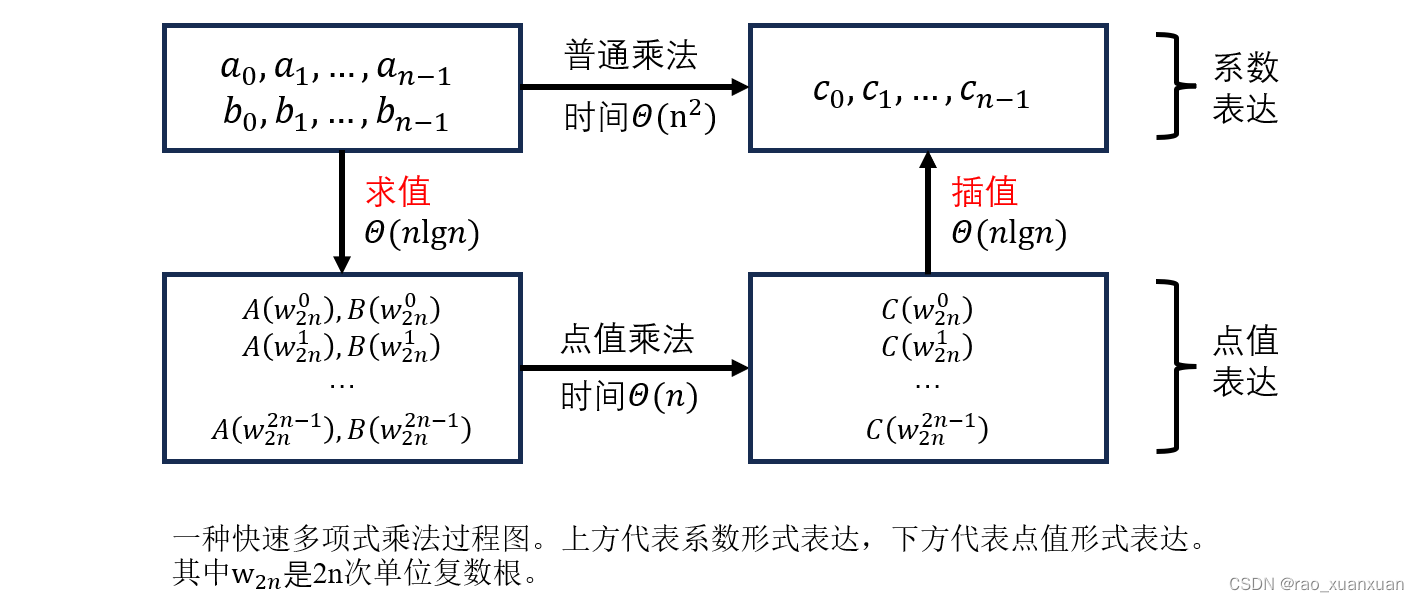
给定FFT,我们就有下面时间复杂度为Θ(nlgn)\Theta(n\lg n)Θ(nlgn)的算法,把两个次数界为n的多项式A(x)A(x)A(x)和B(x)B(x)B(x)进行乘法运算,其中输入和输出均以系数表达,假设n是2的幂(实际可以通过向高阶系数补0的方式来满足这个要求):
- 加倍次数界:通过加入n个系数为0的高阶系数,把多项式A(x)A(x)A(x)和B(x)B(x)B(x)变为次数界为2n的多项式,并构造其系数表达。
- 求值:通过应用2n阶的FFT计算出A(x)A(x)A(x)和B(x)B(x)B(x)的长度为2n的点值表达,这些点值表达包含了两个多项式在2n次单位根处的取值。
- 逐点相乘:把A(x)A(x)A(x)的值和B(x)B(x)B(x)的值逐点相乘,可以计算多项式C(x)=A(x)B(x)C(x)=A(x)B(x)C(x)=A(x)B(x)的点值表达,这个点值表达包含了C(x)C(x)C(x)在每个2n次单位根处的取值。
- 插值:通过对2n个点值对应用FFT,计算其逆DFT,就可以构造出多项式C(x)C(x)C(x)的系数表达。
其中,执行第一步和第三步的时间为Θ(n)\Theta(n)Θ(n),执行第二步和第四步的时间为Θ(nlgn)\Theta(n\lg n)Θ(nlgn)。
二、DFT与FFT
单位复数根
n次单位复数根是满足wn=1w^n=1wn=1的复数www。n次单位复数根恰好有n个:对于k=0,1,⋯ ,n−1k=0,1,\cdots,n-1k=0,1,⋯,n−1,这些根是e2πik/ne^{2\pi ik/n}e2πik/n。这里我们通过欧拉定理用指数形式表示复数:eiu=cos(u)+isin(u)e^{iu}=\cos(u)+i\sin (u)eiu=cos(u)+isin(u),下图说明nnn个单位复数根均匀地分布在以复平面的原点为圆心的单位圆周上,wn=e2πi/nw_{n}=e^{2\pi i/n}wn=e2πi/n称为主nnn次单位根,其他所有n次单位复数根都是wnw_{n}wn的幂次。
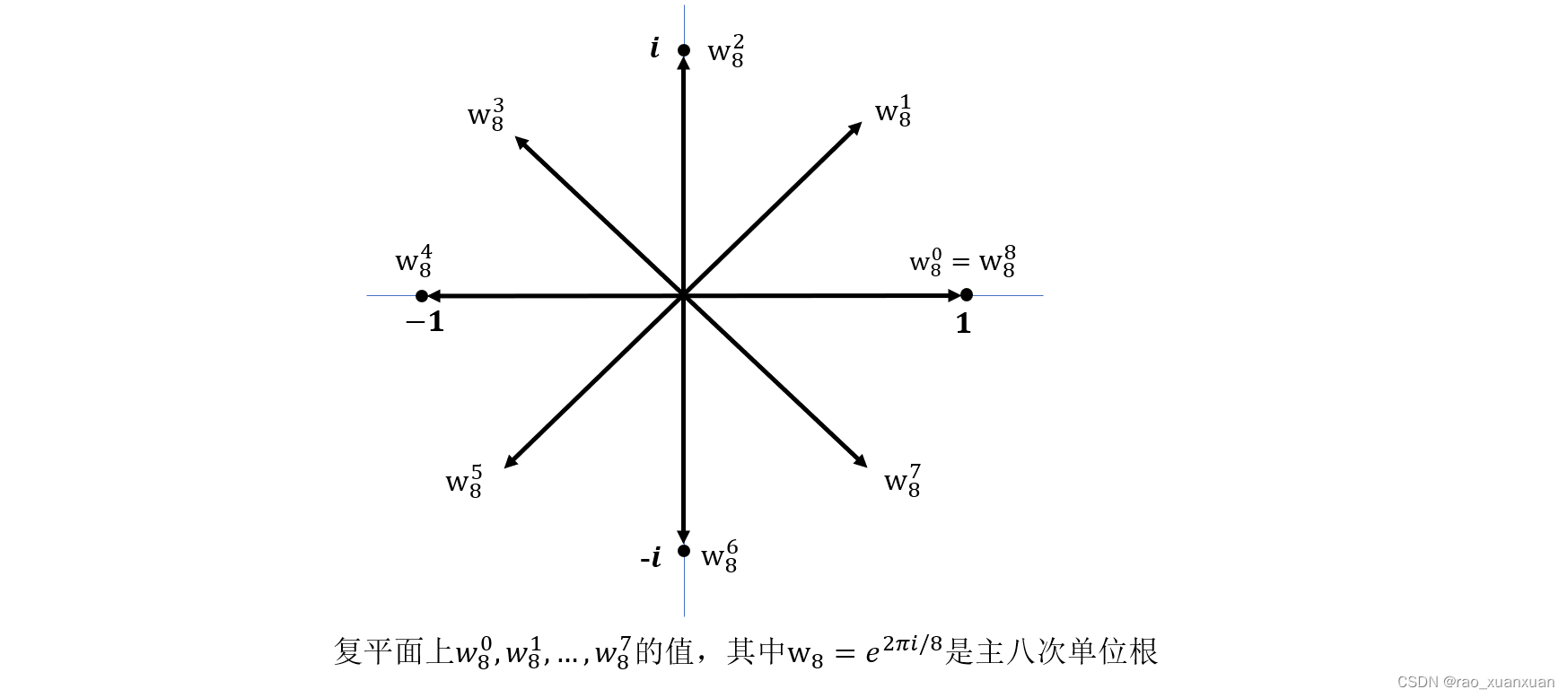
n个n次单位复数根wn0,wn1,⋯ ,wnn−1w_{n}^0,w_{n}^1,\cdots,w_{n}^{n-1}wn0,wn1,⋯,wnn−1在乘法意义下形成一个群,该群与加法群(整数模n)具有同样的结构,即wnn=wn0w_{n}^n=w_{n}^0wnn=wn0意味着wnjwnk=wn(j+k)%nw_{n}^jw_{n}^k=w_{n}^{(j+k)\%n}wnjwnk=wn(j+k)%n。对于n次单位复数根有以下性质:
(消去引理) 1. 对于任何整数n≥0,k≥0n\geq0,k\geq0n≥0,k≥0以及d>0d>0d>0,有wdndk=wnkw_{dn}^{dk}=w_{n}^kwdndk=wnk。
(折半引理) 2. 如果n>0n>0n>0为偶数,那么n个n次单位复数根的平方的集合就是n/2n/2n/2个n/2n/2n/2次单位复数根的集合。
(求和引理) 3. 对任意整数n≥1n\geq 1n≥1和不能被nnn整除的非负整数kkk,有∑j=0n−1(wnk)j=0\sum_{j=0}^{n-1}(w_{n}^k)^j=0j=0∑n−1(wnk)j=0
DFT
我们希望计算次数界为n的多项式A(x)=∑j=0n−1ajxjA(x)=\sum_{j=0}^{n-1}a_{j}x^jA(x)=∑j=0n−1ajxj在nnn个单位复数根wn0,wn1,⋯ ,wnn−1w_{n}^0,w_{n}^1,\cdots,w_{n}^{n-1}wn0,wn1,⋯,wnn−1处的值。假设AAA以系数形式给出:a=(a0,a1,⋯ ,an−1)a=(a_{0},a_{1},\cdots,a_{n-1})a=(a0,a1,⋯,an−1),接下来对k=0,1,⋯ ,n−1k=0,1,\cdots,n-1k=0,1,⋯,n−1,定义结果yky_{k}yk:yk=A(wnk)=∑j=0n−1ajwnkj\begin{equation} y_{k}=A(w_{n}^k)=\sum_{j=0}^{n-1}a_{j}w_{n}^{kj} \end{equation} yk=A(wnk)=j=0∑n−1ajwnkj向量y=(y0,y1,⋯ ,yn−1)y=(y_{0},y_{1},\cdots,y_{n-1})y=(y0,y1,⋯,yn−1)就是系数向量a=(a0,a1,⋯ ,an−1)a=(a_{0},a_{1},\cdots,a_{n-1})a=(a0,a1,⋯,an−1)的离散傅里叶变换(DFT),记为y=DFTn(a)y=DFT_{n}(a)y=DFTn(a)。
FFT
通过使用一种称为快速傅里叶变换(FFT)的方法,利用单位复数根的性质,我们就可以在Θ(nlgn)\Theta(nlgn)Θ(nlgn)的时间内计算出DFTn(a)DFT_{n}(a)DFTn(a),这里假设nnn恰好是2的整数幂。
FFT采用了分治策略,采用A(x)A(x)A(x)中偶数下标的系数和奇数下标的系数,分别定义两个新的次数界为n/2n/2n/2的多项式A[0](x)A^{[0]}(x)A[0](x)和A[1](x)A^{[1]}(x)A[1](x):
A[0](x)=a0+a2x+a4x2+⋯+an−2xn/2−1A[1](x)=a1+a3x+a5x2+⋯+an−1xn/2−1
A^{[0]}(x)=a_{0}+a_{2}x+a_{4}x^2+\cdots+a_{n-2}x^{n/2-1} \\
A^{[1]}(x)=a_{1}+a_{3}x+a_{5}x^2+\cdots+a_{n-1}x^{n/2-1}
A[0](x)=a0+a2x+a4x2+⋯+an−2xn/2−1A[1](x)=a1+a3x+a5x2+⋯+an−1xn/2−1
注意到,A[0](x)A^{[0]}(x)A[0](x)包含AAA中所有偶数下标的系数,A[1](x)A^{[1]}(x)A[1](x)包含AAA中所有奇数下标的系数,于是有
A(x)=A[0](x2)+xA[1](x2)
\begin{equation}
A(x)=A^{[0]}(x^2)+xA^{[1]}(x^2)
\end{equation}
A(x)=A[0](x2)+xA[1](x2)
于是原问题转化为:
- 求次数界为n/2n/2n/2的多项式A[0](x)A^{[0]}(x)A[0](x)和A[1](x)A^{[1]}(x)A[1](x)在点(wn0)2,(wn1)2,⋯ ,(wnn−1)2(w_{n}^0)^2,(w_{n}^1)^2,\cdots,(w_{n}^{n-1})^2(wn0)2,(wn1)2,⋯,(wnn−1)2处的取值
- 根据式(4)综合上述结果得到A(x)A(x)A(x)的值,即DFTnDFT_{n}DFTn
根据折半引理,(wn0)2,(wn1)2,⋯ ,(wnn−1)2(w_{n}^0)^2,(w_{n}^1)^2,\cdots,(w_{n}^{n-1})^2(wn0)2,(wn1)2,⋯,(wnn−1)2可以看作仅由n/2个n/2次单位复数根所组成,每个根正好出现两次,因此,可以递归地对次数界为n/2的多项式A[0](x)A^{[0]}(x)A[0](x)和A[1](x)A^{[1]}(x)A[1](x)在n/2n/2n/2个n/2n/2n/2次单位复数根处进行求值。这些子问题与原问题形式相同,但规模减小为原问题的一半,即将一个n个元素的DFTnDFT_{n}DFTn划分为两个规模为n/2n/2n/2个元素的DFTn/2DFT_{n/2}DFTn/2。这一分解是下面递归FFT算法的基础,此算法计算出一个由nnn个元素组成的向量a=(a0,a1,⋯ ,an−1)a=(a_{0},a_{1},\cdots,a_{n-1})a=(a0,a1,⋯,an−1)的DFTnDFT_{n}DFTn,其中nnn是2的幂。

RECURSIVE-FFT的执行过程如下:
第2-3行是递归的基础,一个元素的DFT就是它本身,因为在这种情形下,y0=a0w10=a0y_{0}=a_{0}w_{1}^0=a_{0}y0=a0w10=a0。
第6-7行定义多项式A[0](x)A^{[0]}(x)A[0](x)和A[1](x)A^{[1]}(x)A[1](x)的系数向量,第4、5、13行保证www可以正确更新,在执行第11-12行时,始终有w=wnkw=w_{n}^kw=wnk。第8-9行递归执行DFTn/2DFT_{n/2}DFTn/2,对于k=0,1,⋯ ,n−1k=0,1,\cdots,n-1k=0,1,⋯,n−1,
yk[0]=A[0](wn/2k)=A[0](wn2k)yk[1]=A[1](wn/2k)=A[1](wn2k)
y_{k}^{[0]} = A^{[0]}(w_{n/2}^k) = A^{[0]}(w_{n}^{2k})\\
y_{k}^{[1]} = A^{[1]}(w_{n/2}^k) = A^{[1]}(w_{n}^{2k})
yk[0]=A[0](wn/2k)=A[0](wn2k)yk[1]=A[1](wn/2k)=A[1](wn2k)
第11-12行综合了递归DFTn/2DFT_{n/2}DFTn/2的结果,对y0,y1,⋯ ,yn/2−1y_{0},y_{1},\cdots,y_{n/2-1}y0,y1,⋯,yn/2−1,第11行推出:
yk=yk[0]+wnkyk[1]=A[0](wn2k)+wnkA[1](wn2k)=A(wnk)式(4)
\begin{align*}
y_{k} &= y_{k}^{[0]}+w_{n}^k y_{k}^{[1]}\\
&=A^{[0]}(w_{n}^{2k})+w_{n}^kA^{[1]}(w_{n}^{2k})\\
&=A(w_{n}^k) \qquad \qquad \qquad \qquad \qquad \qquad \quad 式(4)
\end{align*}
yk=yk[0]+wnkyk[1]=A[0](wn2k)+wnkA[1](wn2k)=A(wnk)式(4)
对yn/2,yn/2+1,⋯ ,yn−1y_{n/2},y_{n/2+1},\cdots,y_{n-1}yn/2,yn/2+1,⋯,yn−1,设k=0,1,⋯ ,n/2−1k=0,1,\cdots,n/2-1k=0,1,⋯,n/2−1,第12行推出:
yk+n/2=yk[0]−wnkyk[1]=A[0](wn2k)+wnk+n/2A[1](wn2k)折半引理=A[0](wn2k+n)+wnk+n/2A[1](wn2k+n)=A(wnk+n/2)式(4)
\begin{align*}
y_{k+n/2}&=y_{k}^{[0]}-w_{n}^ky_{k}^{[1]}\\
&=A^{[0]}(w_{n}^{2k})+w_{n}^{k+n/2} A^{[1]}(w_{n}^{2k})\qquad \qquad \enspace折半引理\\
&=A^{[0]}(w_{n}^{2k+n})+w_{n}^{k+n/2}A^{[1]}(w_{n}^{2k+n})\\
&=A(w_{n}^{k+n/2})\qquad \qquad \qquad \qquad \qquad \qquad 式(4)
\end{align*}
yk+n/2=yk[0]−wnkyk[1]=A[0](wn2k)+wnk+n/2A[1](wn2k)折半引理=A[0](wn2k+n)+wnk+n/2A[1](wn2k+n)=A(wnk+n/2)式(4)
至此,RECURSIVE-FFT的正确性得以证明,它可以返回输入向量aaa的DFT。
关于RECURISVE-FFT的执行时间,我们可以通过该递归式得到:T(n)=2T(n/2)+Θ(n)=Θ(nlgn)T(n)=2T(n/2)+\Theta(n)=\Theta(nlgn)T(n)=2T(n/2)+Θ(n)=Θ(nlgn)。这里的nnn是输入向量aaa的长度,每次除递归调用外,所需时间为算法第10-13行的for循环所消耗Θ(n)\Theta(n)Θ(n),因此上述递归式成立。
在单位复数根处插值
接下来我们需要在单位复数根处插值将多项式由点值表达转化为系数表达,首先将DFT写成矩阵方程,然后观察它逆矩阵的形式。
根据式(2),我们可以把DFT写成矩阵乘积y=Vnay=V_{n}ay=Vna,其中VnV_{n}Vn是一个由wnw_{n}wn适当幂次填充成的范德蒙德矩阵:
[y0y1y2⋯yn−1]=[111⋯11wn1wn2⋯wnn−11wn2wn4⋯wn2(n−1)⋯1wnn−1wn2(n−1)⋯wn(n−1)(n−1)][a0a1a2⋯an−1]
\begin{equation}
\left[
\begin{array}{c}
y_{0} \\
y_{1} \\
y_{2} \\
\cdots \\
y_{n-1}
\end{array}
\right]=
\left[
\begin{array}{ccc}
1 & 1 & 1 & \cdots &1 \\
1 & w_{n}^1 & w_{n}^2 & \cdots &w_{n}^{n-1} \\
1 & w_{n}^2 & w_{n}^4 & \cdots &w_{n}^{2(n-1)} \\
\cdots \\
1 & w_{n}^{n-1} & w_{n}^{2(n-1)} & \cdots &w_{n}^{(n-1)(n-1)}
\end{array}
\right]
\left[
\begin{array}{c}
a_{0} \\
a_{1} \\
a_{2} \\
\cdots \\
a_{n-1}
\end{array}
\right]
\end{equation}
y0y1y2⋯yn−1=111⋯11wn1wn2wnn−11wn2wn4wn2(n−1)⋯⋯⋯⋯1wnn−1wn2(n−1)wn(n−1)(n−1)a0a1a2⋯an−1
对j,k=0,1,⋯ ,n−1j,k=0,1,\cdots,n-1j,k=0,1,⋯,n−1,VnV_{n}Vn的(k,j)(k,j)(k,j)处元素为wnkjw_{n}^{kj}wnkj。对于逆运算DFT−1DFT^{-1}DFT−1,我们把yyy乘以VnV_{n}Vn的逆矩阵Vn−1V_{n}^{-1}Vn−1来处理得到系数向量aaa。
对j,k=0,1,⋯ ,n−1j,k=0,1,\cdots,n-1j,k=0,1,⋯,n−1,Vn−1V_{n}^{-1}Vn−1的(j,k)(j,k)(j,k)处元素为wn−kj/nw_{n}^{-kj}/nwn−kj/n。
证明 \quad 已知Vn−1Vn=InV_{n}^{-1}V_{n}=I_{n}Vn−1Vn=In。考虑矩阵乘法结果在(j,j′)(j,j')(j,j′)处的元素:
[Vn−1Vn]jj′=∑k=0n−1(wn−kj/n)(wnkj′)=∑k=0n−1(wnk(j′−j)/n)[V_{n}^{-1}V_{n}]_{jj'}=\sum_{k=0}^{n-1}(w_{n}^{-kj}/n)(w_{n}^{kj'})=\sum_{k=0}^{n-1}(w_{n}^{k(j'-j)}/n)[Vn−1Vn]jj′=k=0∑n−1(wn−kj/n)(wnkj′)=k=0∑n−1(wnk(j′−j)/n)
如果j′=jj'=jj′=j,则结果为∑k=0n−11n=1\sum_{k=0}^{n-1}\frac{1}{n}=1∑k=0n−1n1=1;否则,根据求和引理(j′−jj'-jj′−j不能被nnn整除),结果为0。
因此,给定逆矩阵Vn−1V_{n}^{-1}Vn−1,可以推导出DFTn−1(y)DFT_{n}^{-1}(y)DFTn−1(y):
aj=1n∑k=0n−1ykwn−kj
\begin{equation}
a_{j}=\frac{1}{n}\sum_{k=0}^{n-1}y_{k}w_{n}^{-kj}
\end{equation}
aj=n1k=0∑n−1ykwn−kj
将上式(6)与式(3):yk=A(wnk)=∑j=0n−1ajwnkjy_{k}=A(w_{n}^k)=\sum_{j=0}^{n-1}a_{j}w_{n}^{kj}yk=A(wnk)=∑j=0n−1ajwnkj对比,可以得到只需要对FFT算法做出如下修改就可以在Θ(nlgn)\Theta(nlgn)Θ(nlgn)的时间内计算出DFTn−1DFT_{n}^{-1}DFTn−1:将aaa与yyy互换,用wn−1w_{n}^{-1}wn−1替换wnw_{n}wn,并将结果的每个元素除以nnn。

快速傅里叶变换的代码实现
根据上述分析,求值和插值的过程可以共用一份代码,唯一不同的是wnw_{n}wn和结果向量是否需要除以长度。在求值过程,wn=e2πi/n=cos(2πn)+sin(2πn)iw_{n}=e^{2\pi i/n}=\cos(\frac{2\pi}{n})+\sin(\frac{2\pi}{n})iwn=e2πi/n=cos(n2π)+sin(n2π)i;在求值过程中,wn=e−2πi/n=cos(−2πn)+sin(−2πn)i=cos(2πn)−sin(2πn)iw_{n}=e^{-2\pi i/n}=\cos(-\frac{2\pi}{n})+\sin(-\frac{2\pi}{n})i=\cos(\frac{2\pi}{n})-\sin(\frac{2\pi}{n})iwn=e−2πi/n=cos(−n2π)+sin(−n2π)i=cos(n2π)−sin(n2π)i。可以发现,二者仅在虚部符号相反,因此可以在算法中加入一个参数opopop乘以wnw_{n}wn虚部的值:当op=1op=1op=1,表示进行FFT;当op=−1op=-1op=−1,表示进行IFFT。
下面是快速傅里叶变换算法的代码:
void FFT(plural A[], int n, int op)
{
if (n == 1) return;
plural A1[n] = { 0 };
plural A2[n] = { 0 };
for (int i = 0; i < n / 2; i++) {
A1[i] = A[i * 2];
A2[i] = A[i * 2 + 1];
}
FFT(A1, n / 2, op);
FFT(A2, n / 2, op);
plural w, w_n;
w_n.real = cos(2.0 * Pi / n);
w_n.img = sin(2.0 * Pi / n) * op;
w.real = 1; w.img = 0;
for (int i = 0; i < n / 2; i++)
{
A[i] = add(A1[i], mul(A2[i], w));
A[i + n / 2] = sub(A1[i], mul(A2[i], w));
w = mul(w, w_n);
}
}
调用方式如下:
memset(A, 0, sizeof(A));
memset(B, 0, sizeof(B));
// 输入 A、B的系数向量
input(A, B);
FFT(A, n, 1); // 计算A在单位复数根处的值
FFT(B, n, 1); // 计算B在单位复数根处的值
// 以点值形式表示的多项式相乘,结果存储在A中
for (int i = 0; i < n; i++)
A[i] = mul(A[i], B[i]);
// 插值操作,由点值形式转化为系数形式
FFT(A, n, -1);
for(int i = 0; i < n; i++)
printf("%d ",(int)(A[i].real/n + 0.5));
三、高效FFT的实现
FFT的一种迭代实现
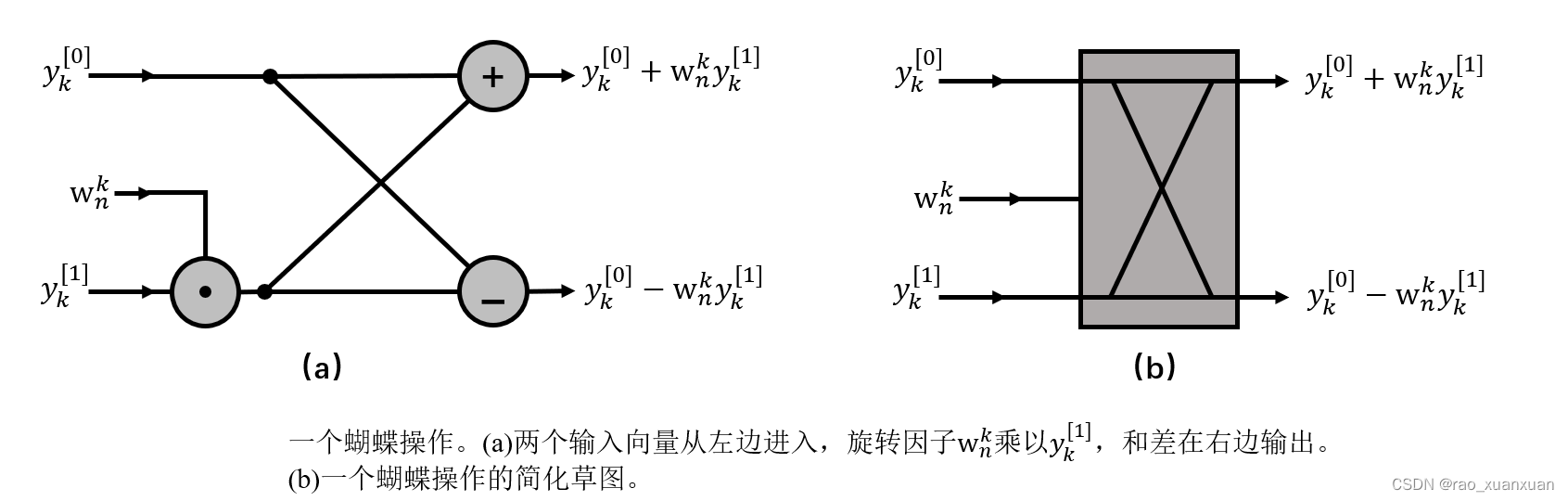
首先我们注意到,在RECURSIVE-FFT中,第10-13行的for循环中包含了wnkyk[1]w_{n}^{k}y_{k}^{[1]}wnkyk[1]的两次计算,我们称该值为公用子表达式,我们可以改变循环,使其仅计算一次,并将其存储到变量中。
for k=0 to n/2−1t=wyk[1]yk=yk[0]+tyk+(n/2)=yk[0]−tw=wwn\qquad\qquad\textbf{for}\space k=0\space \textbf{to} \space n/2-1\\ \qquad\qquad \qquad t = wy_{k}^{[1]} \\ \qquad\qquad \qquad y_{k}=y_{k}^{[0]}+t\\ \qquad\qquad \qquad y_{k+(n/2)}=y_{k}^{[0]}-t \\ \qquad\qquad \qquad w=ww_{n}for k=0 to n/2−1t=wyk[1]yk=yk[0]+tyk+(n/2)=yk[0]−tw=wwn
在这个循环中,我们将循环因子wnw_{n}wn乘以yk[1]y_{k}^{[1]}yk[1],把所得结果存入变量ttt中,然后从yk[0]y_{k}^{[0]}yk[0]增加或减去ttt,这一系列操作被称为一个蝴蝶操作(butterfly operation),下图说明了操作执行步骤:
接下来将算法的递归结构修改为迭代结构。下图是输入一个长度n=8的向量RECURSIVE-FFT执行过程中的递归结构(一棵向量树),树中的每一个节点对应每次过程的递归调用,由相应的输入向量标记。每次RECURSIVE-FFT调用产生两个递归调用,除非该调用已收到了1个元素的向量,第一次调用作为左孩子,第二次调用作为右孩子。

只要把初始向量aaa中的元素按照其在叶中出现次序进行安排,就可以对过程RECURSIVE-FFT的执行进行追踪,不过是自底向上而不是自顶向下。首先,我们成对地提取出元素,利用一次蝴蝶操作计算出每对的DFT,然后对其DFT取代这对元素,这样向量中就包含了n/2n/2n/2个二元素的DFT。下一步,按对取出这n/2n/2n/2个DFT,通过两次DFT蝴蝶操作计算出具有n/4n/4n/4个四元素的DFT,并用一个具有四个元素的DFT取代对应的两个二元素的DFT。继续这样的操作,直到向量包含两个具有n/2n/2n/2个元素的DFT,这时,我们可以综合n/2n/2n/2次蝴蝶操作,合成具有nnn个元素的DFT了。
我们用一个数组A[0 … n-1],初始时该数组包含输入向量aaa中的元素,其顺序为上图递归树中树叶顺序(得到这一序列的过程称为位逆序置换)。因为需要在树的每一层进行组合,于是引入变量sss来计算树的层次,其取值范围为从111到lgn\lg nlgn,因此,该算法有以下结构:
1for s=1 to lgn2for k=0 to n−1 by 2s3combine the two 2s−1-element DFTs in A[k⋯k+2s−1−1] and A[k+2s−1⋯k+2s−1] into one 2s-element DFT in A[k⋯k+2s−1]1\quad \textbf{for} \space s=1\space \textbf{to}\space \lg n\\ 2 \qquad \quad \textbf{for} \space k=0\space \textbf{to}\space n-1\space \textbf{by} \space2^s \\ 3\qquad \qquad \quad \text{combine the two}\space 2^{s-1}\text{-element DFTs in} \space A[k\cdots k+2^{s-1}-1]\space \text{and}\space A[k+2^{s-1}\cdots k+2^{s}-1]\\ \qquad \qquad \space \quad \text{ into one}\space 2^s\text{-element DFT in }A[k\cdots k+2^s-1]1for s=1 to lgn2for k=0 to n−1 by 2s3combine the two 2s−1-element DFTs in A[k⋯k+2s−1−1] and A[k+2s−1⋯k+2s−1] into one 2s-element DFT in A[k⋯k+2s−1]
可以通过如下方式实现上述算法:从子程序RECURSIVE-FFT中复制for循环,让y[0]y^{[0]}y[0]与A[k⋯k+2s−1−1]A[k\cdots k+2^{s-1}-1]A[k⋯k+2s−1−1]一致,让y[1]y^{[1]}y[1]与A[k+2s−1⋯k+2s−1]A[k+2^{s-1}\cdots k+2^{s}-1]A[k+2s−1⋯k+2s−1]一致。在每次蝴蝶操作中,使用的旋转因子依赖于sss的值,它是w2sw_{2^s}w2s的幂,我们引入临时变量uuu使得它能恰当地执行蝴蝶操作(数据不会被覆盖)。用循环主体代替上述算法第三行内容,就可以得到下面的伪代码,代码首先调用辅助过程BIT-REVERSE,把向量aaa按我们所需要的初始顺序复制到数组AAA中。

接下来考虑BIT-REVERSE是如何将输入向量aaa按希望顺序放入数组AAA中。在递归树中,叶出现顺序是一个位逆序置换,也就是说,如果让rev(k)rev(k)rev(k)为kkk的二进制表示各位逆序所形成的lgn\lg nlgn位数,那么我们希望把向量中的元素aka_kak放在数组的A[rev(k)]A[rev(k)]A[rev(k)]位置上。如下表所示,当k=3k=3k=3,rev(k)=110rev(k)=110rev(k)=110,也就是说a3a_3a3出现在A[6]A[6]A[6]处。
| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| aaa | a0a_0a0 | a1a_1a1 | a2a_2a2 | a3a_3a3 | a4a_4a4 | a5a_5a5 | a6a_6a6 | a7a_7a7 |
| 二进制 | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
| AAA | a0a_0a0 | a4a_4a4 | a2a_2a2 | a6a_6a6 | a1a_1a1 | a5a_5a5 | a3a_3a3 | a7a_7a7 |
| 二进制rev(index) | 000 | 100 | 010 | 110 | 001 | 101 | 011 | 111 |
注意到在树的最顶层,最低位为0的下标在左子树中,最低位为1的下标在右子树中。在每一层去掉最低位后,我们沿着树往下继续这一过程,直到在叶子处得到由位逆序置换给出的顺序。于是BIT-REVERSE过程如下:
BIT-REVERSE(a,A)1n=a.length2for k=0 to n−13A[rev(k)]=ak\qquad \text{BIT-REVERSE}(a,A)\\ \qquad1 \qquad n=a.length \\ \qquad2 \qquad \textbf{for}\space k=0 \space \textbf{to} \space n-1\\ \qquad3\qquad \qquad A[rev(k)]=a_kBIT-REVERSE(a,A)1n=a.length2for k=0 to n−13A[rev(k)]=ak
这种迭代方式实现的时间位Θ(nlgn)\Theta(n\lg n)Θ(nlgn),这是由于迭代了nnn次,每次迭代可以在O(lgn)O(\lg n)O(lgn)的时间内把一个介于0和n-1的lgn\lg nlgn位数逆序。
在实际中通常可以通过预处理,在Θ(n)\Theta(n)Θ(n)的时间内完成位逆序置换。在aaa中偶数下标处的位逆序置换结果二进制首位为0,奇数位下标处的位逆序置换结果二进制首位为1;如果按照0-1,2-3的方式分组,每两个相邻的二进制数除首位外其余位都相同,并且除首位外是上一级子问题的解;AAA中前一半(A[0]A[0]A[0]到A[n/2−1]A[n/2-1]A[n/2−1])二进制数除最后一位外是上一级子问题的解。综上,rev[k]rev[k]rev[k]有如下关系:
rev[k]=(rev[k/2]>>1) ∣ ((k&1)×n2)
rev[k]=(rev[k/2]>>1)\space |\space ((k\&1)\times \frac{n}{2})
rev[k]=(rev[k/2]>>1) ∣ ((k&1)×2n)
并行FFT电路
我们可以利用迭代FFT算法的性质来产生一个高效的并行FFT算法。如下图所示,输入长度为n=8n=8n=8的向量aaa,用一个并行FFT电路计算FFT。该电路开始时对输入进行位逆序置换,其后电路分lgn\lg nlgn级,每一级由n/2n/2n/2个并行执行的蝴蝶操作组成。电路的深度定义为任意的输入和任意的输出之间最大的可以达到的计算元素的数目,因此,并行FFT电路的深度为Θ(lgn)\Theta(\lg n)Θ(lgn)。
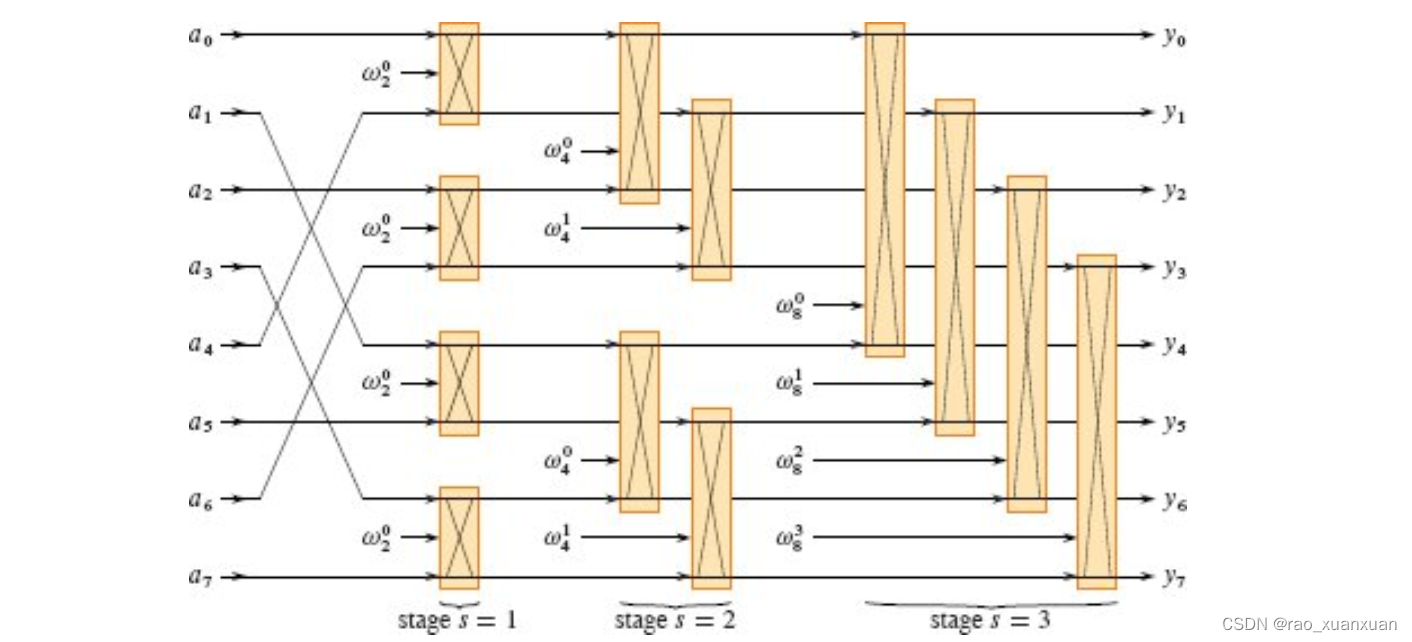
并行FFT电路的最外层执行位逆序操作,其余部分模拟迭代的ITERATIVE-FFT过程。因为最外层for循环的每次迭代执行n/2n/2n/2次独立的蝴蝶操作,于是电路并行地执行它们。在ITERATIVE-FFT内每次迭代的值sss对应于上图中一个阶段的蝴蝶操作,对于s=1,2,⋯ ,lgns=1,2,\cdots,\lg ns=1,2,⋯,lgn,阶段sss有n/2sn/2^sn/2s组蝴蝶操作,每组中有2s−12^{s-1}2s−1个蝴蝶操作。蝴蝶操作用到的旋转因子对应于ITERATIVE-FFT中所用的旋转因子:在阶段sss,我们使用wm0,wm1,⋯ ,wmm/2−1w_{m}^0,w_{m}^1,\cdots, w_{m}^{m/2-1}wm0,wm1,⋯,wmm/2−1,其中m=2sm=2^sm=2s。





 本文详细介绍了快速傅里叶变换(FFT)如何降低多项式乘法的时间复杂度,从传统的平方时间复杂度优化至线性对数时间复杂度。通过点值表示和系数表示的转换,结合单位复数根的性质,阐述了FFT的基本思想和计算过程。此外,还讨论了FFT的递归实现和迭代实现,以及并行FFT电路的设计,展示了FFT在数值计算中的高效性。
本文详细介绍了快速傅里叶变换(FFT)如何降低多项式乘法的时间复杂度,从传统的平方时间复杂度优化至线性对数时间复杂度。通过点值表示和系数表示的转换,结合单位复数根的性质,阐述了FFT的基本思想和计算过程。此外,还讨论了FFT的递归实现和迭代实现,以及并行FFT电路的设计,展示了FFT在数值计算中的高效性。

















 5495
5495

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










