路飞&上楼

众所周知，路飞有一个神奇的能力，就是可以把他的腿无限伸长（因为他吃了橡胶果实

现在他的眼前有n个楼梯，每个楼梯都比上一次高ai​（地面从0开始）如果路飞的腿长比楼梯的高度差小的话，他就跨不过这个楼梯,他想知道，在他的腿的长度为k的时候，他最多能到达的高度为多少？（路飞目前的高度是0）。

输入描述

第一行包含一个整数t(1≤t≤100)——测试用例的数量。
每个测试用例的第一行包含两个整数n,q(1≤n,q≤2⋅105)——分别为楼梯的数量和询问的次数。
每个测试用例的第二行包含n个整数(1≤ai​≤109)—每个楼梯和上一个的高度差。
每个测试用例的第三行包含q个整数(0≤ki​≤109)——每次路飞的腿的长度。
保证n的总和不超过2⋅105,q的总和不超过2⋅105。

输出描述

对于每个测试用例，
一行进行q次回答
输出每次路飞的腿长的对应的能够到达的最高的楼梯的长度。

用例输入 1 

2
4 5
1 2 1 5
1 2 4 9 10
2 2
1 1
0 1

用例输出 1 

1 4 4 9 9 
0 2 

提示

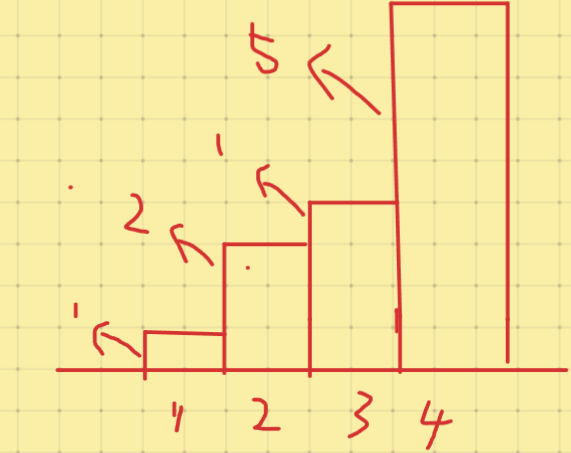
考虑第一个样例，如图所示。
如果路飞的腿长是1，那么他只能爬第1级楼梯，所以他能爬到的高度最高是1米。
如果路飞的腿长度为2或4，那么他只能爬第1、2、3级楼梯，所以他能爬到的高度最高是1+2+1=4米。
如果路飞的腿长是9或10，那么他可以爬上整个楼梯，所以他能爬到的最高的高度是1+2+1+5=9米。

来源

NYOJ

这道题刚开始用暴力做的，超时了，然后想的是动态规划dp re了原因是这个数据范围太大了数组开不了这莫大的空间，最后想到是二分真是万万没想到。

这道题的解题思路：首先将路飞的腿的长从小到大排序，然后依次算出路飞腿长能爬倒最高楼层把他们依次存到数组ans里最后进行二分查找废话不多说直接上代码。

#include<bits/stdc++.h>
using namespace std;
int a[200005],b[200005],k[200005];
long long ans[200005];
int main()
{
    int t;
    cin>>t;
    while(t--)
    { memset(ans,0,sizeof(ans));
int n,q;
    cin>>n>>q;
    for(int i=1;i<=n;i++)
        cin>>a[i];
        for(int i=1;i<=q;i++)
        {
            cin>>k[i];
            b[i]=k[i];
        }
        sort(b+1,b+q+1);
        long long t=1;
        long long sum=0;
        for(int i=1;i<=q;i++)
        {
            for(int j=t;j<=n;j++)
            {
                if(b[i]>=a[j])
                {
                    sum=sum+a[j];
                    if(j==n)//这一步爬到了最高楼层后面爬的最高楼层都一样了
                    {
                        t=n+1;
                    }
                }
                
                else//如果腿没内长就跳出循环保留当前的位置
                {
                    t=j;
                    break;
                }
            }
            ans[i]=sum;//把每个能爬到最高楼层依次存到数组中
        }
      
        
     
     for(int i=1;i<=q;i++)
    {int l=1,r=q;
        int mid; 
	  while(l<=r)
     {
          mid=(l+r)/2;
         if(b[mid]>k[i])
         {
             r=mid-1;
         }
         else if(b[mid]<k[i])
         {
             l=mid+1;
         }
         else
         break;
     }
     cout<<ans[mid]<<" ";
	 }
     cout<<endl;
    }
}