根式化简的多种奇妙解法

 弱者的第一篇博客

题目描述：

 

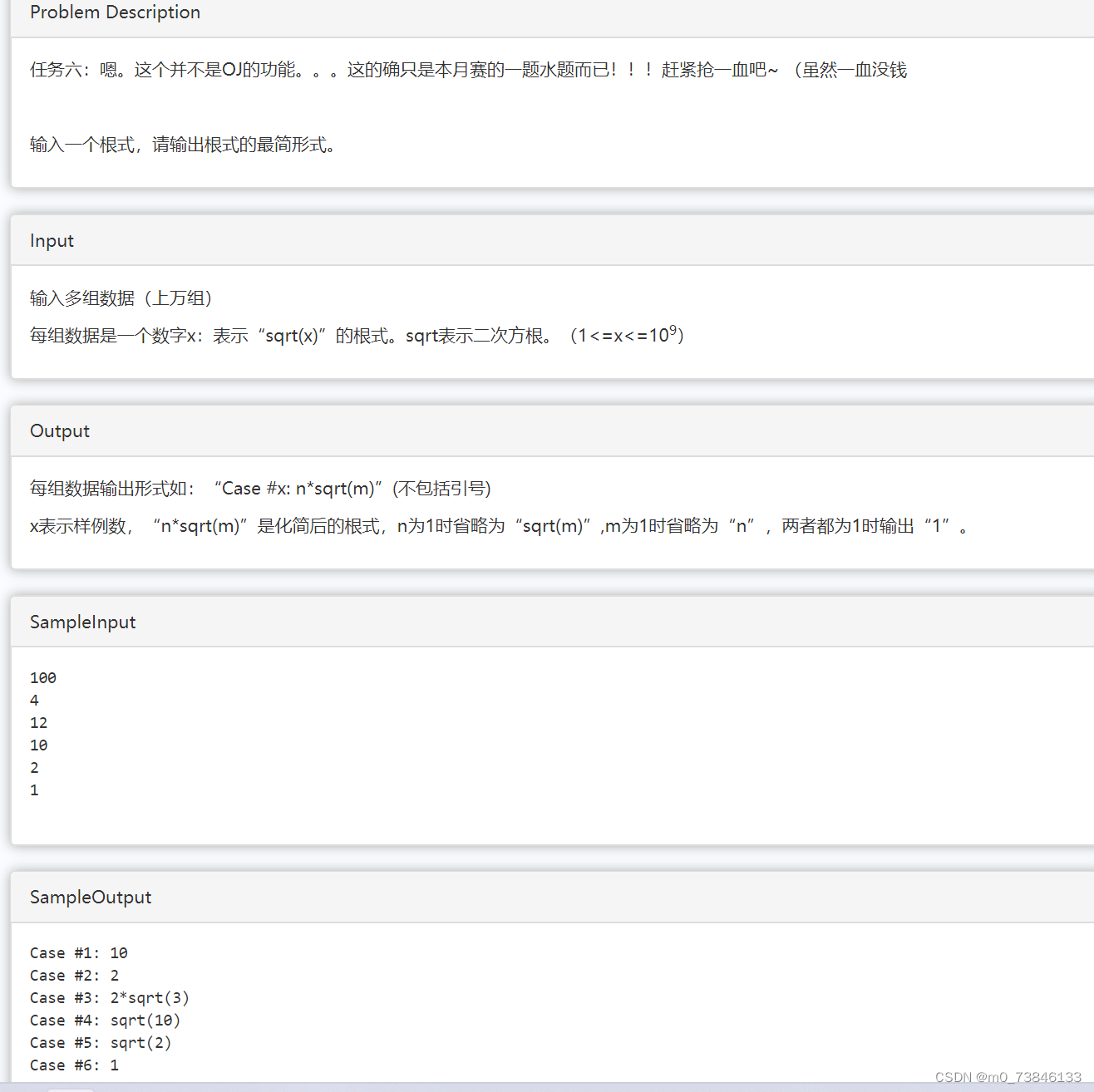
解法 1：

（弱者初学c时想到的代码，时间复杂度较高）

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <stdlib.h>
#include<iostream>
#include<string.h>
#include<cmath>
#include <algorithm>
#include<math.h>


using namespace std;
int main()
{
	long long a, c = 0, b;
	long long t = 1, h = 1;
	while (scanf("%lld", &a) != EOF)

	{
		for (b = 1; b * b <= a; b++)
		{
			long long q = b * b;//逐一枚举每个小于sqrt（a）的数，去寻找符合的值；
			if (a % q == 0)
			{
				t = b;
				h = a / q;//因数是对衬的因此可以通过小的数去找大的因数，减少时间复杂度；
			}
		}
		c++;
		if (h == 1)
		{
			printf("Case #%d: %d\n", c, t);
		}
		else if (t == 1)
		{
			printf("Case #%d: sqrt(%d)\n", c, a);
		}
		else
			printf("Case #%d: %d*sqrt(%d)\n", c, t, h);
	}
	return 0;
}

                                                                   解法2：

                               （弱者借来的代码，读书人的事不能叫偷（手动狗头））

解法1和解法2思想上大致相同；

#include<bits/stdc++.h>

using namespace std;

int main()
{
	int cnt = 1, x;
	while (cin >> x)
	{
		int a = sqrt(x);
		if (a * a == x)printf("Case #%d: %d\n", cnt++, a);
		else
		{
			while (x % (a * a) != 0)a--;//大体上解法1和解法2思想一致；
			if (a == 1)
			{
				printf("Case #%d: sqrt(%d)\n", cnt++, x);
			}
			else
			{
				printf("Case #%d: %d*sqrt(%d)\n", cnt++, a, x / (a * a));
			}
		}
	}

	return 0;
}

                                                                  解法3

   

（解法三是弱者初学c++，70天想到的奇妙解法，时间复杂度相对较低，但代码长度就另说）

可以想像成树：

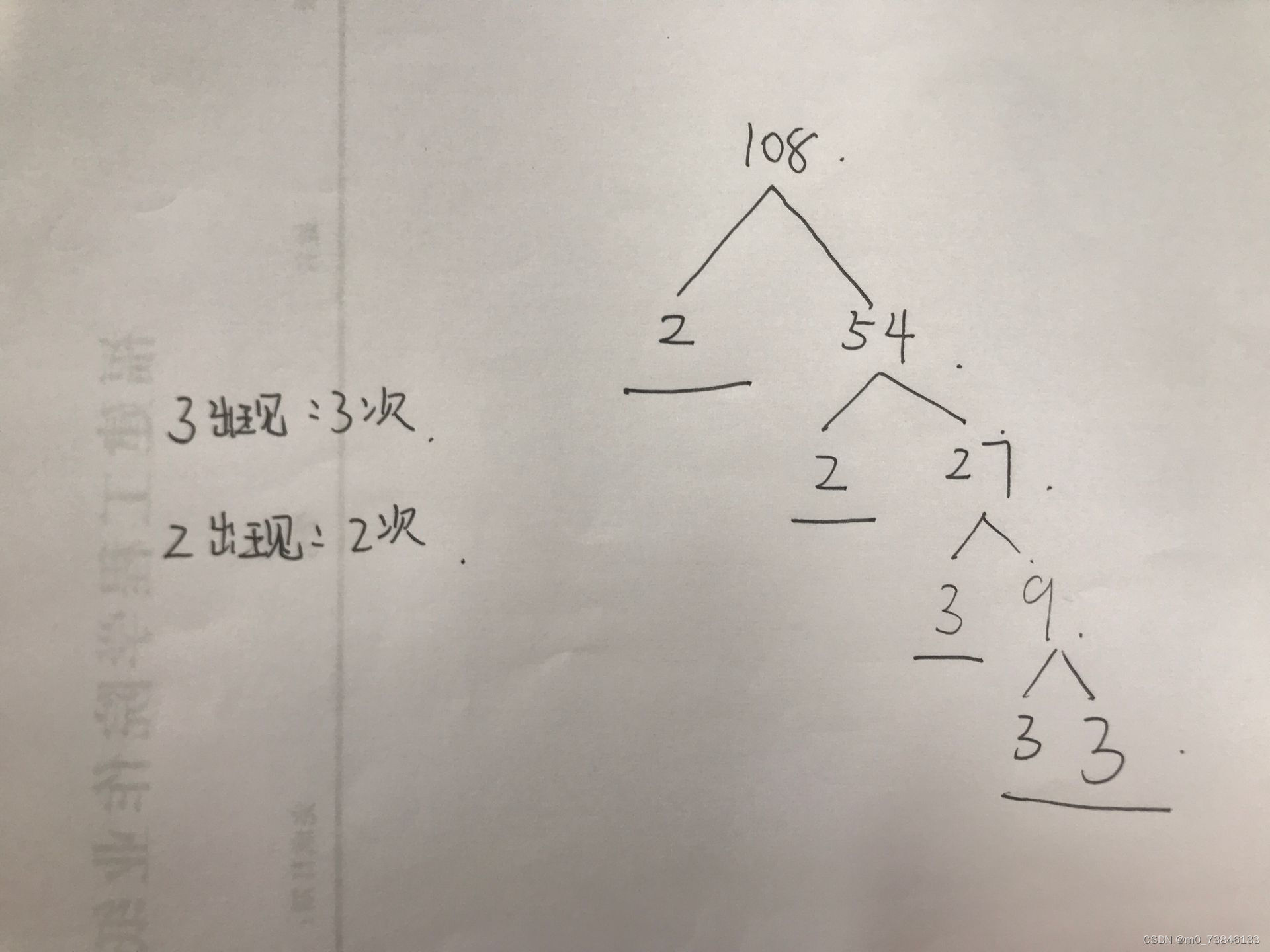
 我们所需要的是树的最底端各个数的值和数出现的次数

#define _CRT_SECURE_NO_WARNINGS 1
#include<bits/stdc++.h>
#include<iostream>
typedef long long ll;
using namespace std;
const int N = 32000;
ll x;
ll find(int x)//查找除1外的最小因数（作用：用于对映最大因数）
{
	ll ans=0;
	for (int i = 2; i * i <= x; i++)
	{
		if (x % i == 0)
		{
			ans = x / i;
		}
		if (ans != 0)return ans;
	}

	}
bool isprime(int n) {//素数判断
	if (n <= 1) return false;
	if (n == 2 || n == 3) return true;
	if (n % 6 != 1 && n % 6 != 5) return false;
	for (int i = 5; i * i <= n; i += 6) if (n % i == 0 || n % (i + 2) == 0) return false;
	return true;
}
struct cnm {
	ll ci;//储存小于sqrt（x）素数的个数
	ll su;//大于x的素数个数
};
void dg(ll a,cnm num[]) {
	ll b;
	int c;
	if (isprime(a) ) {
		if (a < sqrt(x))//使用sqrt（x）来降低时间复杂度，以及减少空间的使用，不然结构体数组炸了；
		{
			num[a].ci++;
		}
		else {
			num[x / a].su ++;
		}
	}
	else {
		c = find(a);
		b = a / c;
		dg(b,num);//递归去寻找
		dg(c, num);
	}

}

int main()
{
	
	
	ll i = 0;
		while(cin >> x)
		{
			i++;
			cnm num[N] = { 0 };
		ll a=1, b=1;
		if (isprime(x))printf("Case #%d: sqrt(%lld)\n", i, x);
		else {
			if ((ll)sqrt(x) * (ll)sqrt(x) == x)printf("Case #%d: %lld\n", i,(ll)sqrt(x));
			else {
				dg(x,num);
				for (int j = 1; j <=sqrt(x); j++)
				{
					if (num[j].ci >= 2||num[j].su>=2) {
						if (num[j]. ci >= 2)
						{
							for (int k = 1; k <= num[j].ci / 2; k++)//大于2个就可以去该素数的值
							{
								a = a * j;
							}
							num[j].ci = num[j].ci % 2;
						}
						if (num[j].su >= 2)
						{
							for (int k = 1; k <= num[j].su / 2; k++)
							{
								a = a * (x/j);
							}
							num[j].su = num[j].su % 2;
						}
					}
					if (num[j].ci >= 1||num[j].su>=1) {//只剩下一个的素数只能放在根号里面；
						if(num[j].ci>=1)
						  b = b * j;
						if (num[j].su >= 1)
							b = b * (x / j);
					}
				}
					if(a==1)
					printf("Case #%d: sqrt(%lld)\n", i, b);
					else 
				printf("Case #%d: %lld*sqrt(%lld)\n", i, a,b);
			}
		}

	}
}