离散数学及其应用--命题逻辑

命题逻辑

命题是一个陈述语句(即陈述事实的语句)，它或真或假，但不能既真又假。

命题变量(语句变量)：命题变量通常使用 p , q , r , s , … 等字母表示。

真值：真命题的真值为真，记为T或1,假命题的真值为F或0。

原子命题：不包含其他命题作为其组成部分的命题，即在结构上不能再分解出其他命题的命题.又称简单命题。原子命题不能带有非，或，且，如果，那么等联结词。

涉及命题的逻辑领域称为命题演算或命题逻辑。

复合命题：由已知命题用逻辑运算符组合而来的新命题。

联结词：

1.令p为一命题，则p的否定记作┑p，指"不是p所指的情形"。命题"┑p"读作"非p"。┑p的真值和p的真值相反。

2.令p和q为命题，p、q的合取即命题“p并且q”,记作p∧q，当p和q都是真时，p∧q命题为真，否则为假。

3.令p和q为命题，p和q的析取即命题"p或q"，记作pVq，当p和q均为假时，合取命题pVq为假，否则为真。

4.令p和q为命题，p和q的异或(记作p⊕q)是这样一个命题，当p和q恰好只有一个为真时命题为真，否则为假。

5.令p和q为命题，条件语句p→q是命题"如果p,则q"。当p为真而q为假时，条件语句p→q为假，否则为真。在条件语句p→q中，p称为假设(前件、前提)，q称为结论(后件)。

6.令p和q为命题，双条件语句p↔q是命题"p当且仅当q"。当p和q有同样的真值时，双条件语句为真，否则为假。双条件语句也称为双向蕴含。

逆命题、逆否命题与反命题

 由条件语句p→q可以构成一些新的条件语句。命题q→p称为p→q的逆命题，而p→q的逆否命题是命题┑q→┑p。命题┑p→┑q称为p→q的反命题。逆否命题总是和p→q具有相同的真值。

当两个复合命题总是具有相同真值时，无论其命题变量的真值是什么，我们称它们是等价的。因此一个条件语句与它的逆否命题是等价的。

双条件的隐式使用

在自然语言中双条件并不总是显式地使用。特别是在自然语言中很少使用双条件中的“当且仅当”结构。通常用“如果，那么”或“仅当”结构来表示双向蕴含。“当且仅当”的另一部分则是隐含的。也就是逆命题是蕴含的而没有明说出来。例如，考虑一下自然语言语句“如果你吃完饭了，则可以吃餐后甜点”。其真正含义是“你可以吃餐后甜点当且仅当你吃完饭”。后面这个语句在逻辑上等价于两个语句“如果你吃完饭，那么你可以吃甜点”和“仅当你吃完了饭，你才能吃甜点”。由于自然语言的这种不精确性，我们需要对自然语言中的条件语句是否隐含它的逆做出假设。因为数学和逻辑注重精确，所以我们总是区分条件语句p→q和双条件语句p↔q。

复合命题的真值表

 

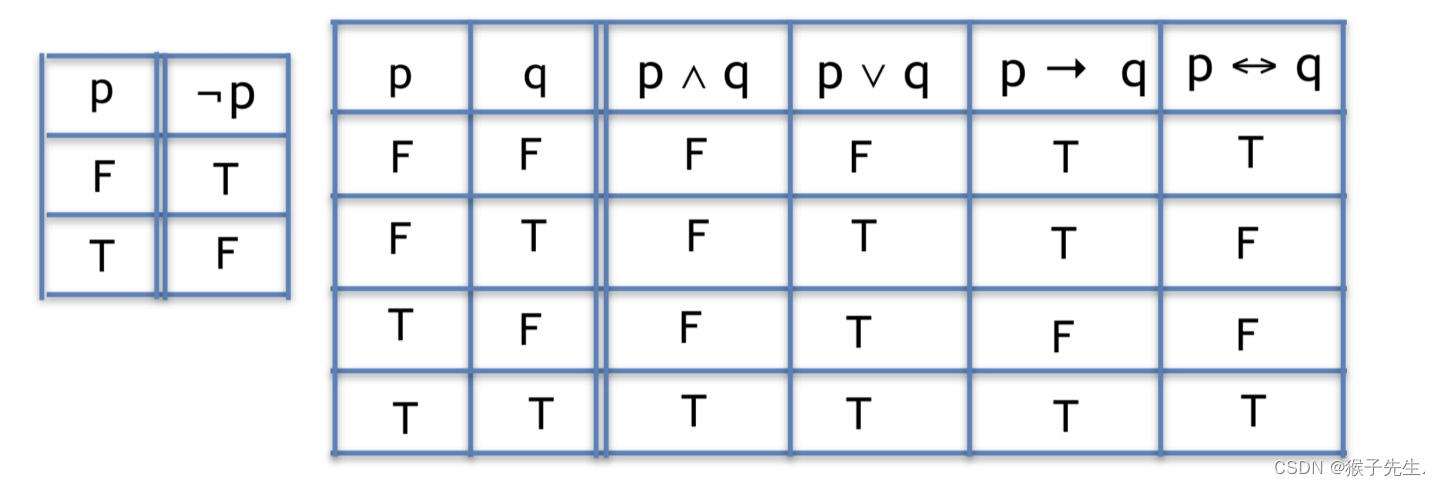
逻辑运算符的优先级

逻辑运算符若不加括号,先算非,再算与,然后是或,然后是→，最后是↔,即优先顺序是┑>∧>Ⅴ>→>↔。

比特运算

计算机用比特表示信息。比特是一个具有两个可能值的符号，即0和1。1表示真，0表示假。如果一个变量或为真或为假，则此变量就称为布尔变量。

计算机的比特运算（或位运算）对应于逻辑联结词。只要在运算符∧、V和⊕的真值表中用1代替T，用0代替F，我们还会用符号OR、AND和XOR分别表示运算符V、∧和⊕，许多程序设计语言正是这样表示的。

 

比特串是0比特或多比特的序列。比特串的长度就是它所含比特的数目。