算法学习07:KMP算法(字符串匹配)
前言

要记忆的模版:
// 求next数组的过程:(还是不太明白为什么可以求出来!!!)
// j:表示匹配成功的位数
for(int i = 2, j = 0; i <= n; i ++)
{
// 推无可退、下一位匹配成功
while(j && p[i] != p[j + 1]) j = ne[j];
if(p[i] == p[j + 1]) j ++;
ne[i] = j;
}
// kmp 匹配过程:
for(int i = 1, j = 0; i <= m; i ++)
{
while(j && s[i] != p[j + 1]) j = ne[j];
if(s[i] = p[j + 1]) j ++;
//匹配成功:
if(j == n)
{
printf("%d", i - n + 1);
j = ne[j];//匹配成功,去寻找下一个子串
}
}
提示:以下是本篇文章正文内容:
一、KMP算法
1.kmp匹配过程:
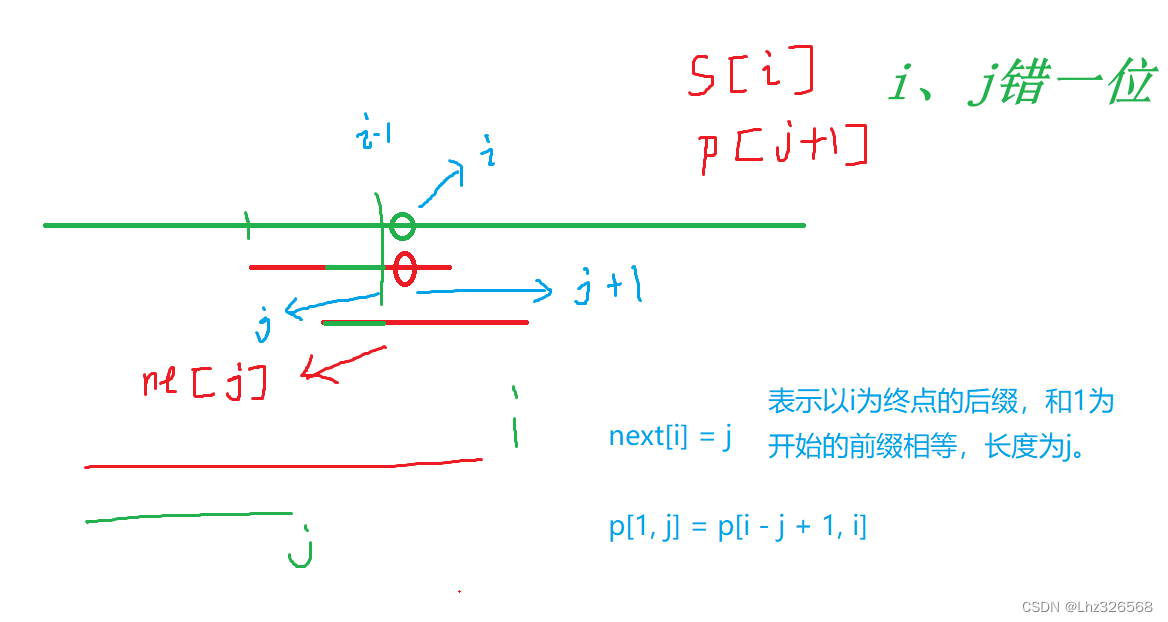
2.求解next数组(kmp算法重点)

3.代码
#include <iostream>
using namespace std;
const int N = 10000 + 10, m = 100000 + 10;
int n, m;
int p[N], s[N];//p:模版串, s:模式串
int ne[N]; //ne:next数组,表示 最少前进几步,后缀和前缀可以匹配
int main()
{
//s + 1:表示模式串 从索引1 开始 (看自己的习惯)
cin >> n >> p + 1 >> m >> s + 1;
// 求next数组的过程:
// j:表示匹配成功的位数
for(int i = 2, j = 0; i <= n; i ++)
{
// 推无可退、下一位匹配成功
while(j && p[i] != p[j + 1]) j = ne[j];
if(p[i] == p[j + 1]) j ++;
ne[i] = j;
}
// kmp 匹配过程:
for(int i = 1, j = 0; i <= m; i ++)
{
while(j && s[i] != p[j + 1]) j = ne[j];
if(s[i] = p[j + 1]) j ++;
//匹配成功:
if(j == n)
{
printf("%d", i - n + 1);
j = ne[j];//匹配成功,去寻找下一个子串
}
}
return 0;
}
总结
提示:这里对文章进行总结:
💕💕💕








 本文详细介绍了KMP算法,包括求解next数组的原理以及匹配过程的实现,通过代码示例展示了如何在模式串中使用KMP算法高效查找子串。
本文详细介绍了KMP算法,包括求解next数组的原理以及匹配过程的实现,通过代码示例展示了如何在模式串中使用KMP算法高效查找子串。















 427
427

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










