LeetCode-二分-搜索插入位置+搜索二维矩阵-CSDN博客

本文链接：https://blog.csdn.net/m0_74014989/article/details/148459041

LeetCode-二分-搜索插入位置

✏️ 关于专栏：专栏用于记录 prepare for the coding test。

文章目录

LeetCode-二分-搜索插入位置

📝 搜索插入位置

🎯题目描述

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

🔗题目链接：搜索插入位置

🔍 输入输出示例

示例 1:

输入: nums = [1,3,5,6], target = 5
输出: 2

示例 2:

输入: nums = [1,3,5,6], target = 2
输出: 1

示例 3:

输入: nums = [1,3,5,6], target = 7
输出: 4

🧩题目提示

1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 为 无重复元素 的升序排列数组
-104 <= target <= 104

🧪AC

本题的关键在于：

利用二分查找提高查找效率（时间复杂度要求为 O(log n)）。
当目标值存在时返回其索引，当目标值不存在时返回它将会插入的位置，也就是第一个大于等于 target 的位置。

left 代表搜索区间的起点；

right 代表搜索区间的终点；

循环中不断缩小区间，直到 left > right；

最终返回的 left 就是插入位置。

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int left = 0,right = nums.size() - 1;
        while(left <= right){
            int mid = left + (right - left) / 2;
            if(nums[mid] < target){
                left = mid + 1;
            }else{
                right = mid - 1;
            }
        }
        return left;
    }
};

📝 搜索二维矩阵

🎯题目描述

给你一个满足下述两条属性的 m x n 整数矩阵：

每行中的整数从左到右按非严格递增顺序排列。
每行的第一个整数大于前一行的最后一个整数。

给你一个整数 target ，如果 target 在矩阵中，返回 true ；否则，返回 false 。

🔗题目链接：搜索二维矩阵

🔍 输入输出示例

示例 1:

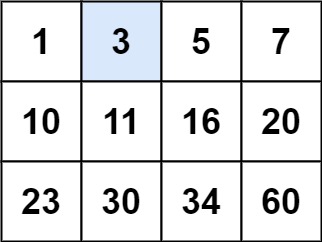
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true

示例 2:

输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出：false

🧩题目提示

m == matrix.length
n == matrix[i].length
1 <= m, n <= 100
-104 <= matrix[i][j], target <= 104

🧪AC

本质是一个升序的一维数组，只是按二维矩阵展开。

技巧：

将二维坐标 (i, j) 映射为一维下标：k = i * n + j
二分查找时反向映射：
```
row = mid / n, col = mid % n
```

这样我们就可以直接在矩阵上进行标准二分查找。

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m = matrix.size(), n = matrix[0].size();
        int left = -1, right = m * n;
        while (left + 1 < right) {
            int mid = left + (right - left) / 2;
            int x = matrix[mid / n][mid % n];
            if (x == target) {
                return true;
            }
            (x < target ? left : right) = mid;
        }
        return false;
    }
};

🌟 总结

题目	我的理解与核心思路	关键点总结	易错点 / 注意事项	代码核心逻辑
搜索插入位置	标准二分查找变形题，如果找不到目标，就返回它应当插入的位置（第一个 ≥ target 的位置）	- 二分查找时间复杂度 O(log n)- 返回的不是 -1，而是插入位置 `left`	- 要返回的是 left 而不是 mid- 注意区间左闭右闭，循环条件为 `left <= right`	二分查找 + 最终返回 `left`
搜索二维矩阵	把二维矩阵视作一个升序的一维数组来处理，依然可以套用二分查找	- 坐标映射：`mid -> (row = mid / n, col = mid % n)`- 时间复杂度 O(log mn)	- 注意一维映射后不能越界- `left` 初始为 -1 而不是 0，写法略特殊	映射坐标后直接用 mid 去访问 matrix 元素

二分查找常用模板

int binarySearch(vector<int>& nums, int target) {
    int left = 0, right = nums.size() - 1;
    while(left <= right) {
        int mid = left + (right - left) / 2;
        if(nums[mid] == target) return mid;
        else if(nums[mid] < target) left = mid + 1;
        else right = mid - 1;
    }
    return -1;
}

插入位置模板总结

// 返回第一个大于等于 target 的位置
int searchInsert(vector<int>& nums, int target) {
    int left = 0, right = nums.size();
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) left = mid + 1;
        else right = mid;
    }
    return left;
}