本文介绍了FloodFill算法和BFS在解决图形处理问题中的应用，如池塘计数、城堡问题和识别山峰与山谷。FloodFill能在线性时间复杂度内找到连通块，BFS用于寻找最小路径并避免栈溢出。通过实例展示了如何使用这些算法解决问题，并提供了相应的C++代码实现。
目录
Flood Fill 算法：可以在线性时间复杂度内，找到某个点所在的连通块
BFS特点：求最小，基迭代，不会爆栈
Flood Fill 算法：可以在线性时间复杂度内，找到某个点所在的连通块
池塘计数
农夫约翰有一片 N∗M 的矩形土地。
最近，由于降雨的原因，部分土地被水淹没了。
现在用一个字符矩阵来表示他的土地。
每个单元格内，如果包含雨水，则用”W”表示，如果不含雨水，则用”.”表示。
现在，约翰想知道他的土地中形成了多少片池塘。
每组相连的积水单元格集合可以看作是一片池塘。
每个单元格视为与其上、下、左、右、左上、右上、左下、右下八个邻近单元格相连。
请你输出共有多少片池塘，即矩阵中共有多少片相连的”W”块。
输入格式
第一行包含两个整数 N 和 M
接下来 N行，每行包含 M个字符，字符为”W”或”.”，用以表示矩形土地的积水状况，字符之间没有空格。
输出格式
输出一个整数，表示池塘数目。
数据范围
1≤N,M≤1000
输入样例：
10 12
W........WW.
.WWW.....WWW
....WW...WW.
.........WW.
.........W..
..W......W..
.W.W.....WW.
W.W.W.....W.
.W.W......W.
..W.......W.
输出样例：
3
#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
typedef pair<int,int>PII;
const int N=1010;
char str[N][N];
bool st[N][N];
int dx[8]={1,1,0,-1,-1,-1,0,1};
int dy[8]={0,1,1,1,0,-1,-1,-1};
void bfs(int x1,int y1)
{
queue<PII>q;
str[x1][y1]='.';
st[x1][y1]=1;
q.push({x1,y1});
while(q.size())
{
auto t=q.front();
q.pop();
int x=t.first,y=t.second;
for(int i=0;i<8;i++)
{
int x2=x+dx[i],y2=y+dy[i];
if(str[x2][y2]=='W'&&!st[x2][y2])
{
q.push({x2,y2});
str[x2][y2]='.';
st[x2][y2]=1;
}
}
}
}
int main()
{
int n,m;scanf("%d%d",&n,&m);
getchar();
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
cin>>str[i][j];
int num=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
if(str[i][j]=='W'&&!st[i][j])
{
bfs(i,j);
num++;
}
}
cout<<num<<endl;
}城堡问题
1 2 3 4 5 6 7
#############################
1 # | # | # | | #
#####---#####---#---#####---#
2 # # | # # # # #
#---#####---#####---#####---#
3 # | | # # # # #
#---#########---#####---#---#
4 # # | | | | # #
#############################
(图 1)
# = Wall
| = No wall
- = No wall
方向：上北下南左西右东。
图1是一个城堡的地形图。
请你编写一个程序，计算城堡一共有多少房间，最大的房间有多大。
城堡被分割成 m∗n个方格区域，每个方格区域可以有0~4面墙。
注意：墙体厚度忽略不计。
输入格式
第一行包含两个整数 m 和 n，分别表示城堡南北方向的长度和东西方向的长度。
接下来 m 行，每行包含 n 个整数，每个整数都表示平面图对应位置的方块的墙的特征。
每个方块中墙的特征由数字 P 来描述，我们用1表示西墙，2表示北墙，4表示东墙，8表示南墙，P 为该方块包含墙的数字之和。
例如，如果一个方块的 P 为3，则 3 = 1 + 2，该方块包含西墙和北墙。
城堡的内墙被计算两次，方块(1,1)的南墙同时也是方块(2,1)的北墙。
输入的数据保证城堡至少有两个房间。
输出格式
共两行，第一行输出房间总数，第二行输出最大房间的面积（方块数）。
数据范围
1≤m,n≤50
0≤P≤15
输入样例：
4 7
11 6 11 6 3 10 6
7 9 6 13 5 15 5
1 10 12 7 13 7 5
13 11 10 8 10 12 13
输出样例：
5
9
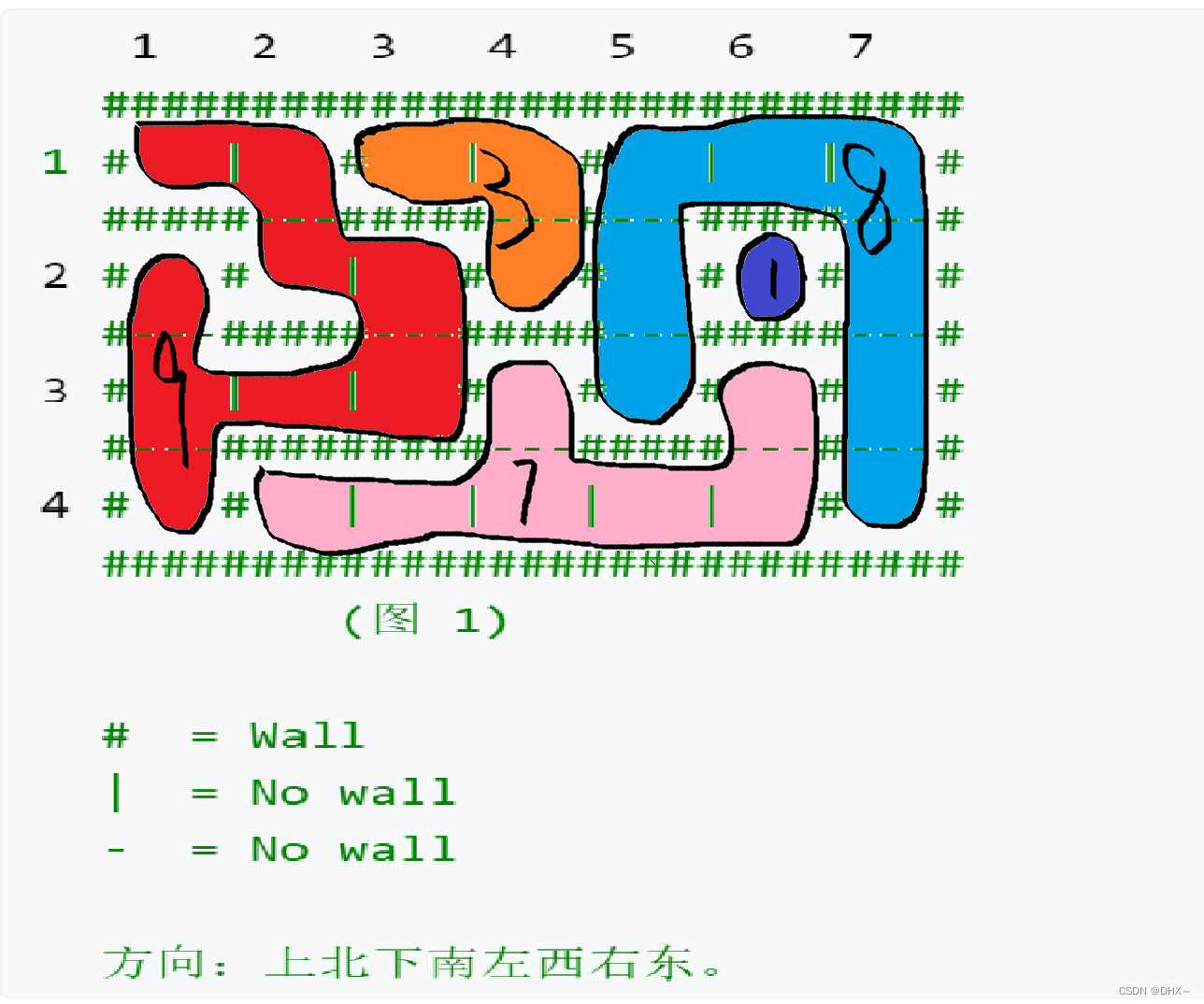
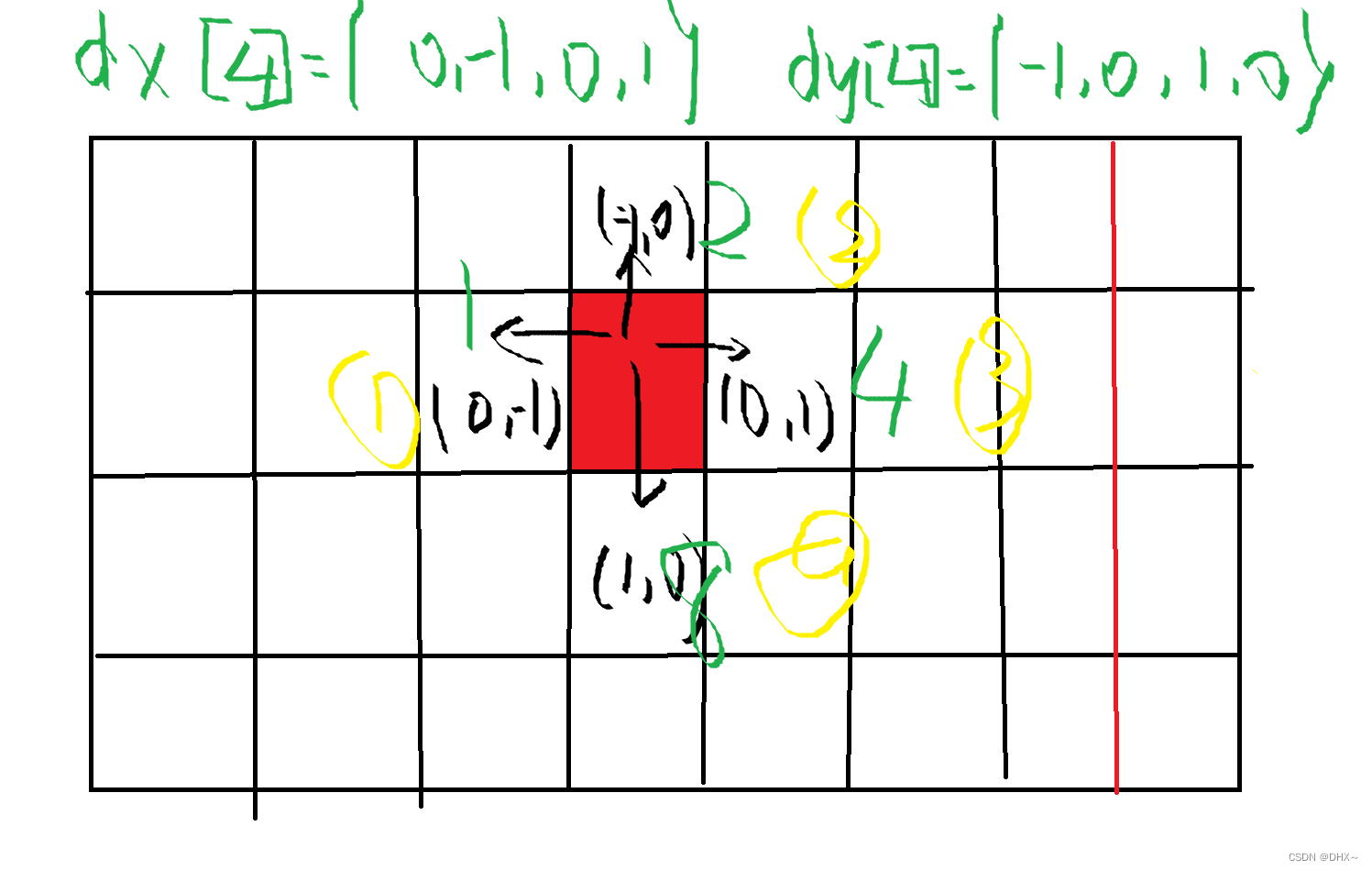
本题的关键用二进制&1表示是否有那面墙
#include<iostream>
#include<queue>
using namespace std;
const int N=55;
typedef pair<int,int>PII;
int a[N][N];
bool st[N][N];
int n,m;
//这个次序也很重要不能错了 要不就不能一一匹配了
int dx[4]={0,-1,0,1},dy[4]={-1,0,1,0};
int bfs(int x1,int y1)
{
st[x1][y1]=1;
queue<PII>q;
q.push({x1,y1});
int cnt=0;
while(q.size())
{
cnt++;
PII t=q.front();
q.pop();
int x2=t.first,y2=t.second;
for(int i=0;i<4;i++)
{
int x=x2+dx[i],y=y2+dy[i];
if(st[x][y]) continue;
if(x<1||x>n||y<1||y>m) continue;
//本题中最为关键的判断是否有墙，通过是否位运算 二进制去看
if((a[x2][y2]>>i)&1) continue;
st[x][y]=1;
q.push({x,y});
}
}
return cnt;
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++) cin>>a[i][j];
int cnt=0;
int max1=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(!st[i][j])
{
cnt++;
max1=max(max1,bfs(i,j));
}
cout<<cnt<<endl<<max1<<endl;
return 0;
}
山峰和山谷
FGD小朋友特别喜欢爬山，在爬山的时候他就在研究山峰和山谷。
为了能够对旅程有一个安排，他想知道山峰和山谷的数量。
给定一个地图，为FGD想要旅行的区域，地图被分为 n×n 的网格，每个格子 (i,j)的高度 w(i,j) 是给定
若两个格子有公共顶点，那么它们就是相邻的格子，如与 (i,j) 相邻的格子有(i−1,j−1),(i−1,j),(i−1,j+1),(i,j−1),(i,j+1),(i+1,j−1),(i+1,j),(i+1,j+1)
我们定义一个格子的集合 S 为山峰（山谷）当且仅当：
- S 的所有格子都有相同的高度。
- S 的所有格子都连通。
- 对于 s 属于 S，与 s 相邻的 s′ 不属于 S，都有 ws>ws′（山峰），或者 ws<ws′（山谷）。
- 如果周围不存在相邻区域，则同时将其视为山峰和山谷。
你的任务是，对于给定的地图，求出山峰和山谷的数量，如果所有格子都有相同的高度，那么整个地图即是山峰，又是山谷。
输入格式
第一行包含一个正整数 n，表示地图的大小。
接下来一个 n×n 的矩阵，表示地图上每个格子的高度 w。
输出格式
共一行，包含两个整数，表示山峰和山谷的数量。
数据范围
1≤n≤1000,
0≤w≤10^9
输入样例1：
5
8 8 8 7 7
7 7 8 8 7
7 7 7 7 7
7 8 8 7 8
7 8 8 8 8
输出样例1：
2 1
输入样例2：
5
5 7 8 3 1
5 5 7 6 6
6 6 6 2 8
5 7 2 5 8
7 1 0 1 7
输出样例2：
3 3
样例解释
样例1：
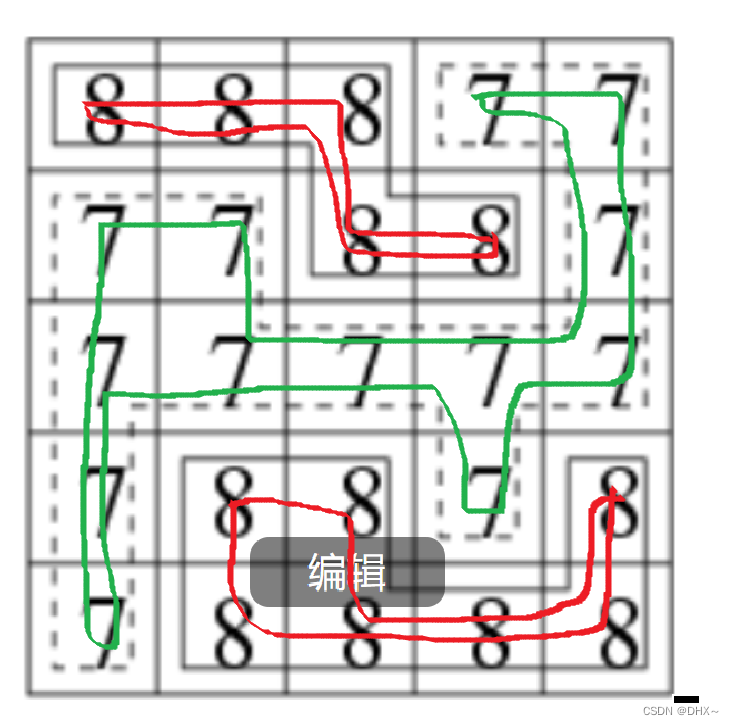
样例2：
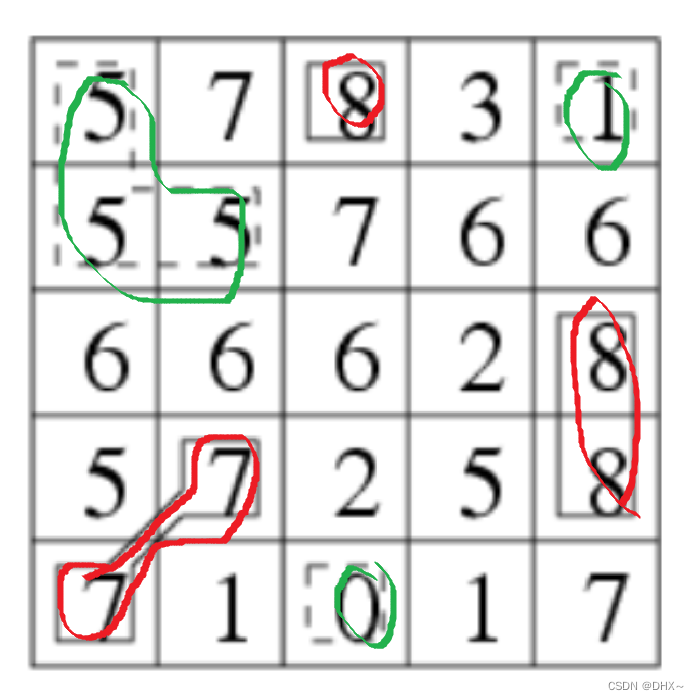
如果周围都比它低的话他就是山峰 如果周围都比它高的它就是山谷 如果高度都一样 它既是山谷又是山峰
#include<iostream>
#include<queue>
using namespace std;
const int N=1010;
typedef pair<int,int>PII;
int a[N][N];
bool st[N][N];
int n;
int flag,flag1;
int dx[8]={1,-1,0,0,1,1,-1,-1},dy[8]={0,0,-1,1,1,-1,1,-1};
void bfs(int x1,int y1)
{
queue<PII>q;
st[x1][y1]=1;
q.push({x1,y1});
int num=a[x1][y1];
while(q.size())
{
auto t=q.front();
q.pop();
int x2=t.first,y2=t.second;
for(int i=0;i<8;i++)
{
int x=x2+dx[i],y=y2+dy[i];
if(x<1||x>n||y<1||y>n) continue;
//这一步不能加 如果加了那他就不遍历了 就不知道这个num附近是否有比大还是小的数了
// if(st[x][y]) continue;
if(a[x][y]<num)
{
flag=1;
}
else if(a[x][y]>num)
{
flag1=1;
}
else if(a[x][y]==num&&!st[x][y])
{
q.push({x,y});
st[x][y]=1;
}
}
}
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++) cin>>a[i][j];
//num1山峰 num2山谷
int num1=0,num2=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
//flag山峰 有比num矮的数使flag=1 flag1山谷 有num大的数
flag=0;flag1=0;
if(!st[i][j])
{
bfs(i,j);
//num1山峰 num2山谷
if(flag&&flag1) continue;
if((flag&&!flag1)||(!flag&&!flag1)) num1++;
if((!flag&&flag1)||(!flag&&!flag1))num2++;
}
}
}
cout<<num1<<" "<<num2<<endl;
return 0;
}
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
