【C++】——AVL树（详细解读）

HackerElite

已于 2024-06-27 17:16:16 修改

阅读量787

点赞数 43

分类专栏：数据结构文章标签：数据结构

于 2024-06-27 17:15:47 首次发布

本文链接：https://blog.csdn.net/m0_74092462/article/details/140000387

版权

数据结构专栏收录该内容

6 篇文章 0 订阅

订阅专栏

3.确定平衡因子的改变，判断AVL树的改变

一 AVL树的概念

二叉搜索树虽可以缩短查找的效率，但如果数据有序或接近有序二叉搜索树将退化为单支树，查找元素相当于在顺序表中搜索元素，效率低下。

当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度。

它的左右子树都是AVL树
左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)

如果一棵二叉搜索树的高度是平衡的，它就是AVL树。如果它有n个结点，其高度可保持在O ( l o g N ) O(logN)O(logN)，搜索时间复杂度也是O ( l o g N ) O(logN)O(logN)。
因为他接近完全二叉树

二 AVL树节点的定义

对于AVL的定义来说首先我们肯定是模板，然后我们的结构为三叉链，同时我们还需要一个平衡因子去平衡高度

template<class K,class V>
struct AVLTreeNode
{
	AVLTreeNode<K, V>* _left;
	AVLTreeNode<K, V>* _right;
	AVLTreeNode<K, V>* _parent;//三叉链
	pair<K, V> _kv;
	int _bf; //平衡因子

	AVLTreeNode(const pair<K, V>& kv)//构造函数
		:_left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _kv(kv)
		, _bf(0)
	{}
};

三 AVL树的插入

注意，这里只是简单对AVL树的情况大概总结一下，细节还需要看下面的具体过程

1.先和搜索二叉树一样，去找插入的结点

2.插入的时候，需要更新平衡因子

3.确定平衡因子的改变，判断AVL树的改变

1找插入位置

待插入结点的key值比当前结点小就插入到该结点的左子树。
待插入结点的key值比当前结点大就插入到该结点的右子树。
待插入结点的key值与当前结点的key值相等就插入失败。

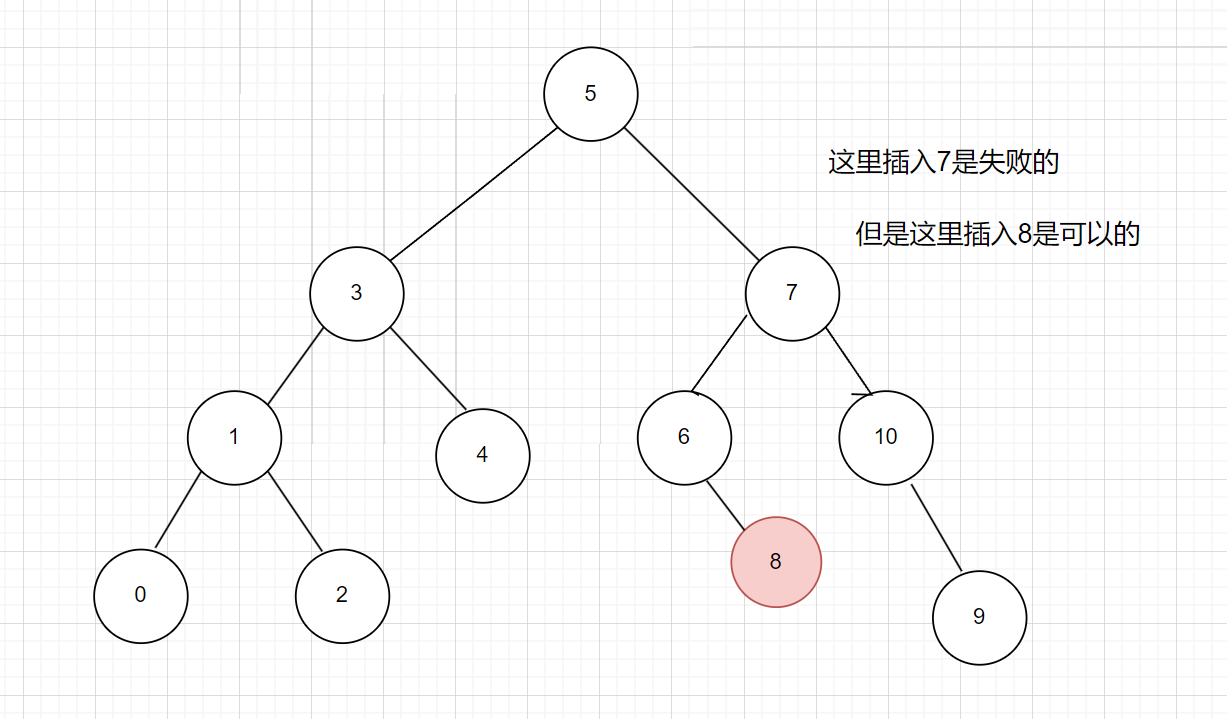
那这样我们根据上面的规则就很好写出我们的代码了

bool insert(const pair<K,V>& kv)
	{
		if (_root == nullptr)
		{
			_root = new Node(kv);
			return true;
		}
		Node* parent = nullptr;
		Node* cur = _root;
	
		while (cur)
		{
			if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_kv.first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}
		cur = new Node(kv);

2.更新平衡因子

我们插入可能会导致不平衡，这个时候我们就需要旋转去解决问题

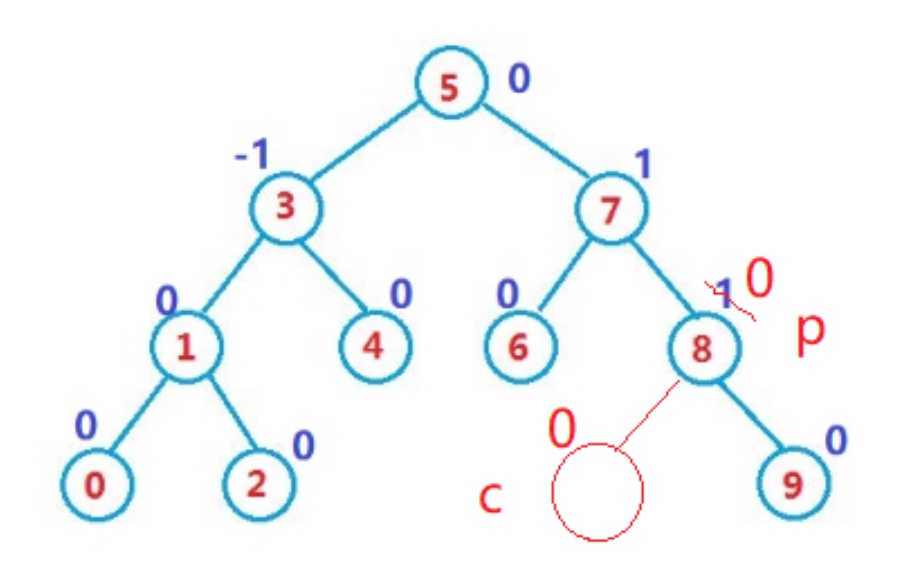
像上面的情况就不需要旋转去解决，因为子树的高度并没有变化，这里子树指的是 9

但是如果子树高度变化了，那么就需要去往上面更新

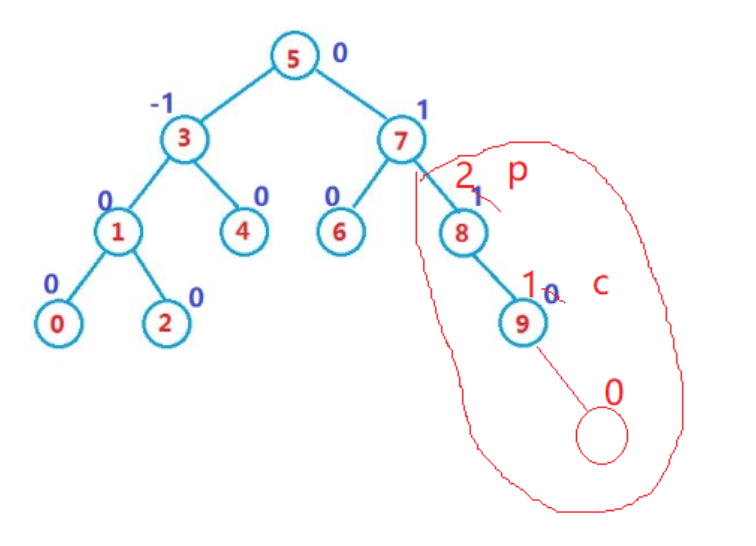
但是像上面这种，就会引发旋转，才能维持平衡，因为8的平衡因子为2已经破坏了平衡

1.父亲结点的平衡因子更新后为0,则不需要往上面更新

2.父亲结点的平衡因子更新后为1或者-1，则必须往上更新

3.父亲结点的平衡因子更新后为2或者-2，则需要旋转处理

3.判断AVL树的改变

如果父亲结点的平衡因子更新后为2或者-2，则需要旋转处理

到底要怎么旋转需要根据结点之间平衡因子的改变来判断

对于下面这种情况来说，在

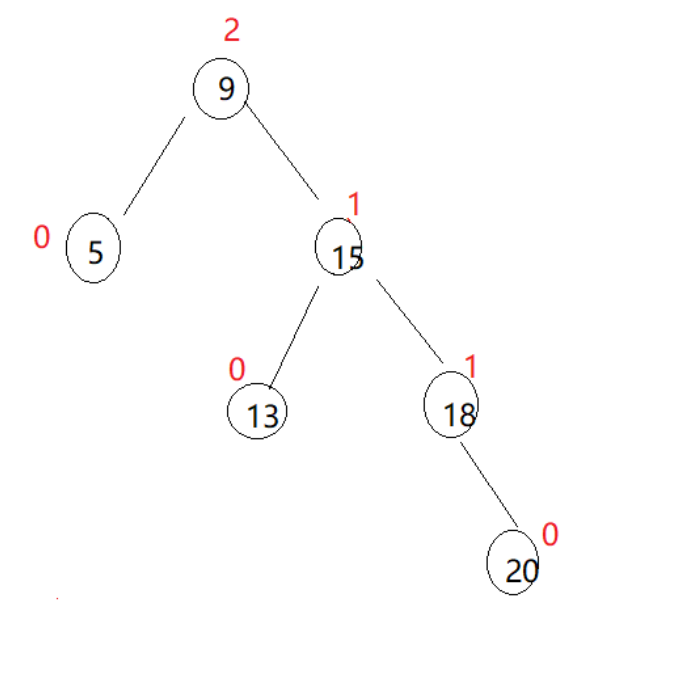
9 ：parent结点

15：cur结点

这里 parent的平衡因子为2，cur的平衡因子为1；

上图就是一个典型的左单旋，因为右边单纯高，左边单纯低，所以这里单纯的左单旋就行

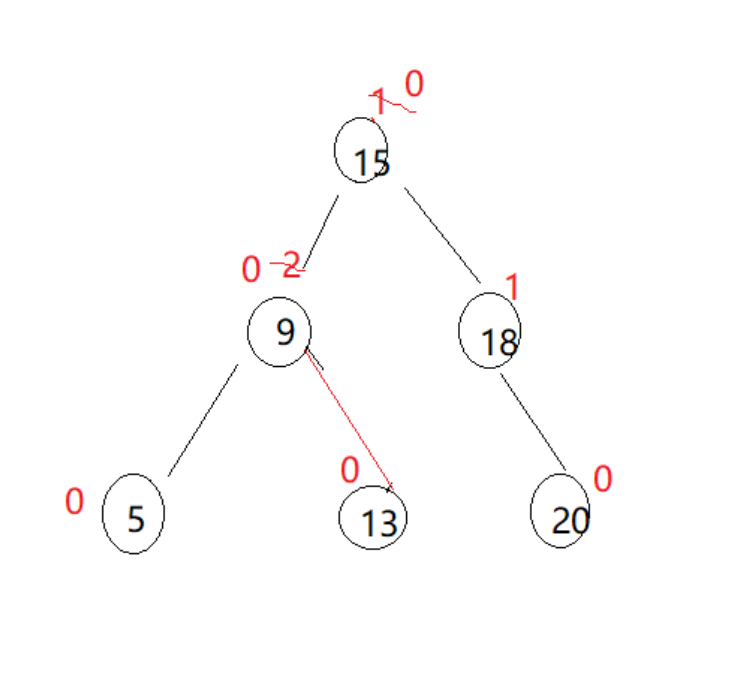
如果反过来就是一个右单旋

对右单旋来说就是parent的平衡因子为-2，cur的平衡因子为-1；

还有就是左右双旋和右左双旋

当parent的平衡因子为-2，cur的平衡因子为1时，进行左右双旋。
当parent的平衡因子为2，cur的平衡因子为-1时，进行右左双旋。

总结来说就是

当parent的平衡因子为-2，cur的平衡因子为-1时，进行右单旋。
当parent的平衡因子为-2，cur的平衡因子为1时，进行左右双旋。
当parent的平衡因子为2，cur的平衡因子为-1时，进行右左双旋。
当parent的平衡因子为2，cur的平衡因子为1时，进行左单旋。

三 AVL树的旋转

左单旋

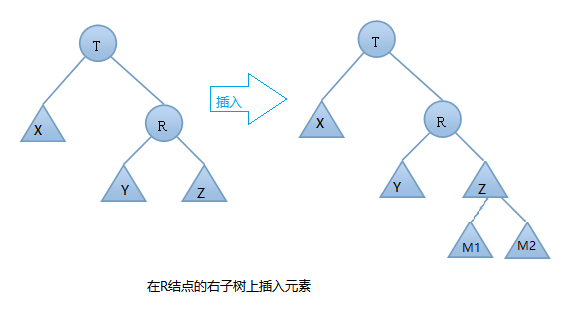
由上图可知：在插入之前树是一颗AVL树，而插入新结点之后，T的左右子树高度差的绝对值不再 < 1，此时AVL树的平衡性被破坏，我们要对其进行旋转。

左单旋步骤：

T向左旋转成为R的左结点
R的左节点Y放到T的右孩子上

根据上面的动图我们就可以很清楚去确定是怎么去操作的

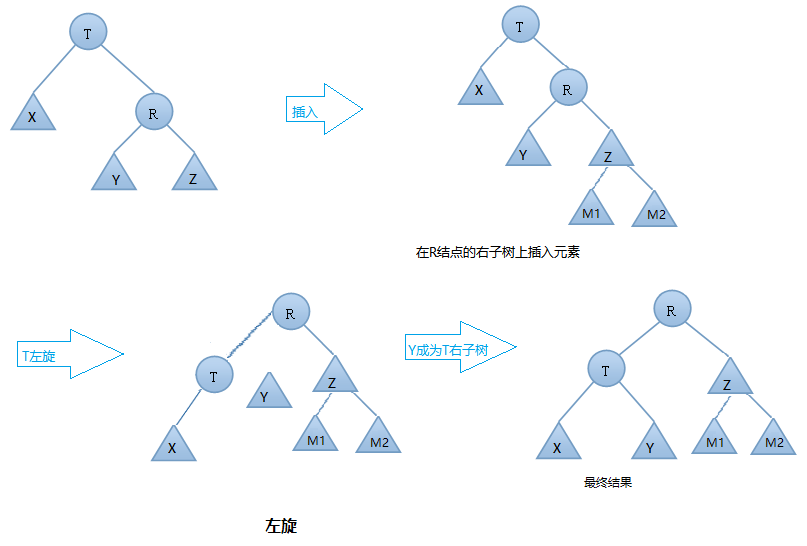
如果上面还是有点不理解，那么下面就看看抽象图

这里我们假设 30 为parent，60为subR, b为subRL

所有这里文字的解释就是

让subR的左子树作为parent的右子树。
让parent作为subR的左子树。
让subR作为整个子树的根。
更新平衡因子。

这里不用担心旋转以后会破化二叉搜索树的性质，因为：

subR的左子树当中结点的值本身就比parent的值大，因此可以作为parent的右子树。
parent及其左子树当中结点的值本身就比subR的值小，因此可以作为subR的左子树。

代码理解：

void RotateL(Node* parent)
	{
		Node* subR = parent->_right;//这里先进行旋转
		Node* subRL = subR->_left;

		parent->_right = subRL;//这里旋转已经完成，进行关系的变化
		subR->left = parent;

		Node* parentparent = parent->_parent;//可能这棵树只是一颗子树，所以要保留一下上一个结点
		parent->_parent = subR;
		if (subRL)//这里可能subRL是空，所以要特判
			subRL->_parent = parent;

		if (_root == parent)//如果是根那就不用parentparent了，直接变化关系就行
		{
			subR = _root;
			subR->_parent = nullptr;
		}
		else//如果不是根，只是一个子树，那就得看看是在parentparent的左还是右，再进行链接
		{
			if (parentparent->_left == parent)
			{
				parentparent->_left = subR;
			}
			else
			{
				parentparent->_right = subR;
			}
			subR->_parent = parentparent;
		}
		parent->_bf == subR->_bf = 0;//旋转完，平衡因子都是0
	}

右单旋

这里的右单旋就是和左单旋是一样的，只不过是方向变化了

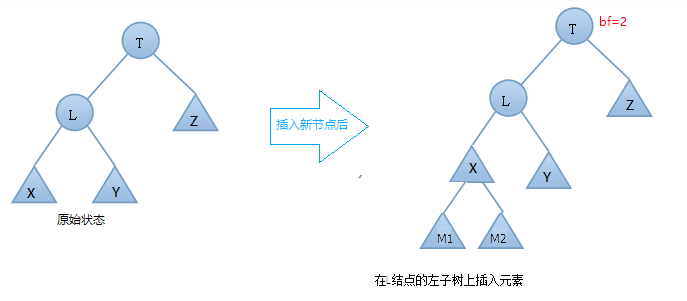
由上图可知：在插入之前树是一颗AVL树，而插入结点之后，T的左右子树高度差的绝对值不再 <= 1，此时AVL树的平衡性被破坏，我们要对其进行旋转。

又由于是左边高，导致的平衡因子异常，所以这里进行右单旋减低高度

右单旋步骤：

T向右旋转成为L的右结点
L的右节点Y 放到 T的左孩子上

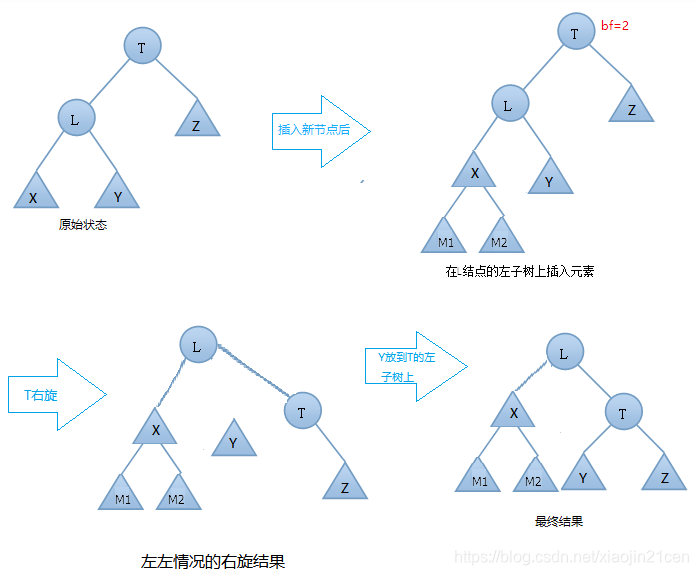
然后我们看看抽象图

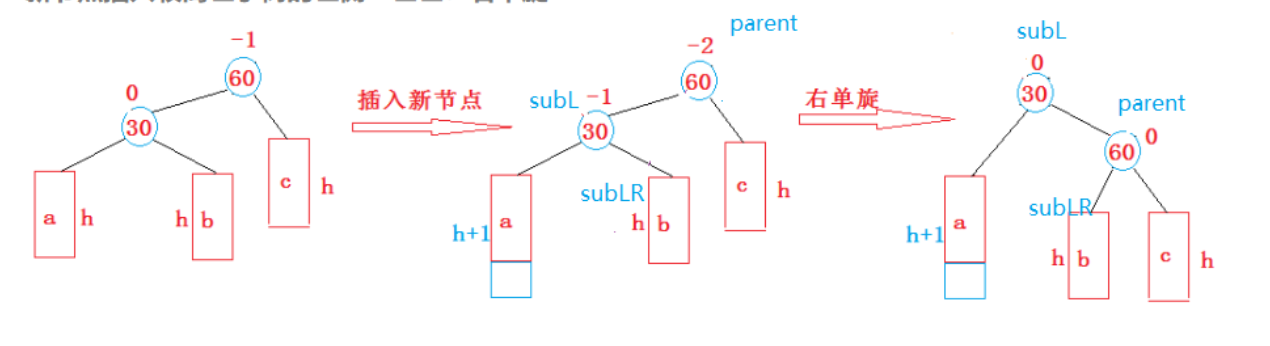
文字解释：

让subL的右子树作为parent的左子树。
让parent作为subL的右子树。
让subL作为整个子树的根。
更新平衡因子。

一样我们不用担心会破化二叉搜索树

subL的右子树当中结点的值本身就比parent的值小，因此可以作为parent的左子树。
parent及其右子树当中结点的值本身就比subL的值大，因此可以作为subL的右子树。

代码理解：

void RotateR(Node* parent)
	{
		Node* subL = parent->_left;//处理旋转
		Node* subLR = subL->_right;

		subL->_right = parent;//处理关系
		parent->_left = subLR;

		Node* parentparent = parent->_parent;//保留结点
		parent->_parent = subL;

		if (subLR)//特判
			subLR->_parent = parent;

		if (parent == _root)
		{
			subL = _root;
			subL->_parent = nullptr;
		}
		else
		{
			if (parentparent->_left == parent)
			{
				parentparent->_left = subL;
			}
			else
			{
				parentparent->_right = subL;
			}
			subL->_parent = parentparent;
		}
		parent->_bf = subL->_bf = 0;
	}

右左双旋

什么时候进行右左双旋呢？

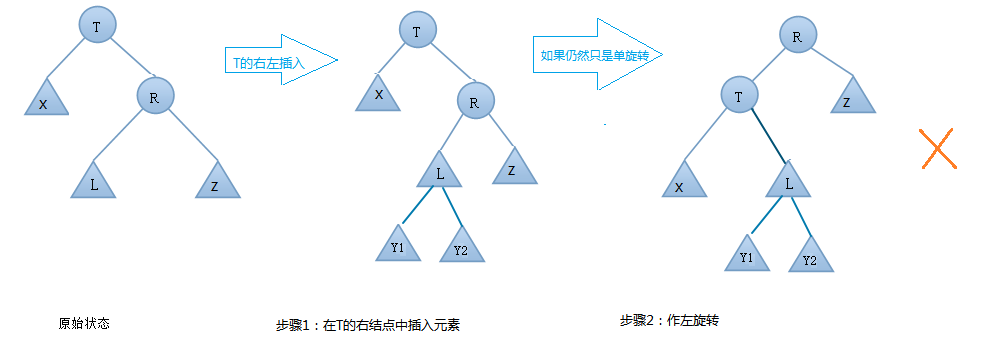
单纯的左旋解决不了问题（这里的左旋是左旋T），因为还是不平衡，所以这里需要进行右左双旋

但是注意这里的右左双旋是先右旋 R,再左旋T, 最后让L做根

第1次是右旋转：

R 节点右旋转，成为L的右节点
L的右节点（Y2）右旋转，成为R的左节点（即右子节点右转）

第2次是左旋转：

T 节点左旋转，成为L的左节点
L的左节点（Y1）左旋转，成为T的右节点（即左子节点左转）

抽象图就是

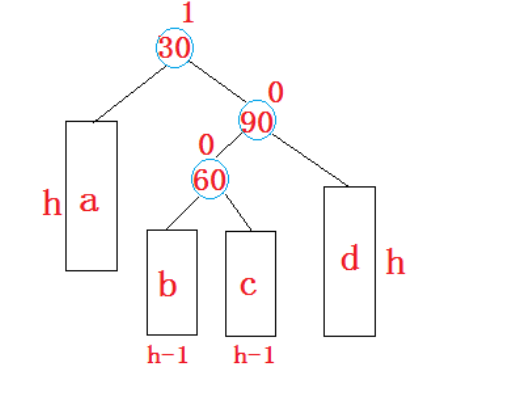
这是开始状态，当我们在b或者c差入的时候就引发了双旋

双旋后平衡因子改变

如果是在c位置插入，平衡因子的改变是不一样的

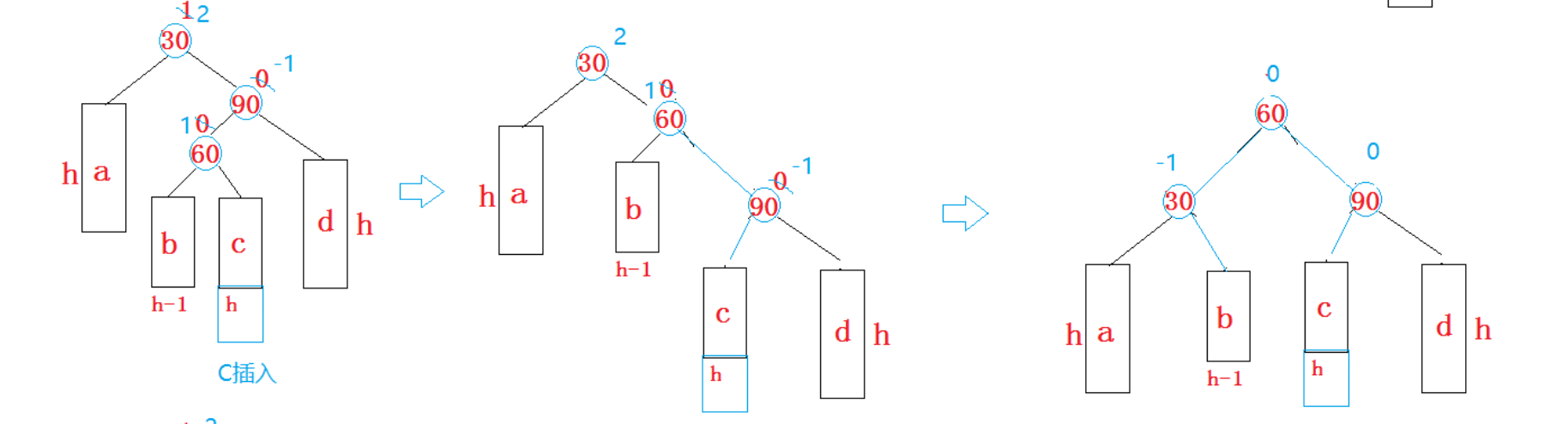
还有一种情况就是b,c是空，60这个结点就是新插入的结点

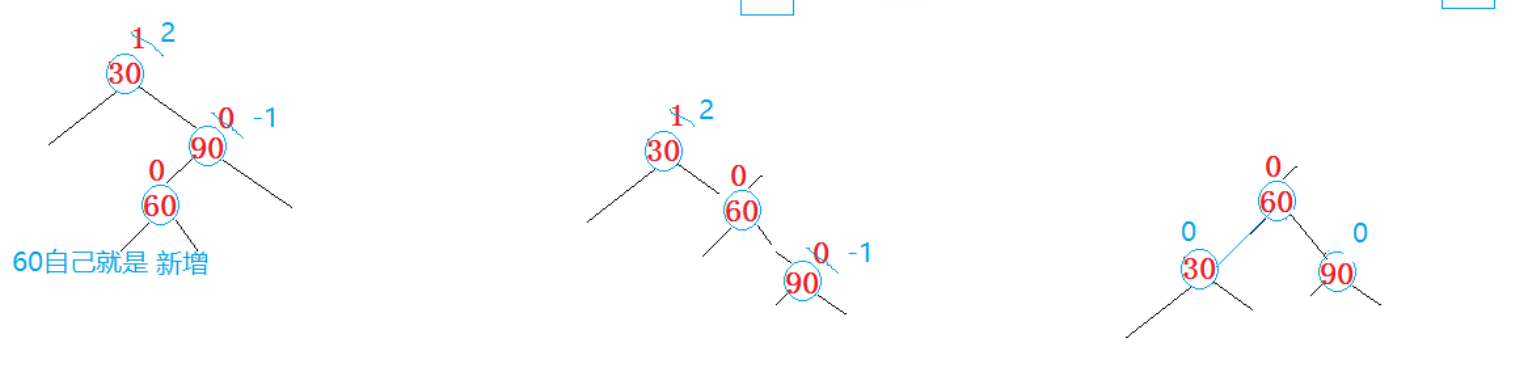
所以这里平衡因子的更新可以根据60 这个结点的平衡因子去判断最终所以平衡因子的改变

当 60 这个结点的平衡因子为-1的时候，那么旋转完 30：0 60：0 90：1；

当 60 这个结点的平衡因子为1的时候，那么旋转完 30：-1 60：0 90：0；

当 60 这个结点的平衡因子为0的时候，那么旋转完 30：0 60：0 90：0；

所以根据上面的结论我们很容易写出代码

其中

parent：30 ；

subR: 90;

subRL: 60;

void RotateRL(Node* parent)
	{
		Node* subR = parent->_right;//先确定变量
		Node* subRL = subR->_left;
		int bf = subRL->_bf;//平衡因子，后面需要用它去判断最终的变化

		RotateR(parent->_right);//先右旋
		RotateL(parent);//再左旋

		if (bf == 0)//按照上面总结的规律去更新平衡因子
		{
			parent->_bf = subR->_bf = subRL->_bf = 0;
		}
		else if (bf == -1)
		{
			parent->_bf = 0;
			subRL->_bf = 0;
			subR->_bf = 1;
		}
		else if (bf == 1)
		{
			parent->_bf = -1;
			subRL->_bf = 0;
			subR->_bf = 0;
		}
		else
		{
			assert(false);//如果不属于上面的情况，说明出了问题，直接断言掐死
		}
	}

左右双旋

什么时候进行左右双旋呢？

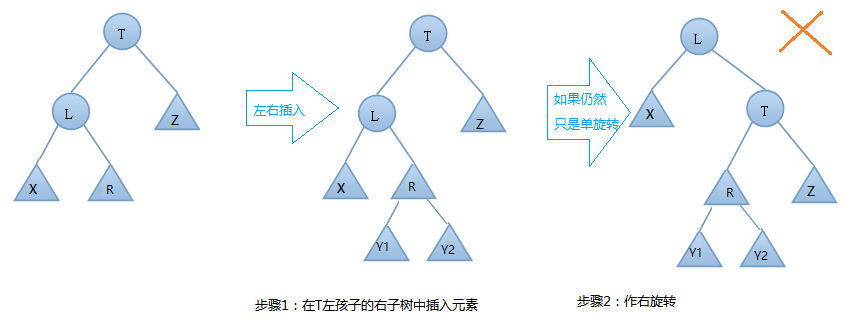
单纯的右旋解决不了问题（这里的右旋是右旋T），因为还是不平衡，所以这里需要进行左右双旋

但是注意这里的左右双旋是先左旋 L,再右旋T, 最后让R做根

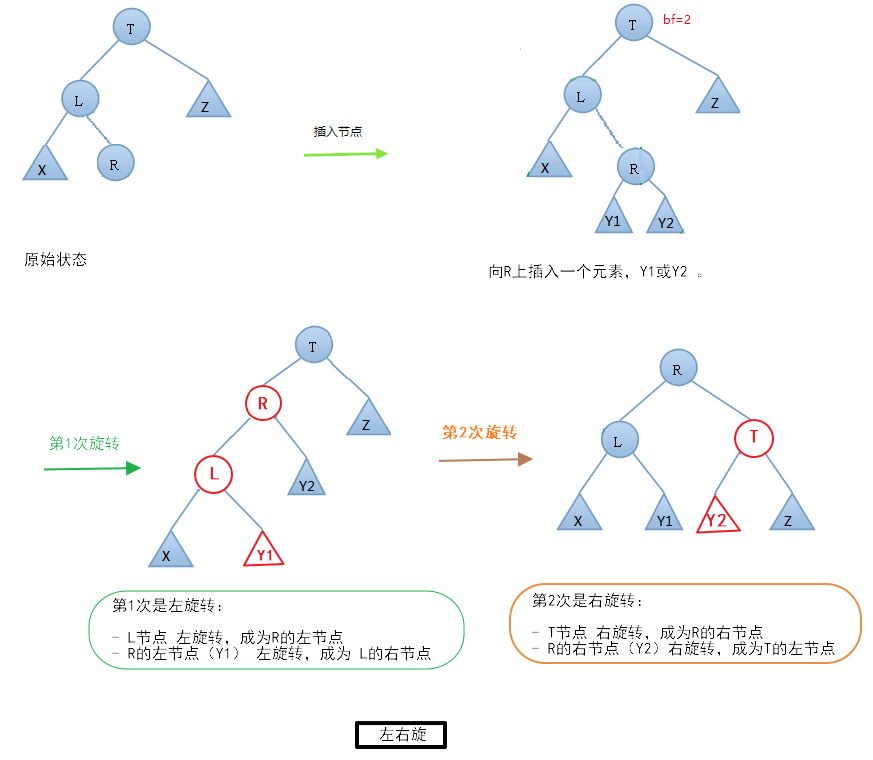
其实很容易发现它和右左双旋都一样，所以也分三种情况

当subLR原始平衡因子是-1时，左右双旋后parent、subL、subLR的平衡因子分别更新为1、0、0。

当subLR原始平衡因子是1时，左右双旋后parent、subL、subLR的平衡因子分别更新为0、-1、0。

当subLR原始平衡因子是0时，左右双旋后parent、subL、subLR的平衡因子分别更新为0、0、0。

所以我们也是根据平subLR的平衡因子不一样去处理的

代码理解

void RotateLR(Node* parent)
	{
		Node* subL = parent;//处理结点
		Node* subLR = subL->_right;
		int bf = subLR->_bf;//平衡因子

         //后面和右左双旋是一样的，只不过平衡因子变化有些不一样
		RotateL(parent->_left);
		RotateR(parent);
		if (bf == -1)
		{
			parent->_bf = 1;
			subLR->_bf = 0;
			subL->_bf = 0;
		}
		else if (bf == 1)
		{
			subLR->_bf = 0;
			subL->_bf = -1;
			parent->_bf = 0;
		}
		else if (bf == 0)
		{
			parent->_bf = 0;
			subL->_bf = 0;
			parent->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}

四 ALV插入完整代码

#pragma once
#include<assert.h>
template<class K,class V>
struct AVLTreeNode
{
	AVLTreeNode<K, V>* _left;
	AVLTreeNode<K, V>* _right;
	AVLTreeNode<K, V>* _parent;
	pair<K, V> _kv;
	int _bf; 

	AVLTreeNode(const pair<K, V>& kv)
		:_left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _kv(kv)
		, _bf(0)
	{}
};

template<class K,class V>
class AVLTree
{
	typedef AVLTreeNode<K, V> Node;
public:
	bool insert(const pair<K,V>& kv)
	{
		if (_root == nullptr)
		{
			_root = new Node(kv);
			return true;
		}
		Node* parent = nullptr;
		Node* cur = _root;
	
		while (cur)
		{
			if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_kv.first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}
		cur = new Node(kv);
		if (parent->_kv.first < kv.first)
		{
			parent->_right = cur;
			cur->_parent = parent;
		}
		else 
		{
			parent->_left = cur;
			cur->_parent=parent
		}
		while (parent)
		{
			if (cur == parent->_left)
			{
				parent->_bf--;
			}
			else
			{
				parent->_bf++;
			}
			if (parent->_bf == 0)
			{
				break;
			}
			else if (parent->_bf == 1 || parent->_bf == -1)
			{
				cur = parent;
				parent = parent->_parent;
			}
			else if (parent->_bf == 2 || parent_bf == -2)
			{
				//旋转
				if (parent->_bf == 2 && cur->_bf == 1)
				{
					RotateL(parent);
				}
				else if (parent->_bf == -2 && cur->_bf == -1)
				{
					RotateR(parent);
				}
				else if(parent->_bf == 2 && cur->_bf == -1)
				{
					RotateRL(parent);
				}
				else if (parent->_bf == -2 && cur->_bf == 1)
				{
					RotateLR(parent);
				}
				break;
			}
			else
			{
				assert(false);
			}

		 }
		 
		return true;
	}
	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		parent->_right = subRL;
		subR->left = parent;

		Node* parentparent = parent->_parent;
		parent->_parent = subR;
		if (subRL)
			subRL->_parent = parent;

		if (_root == parent)
		{
			subR = _root;
			subR->_parent = nullptr;
		}
		else
		{
			if (parentparent->_left == parent)
			{
				parentparent->_left = subR;
			}
			else
			{
				parentparent->_right = subR;
			}
			subR->_parent = parentparent;
		}
		parent->_bf == subR->_bf = 0;
	}

	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		subL->_right = parent;
		parent->_left = subLR;

		Node* parentparent = parent->_parent;
		parent->_parent = subL;

		if (subLR)
			subLR->_parent = parent;

		if (parent == _root)
		{
			subL = _root;
			subL->_parent = nullptr;
		}
		else
		{
			if (parentparent->_left == parent)
			{
				parentparent->_left = subL;
			}
			else
			{
				parentparent->_right = subL;
			}
			subL->_parent = parentparent;
		}
		parent->_bf = subL->_bf = 0;
	}

	void RotateRL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		int bf = subRL->_bf;

		RotateR(parent->_right);
		RotateL(parent);

		if (bf == 0)
		{
			parent->_bf = subR->_bf = subRL->_bf = 0;
		}
		else if (_bf == -1)
		{
			parent->_bf = 0;
			subRL->_bf = 0;
			subR->_bf = 1;
		}
		else if (_bf == 1)
		{
			parent->_bf = -1;
			subRL->_bf = 0;
			subR->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}

	void RotateLR(Node* parent)
	{
		Node* subL = parent;
		Node* subLR = subL->_right;
		int bf = subLR->_bf;


		RotateL(parent->_left);
		RotateR(parent);
		if (bf == -1)
		{
			parent->_bf = 1;
			subLR->_bf = 0;
			subL->_bf = 0;
		}
		else if (bf == 1)
		{
			subLR->_bf = 0;
			subL->_bf = -1;
			parent->_bf = 0;
		}
		else if (bf == 0)
		{
			parent->_bf = 0;
			subL->_bf = 0;
			parent->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}

private:
	Node* _root=nullptr;
};

五总结

插入位置	状态	操作
在parent的左结点（subL）的左子树（subL）上做了插入元素	左左型	右旋
在parent的左结点（subL）的右子树（subLR）上做了插入元素	左右型	左右旋
在parent的右结点（subR）的右子树（subR）上做了插入元素	右右型	左旋
在parent的右结点（subR）的左子树（subRL）上做了插入元素	右左型	右左旋

我们在AVL树插入元素的时候，肯定是先找的插入位置，然后插入，然后更新平衡因子，如果是子树变化导致父亲结点的平衡因子变为了 1 或者-1，那么就往上面继续更新，如果出现了2，-2则需要进行旋转，至于怎么旋转，则要看平衡因子之间的关系进行旋转（因为平衡因子体现了上面表格的具体情况），旋转完成也就是插入成功，同时也不需要再继续往上面更新了

HackerElite

关注

43
点赞
踩
26

收藏

觉得还不错? 一键收藏
18
评论
【C++】——AVL树（详细解读）

对于AVL的定义来说首先我们肯定是模板，然后我们的结构为三叉链，同时我们还需要一个平衡因子去平衡高度//三叉链int _bf;//平衡因子AVLTreeNode(const pair& kv)//构造函数, _kv(kv), _bf(0){}插入位置状态操作在parent的左结点（subL）的左子树（subL）上做了插入元素左左型右旋在parent的左结点（subL）的右子树（subLR）上做了插入元素左右型左右旋在parent的右结点（subR）的。
复制链接

扫一扫