快排系列1|快排简介

最新推荐文章于 2025-11-13 17:02:25 发布

原创最新推荐文章于 2025-11-13 17:02:25 发布 · 817 阅读

11 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #排序算法 #数据结构

快排思想

各版本思路介绍

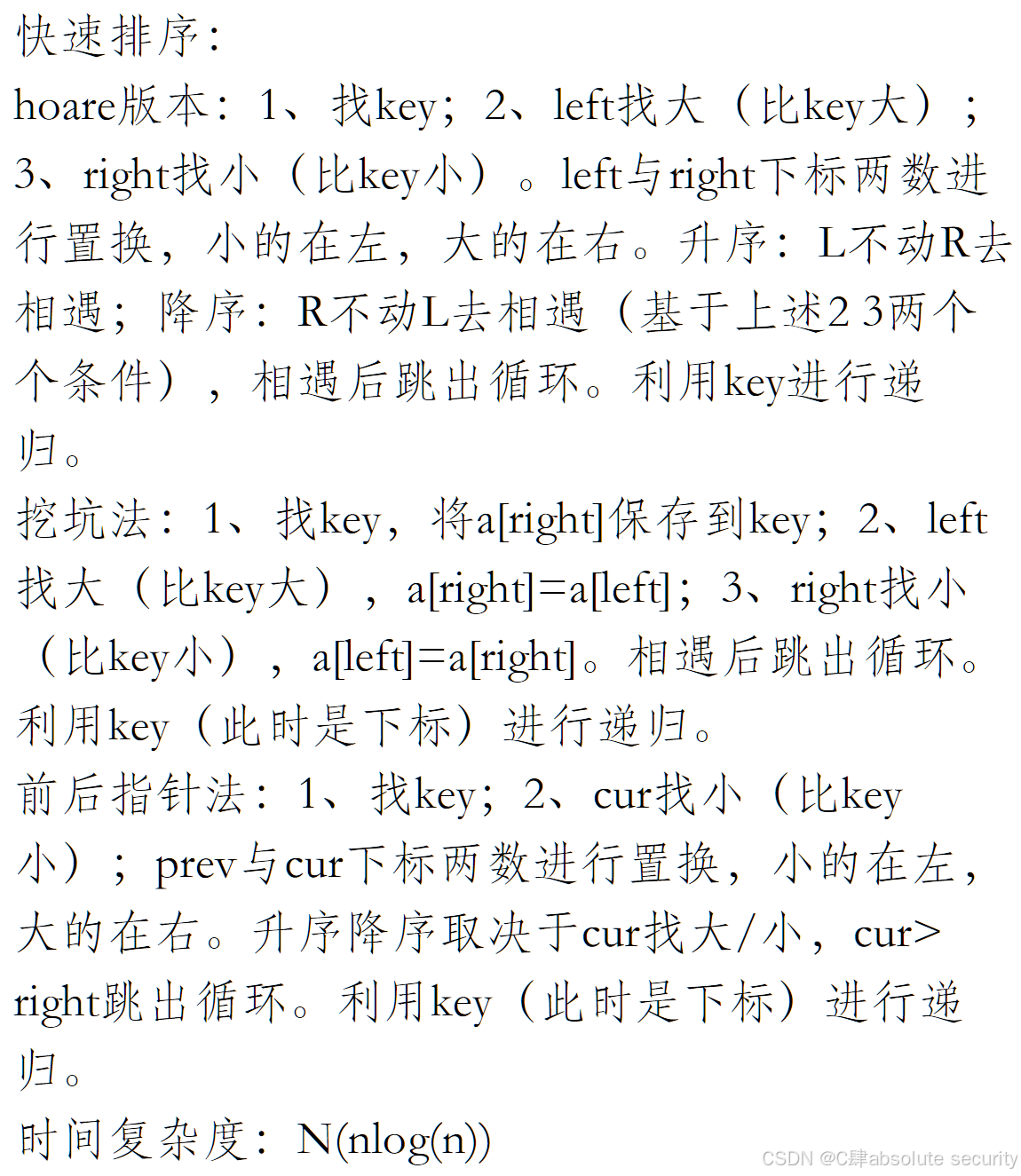
时间复杂度

最坏时间复杂度

当输入数组已经是有序或逆序时,每次选择的主元都是最大(最小)的元素,导致每次划分只能将数组分成一个空数组和一个含有 n-1个元素的数组,递归的深度为 n。此时每次划分的时间复杂度为 O(n)一共递归 n次,所以总时间复杂度为O(n^2)。

最优时间复杂度

当每次划分都能将数组均匀地划分为两个子数组时,递归的深度为 log n。此时每次划分的时间复杂度为 O(n),一共递归 logn次,所以总时间复杂度为O(n log n)。

空间复杂度

快速排序的空间复杂度通常被认为是 O(1)。
这是因为快速排序算法本身并不需要使用额外的线性空间来存储数据。它只需要一些常数级别的额外空间来存储一些辅助变量,如基准元素、左右指针等。
那么为什么上一个回答中说需要的额外空间是 O(log n)呢?这里主要是指递归调用过程中栈空间的占用。
在快速排序的递归实现中,每次递归调用时都需要将相关的变量压入调用栈中,等待返回后再弹出。由于递归深度为 O(log n),因此调用栈的深度也是 O(log n)。
所以,虽然快速排序本身不需要额外的线性空间,但由于递归调用需要使用栈空间,因此整个算法的额外空间复杂度为 O(log n)。

OJ题

基于随机抽样的快排

与下面前后指针法版本代码思路相同

前后指针法
遇到小的，cur++，prev++，不交换；
遇到大的，cur++，prev不++，再遇小，，prev++，在交换，大的在右，小的在左；
中间隔一个大的，再遇小的，才进行交换

（如图1-3）选取下标“r”元素为主元。

初始化：在循环第一轮迭代开始之前，i=j=p。此时p下标元素为“2”，仅满足第一个if条件，不进行交换，i++后，j++；

保持：当nums[j]<=nums[r]时，并i与j下标不相等，则进行交换nums[j] 和 nums[i]，再将i++，后j++，此时nums[i]<=nums[r]，而nums[j]>nums[r]；当nums[j+1]>nums[r]时，循环体唯一的操作是j++。根据循环不变量，被交换进nums[j]的值总是大于nums[r]。在每一次的迭代中存在两种可能的情况：（a）如果nums[j]<=nums[r]，需要做的便是j++，使循环不变量继续保持。（b）如果nums[j]>nums[r]，且i，j不相等（在同一个位置不交换），则交换nums[j]和nums[i]，将i++，再将j++。此时，循环不变量同样得到保持。

终止：当终止时，j=r。于是，数组中的每个元素都必然属于循环不变量所描述的三个集合的一个，也就是说，我们已经将数组中的所有元素划分成了三个集合：包含了所有小于等于nums[r]的元素的集合、包含了所有大于nums[r]的元素的集合和只有一个元素nums[r]的集合。

在此道oj题当中，使用快速排序，需要进行一些加工处理才能通过里面的测试案例，否则将会出现超时的报错（具体，家人们可以去尝试一下）。

快排的优化处理

三路划分

逻辑思路

遇到小的，cur向left交换，cur++，left++；
遇到大的，cur向right交换，right--；
相等的，cur++，直接过；
结束条件：c>r；
haore 和前后指针法的结合

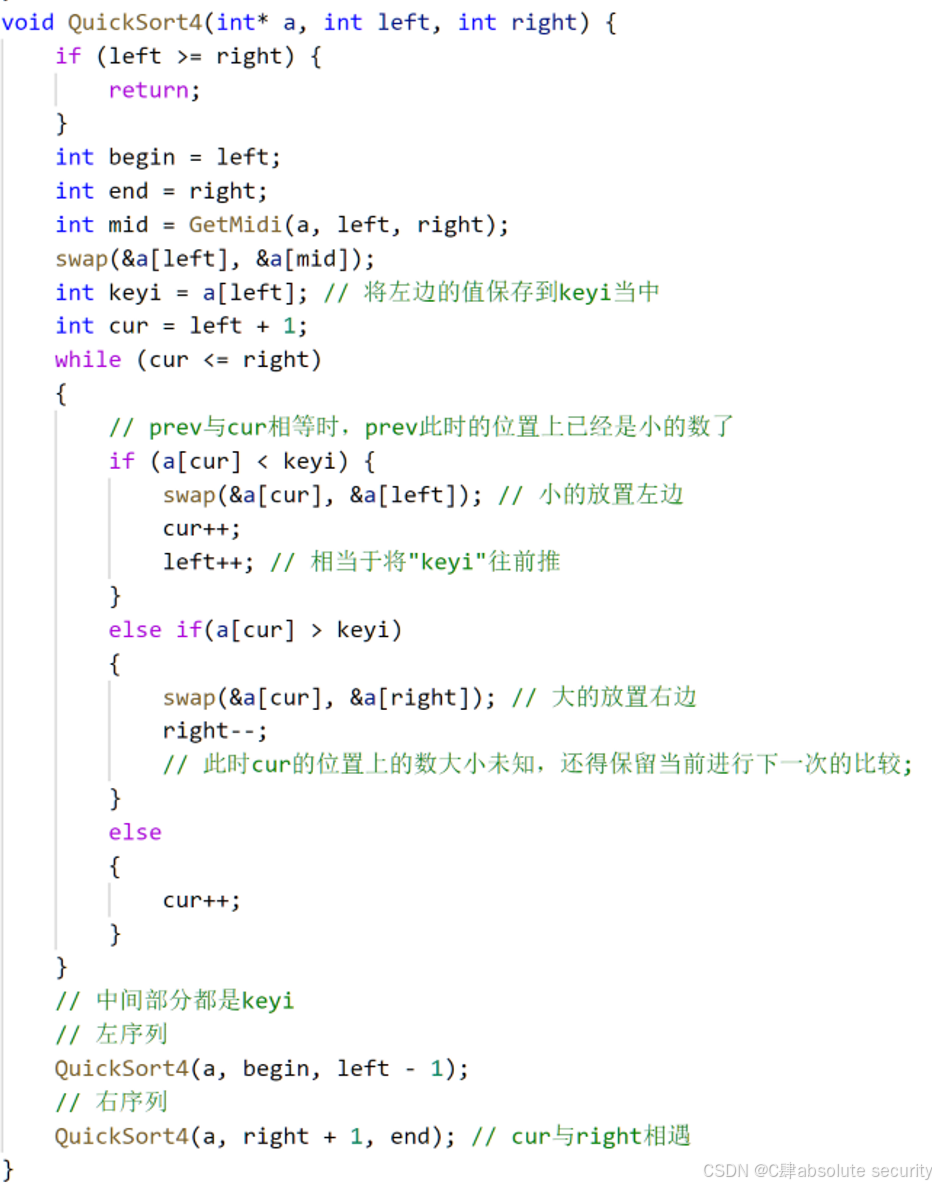
三路划分写法的特点

1.将数组分为三部分:小于基准值部分、等于基准值部分和大于基准值部分
2.使用三个指针:
left 指针指向小于基准值的部分的后一个元素。
cur 指针用于遍历数组。
right 指针指向大于基准值的部分的前一个元素。
3.算法流程:
选取基准值 a[left]。
初始化 left、cur、right 指针。
当 cur 指针小于等于 right 指针时，如果当前元素小于基准值，则与left 指针处的元素交换，并将 left指针前移。
如果当前元素大于基准值,则与right 指针处的元素交换,并将right 指针后移。
如果当前元素等于基准值,则 cur 指针前移。
4.递归处理左右两部分子数组,直到数组有序。

随机锚点

rand函数的使用

随机数范围:在给定范围「min，max]内，rand()%(max - min + 1)+ min 会均匀地生成每个可能的数值。由于 rand()生成的数是伪随机的，因此在一个足够大的运行次数下，范围内的每个数值都有可能出现。然而，短时间内或者次数较少时，可能会重复出现相同的数值。

代码部分

//Hoare版本
// 三数取中
int MidiGet(int* a, int left, int right)
{
	int midi = (right + left) / 2;
	if (a[left] < a[midi])
	{
		if (a[midi] > a[right])
		{
			return midi;
		}
		else if (a[left] < a[right])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
	else
	{
		if (a[midi] < a[right])
		{
			return midi;
		}
		else if (a[left] > a[right])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
}
// 快速排序hoare版本
int PartSort1(int* a, int left, int right)
{
	int mid = MidiGet(a, left, right);
	swap(&a[left], &a[mid]);
	int keyi = left;
	while (left < right)
	{
		//找大
		while (left <= right && a[left] <= a[keyi])
		{
			left++;
		}
		//找小
		while (left <= right && a[right] >= a[keyi])
		{
			right--;
		}
		//置换
		swap(&a[left], &a[right]);
	}
	swap(&a[left], &a[keyi]);
	return left;
}
void QuickSort1(int* a, int left, int right)
{
	if (left == right || left > right)
	{
		return;
	}
	int key = PartSort1(a, left, right);
	//左序列
	QuickSort1(a, 0, key - 1);
	//右序列
	QuickSort1(a, key + 1, right);
}

// 快速排序挖坑法
int PartSort2(int* a, int left, int right)//单趟排序
{
	int midi = MidiGet(a, left, right);
	//设定key值
	swap(&a[left], &a[midi]); 
	//设定key值
	int key =a[left];
	while (left < right)//跳出循环意味着相遇
	{
		//找小
		while (right > left && a[right] >= key)
		{
			right--;
		}
		a[left] = a[right];
		//找大;与key位置大小相同的，跳过
		while (left < right && a[left] <= key)
		{
			left++;
		}
		a[right] = a[left];

		//交换左右找到的数，保证小的在左边，大的在右边
		/*Swap(&a[left], &a[right]);*/
	}
	/*Swap(&a[key], &a[right]);*///比key小的变到最左边
	a[left] = key;
	return left;
}
void QuickSort2(int* a, int left, int right)
{
	if (left == right || left > right)
	{
		return;
	}
	int key = PartSort1(a, left, right);
	//左序列
	QuickSort2(a, 0, key - 1);
	//右序列
	QuickSort2(a, key + 1, right);
}

// 快速排序前后指针法
int PartSort3(int* a, int left, int right)
{
	int mid = MidiGet(a, left, right);
	swap(&a[left], &a[mid]);
	int keyi = left;
	int prev = left;
	int cur = prev + 1;
	while (cur <= right)
	{
		//prev与cur相等时，prev此时的位置上已经是小的数了
		if (a[cur] < a[keyi] && prev++ != cur)
		{
			swap(&a[cur], &a[prev]);
		}
		cur++;
	}
	swap(&a[prev], &a[keyi]);
	return prev;
}
void QuickSort3(int* a, int left, int right)
{
	if (left == right || left > right)
	{
		return;
	}
	int key = PartSort1(a, left, right);
	//左序列
	QuickSort3(a, 0, key - 1);
	//右序列
	QuickSort3(a, key+1, right);
}

参考：算法导论（第三版）；力扣题解