1. 属性数值化：将非数值属性转化为数学语言
想象你是一位厨师，正在为一道菜（机器学习模型）准备食材（数据）。有些食材是可以用数字直接表示的（数值属性），比如“甜度”；而有些食材是非数值的（非数值属性），比如“瓜类”。为了让计算机能够处理这些食材，你需要将它们转化为数学语言（数值化）。
1.1 有序属性的数值化
-
例子：甜度（高、中、低）是一个有序属性，因为“高 > 中 > 低”。
-
方法：你可以将“高”转化为 1.0，“中”转化为 0.5，“低”转化为 0.0。
-
结果：甜度从非数值属性变成了连续值，保留了相对大小关系。
1.2 无序属性的数值化
-
例子：瓜类（西瓜、南瓜、黄瓜）是一个无序属性，因为西瓜、南瓜、黄瓜之间没有明确的顺序关系。
-
方法：你可以将“瓜类”拆解为多个二元属性：
-
“是否是西瓜”：1 表示是，0 表示否。
-
“是否是南瓜”：1 表示是，0 表示否。
-
“是否是黄瓜”：1 表示是，0 表示否。
-
-
结果：每个样本的“瓜类”属性被转化为一个向量，比如：
-
西瓜：(1, 0, 0)
-
南瓜：(0, 1, 0)
-
黄瓜：(0, 0, 1)
-
2. 最优化问题：寻找最佳参数
想象你正在调整一道菜的配方（模型参数），目标是让这道菜的味道（目标函数）达到最佳。
2.1 目标函数
-
例子：目标函数是
，表示预测值与真实值之间的误差。 -
目标：找到参数 ww 和 bb，使得误差最小。
2.2 符号解释
-
min：表示求目标函数的最小值。比如，
表示求误差的最小值。 -
argmin：表示求使目标函数达到最小值的参数取值。比如，
表示找到使误差最小的 w 和 b。 -
s.t.：表示约束条件。比如，
表示在 w>0 且 b<0 的范围内，寻找使误差最小的 w 和 b。
1. 线性回归的目标：找到最佳拟合直线
想象你是一位园丁，正在种植一排植物（数据点）。你希望找到一条直线（线性模型），使得这条直线能够最好地拟合这些植物的生长趋势（数据分布）。这条直线的方程可以表示为：y=wx+by
其中：
-
y是植物的高度（目标值）。
-
x是植物的年龄（特征值）。
-
w 是斜率（权重），表示年龄对高度的影响。
-
b 是截距（偏置），表示植物在年龄为 0 时的初始高度。
你的目标是找到最佳的 w 和 b，使得这条直线与所有植物的高度误差最小。
2. 最小二乘法：最小化误差
为了找到最佳的 w和 b，你需要最小化所有植物的预测高度与实际高度之间的误差。这个误差可以用 均方误差（MSE） 来表示：
其中：
-
yi 是第 i 个植物的实际高度。
-
wxi+b是第 i个植物的预测高度。
-
m是植物的总数。
你的任务是通过调整 w和 b，使得 E(w,b)最小。
3. 推导过程：求解 w 和 b
3.1 对 w 求偏导
为了找到 E(w,b) 的最小值，你需要对 w和 b分别求偏导，并令偏导等于 0。
-
对 ww 求偏导：
令偏导等于 0：
3.2 对 b 求偏导
-
对 b 求偏导：
令偏导等于 0：
3.3 联立方程求解 ww 和 bb
通过联立上述两个方程，可以解得：
其中：
-
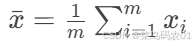是 x 的均值。 -
是 y 的均值。
4. 向量化：用矩阵运算加速计算
为了用计算机高效地计算 ww 和 bb，可以将上述公式向量化。设：
-
是去均值后的 xx。 -
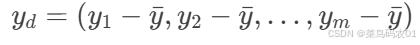是去均值后的 yy。
则 w 可以表示为：
5. 多元线性回归的推广
对于多元线性回归（多个特征），可以将 ww和 b 合并为一个向量
，并将输入特征扩展为 x^i=(xi;1)x^i=(xi;1)。此时，目标函数为：
通过矩阵运算，可以解得：
其中：
-
X 是输入特征矩阵。
-
y 是目标值向量。
tbc...
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
