计算机图形学之直线扫描转换算法：DDA（数字差分分析法）、Bresenham（布雷森汉姆算法）、中点算法（Midpoint Algorithm）实现QT图形绘制圆外接五角星、圆内接正方形、圆外切椭圆

于 2024-11-21 20:26:09 发布
阅读量982 收藏 11
点赞数 22
分类专栏： C++ 文章标签： 算法 c++ 计算机图形学 QT DAA 数字差分分析法 Bresenham 中点算法
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/m0_74334663/article/details/143953466
版权

直线扫描转换算法是一种将数学图形转换为像素的绘制算法，主要包括以下三种常见方法：

  1. DDA（数字差分分析法）
  2. Bresenham（布雷森汉姆算法）
  3. 中点算法（Midpoint Algorithm）
    绘制圆外接五角星、圆内接正方形、圆外切椭圆 的场景，这些图形分别可以与以下算法关联：
    文末附完整代码

1. 绘制圆外接五角星

相关算法：DDA 或 Bresenham（直线段）
  • 理由：
    五角星由多条直线段组成，直线扫描转换算法可以使用 DDA 或 Bresenham 来实现直线段的绘制。
    • DDA 算法：通过增量计算生成点坐标，效率较低，但逻辑简单。
    • Bresenham 算法：通过整数运算绘制直线，效率高且实现高效。
  • 适用场景：
    • 如果需要强调像素级别的性能优化（例如低分辨率的嵌入式设备），可以使用 Bresenham。
    • 在普通应用程序中，使用 Qt 提供的绘图方法（如 addPolygon）内部可能已优化为类似算法。
    •  // 使用DDA算法绘制直线
void Widget::drawLineDDA(QGraphicsScene *scene, int x1, int y1, int x2, int y2)
{
    int dx = x2 - x1;                       // 计算x方向的差
    int dy = y2 - y1;                       // 计算y方向的差
    int steps = std::max(abs(dx), abs(dy)); // 选择更大的方向进行扫描
    float xInc = dx / float(steps);         // 计算每步x的增量
    float yInc = dy / float(steps);         // 计算每步y的增量

    float x = x1, y = y1; // 设置起始点
    for (int i = 0; i <= steps; i++) {
        scene->addRect(x, y, 1, 1, QPen(Qt::black)); // 绘制一个像素点
        x += xInc;                                   // 更新x坐标
        y += yInc;                                   // 更新y坐标
    }
}
// 绘制圆外接五角星图像
void Widget::on_btn_drawStar_clicked()
{
    on_btn_clearDrawing_clicked();             // 清空当前绘制的图像
    const int points = 5;                      // 五角星有五个顶点
    double angleIncrement = 2 * M_PI / points; // 计算每个顶点的角度间隔
    double startAngle = -M_PI_2;               // 从顶部开始绘制五角星

    // 计算五角星顶点的坐标
    int starCoords[5][2];
    for (int i = 0; i < points; ++i)
     {
        double angle = startAngle + i * angleIncrement; // 计算当前顶点的角度
        starCoords[i][0] = x + radius * cos(angle);     // x 坐标
        starCoords[i][1] = y + radius * sin(angle);     // y 坐标
 	 }
	  // 按五角星的顶点连接顺序绘制线段
    for (int i = 0; i < points; ++i) 
    {
        int nextIndex = (i + 2) % points; // 跳过一个顶点连接（非相邻顶点）
        drawLineDDA(scene,
                    starCoords[i][0],
                    starCoords[i][1],
                    starCoords[nextIndex][0],
                    starCoords[nextIndex][1]); // 绘制线段
    }
    // 绘制外接圆
    scene->addEllipse(x - radius, y - radius, 2 * radius, 2 * radius, QPen(Qt::blue, 2));
}

在这里插入图片描述

2. 绘制圆内接正方形

相关算法：DDA 或 Bresenham（直线段）、中点圆算法
  • 理由：
    • 绘制内接正方形时：
      正方形由四条直线段构成，因此可以用 DDA 或 Bresenham 绘制。
    • 如果附带绘制圆：
      外接圆可以通过 中点圆算法 来实现高效的圆形扫描转换。
  • 适用场景：
    • 中点圆算法：
      它通过判断某一点与圆的误差函数关系（决策变量）确定圆周点，避免了复杂的浮点运算，非常高效。
    • Bresenham 直线算法：用于绘制正方形边界时效率较高。
    • // 使用中点圆算法绘制圆
while (x <= y) {
    plotCirclePoints(centerX, centerY, x, y); // 绘制八个对称点
    if (d < 0) {
        d += 2 * x + 3; // 如果判别值小于0，更新x，保持y不变
    } else {
        d += 2 * (x - y) + 5; // 如果判别值大于等于0，更新y，同时减少y
        y--;
    }
    x++; // 更新x坐标
 }
}
// 绘制圆内接正方形图像
void Widget::on_btn_drawRect_clicked()
{
    on_btn_clearDrawing_clicked();   // 清空当前绘制的图像
    int side = radius * sqrt(2) / 2; // 正方形的边长，使用勾股定理求得
    drawLineDDA(scene, x - side, y - side, x + side, y - side);                           // 上边
    drawLineDDA(scene, x + side, y - side, x + side, y + side);                           // 右边
    drawLineDDA(scene, x + side, y + side, x - side, y + side);                           // 下边
    drawLineDDA(scene, x - side, y + side, x - side, y - side);                           // 左边
    scene->addEllipse(x - radius, y - radius, 2 * radius, 2 * radius, QPen(Qt::blue, 2)); // 绘制外接圆
}

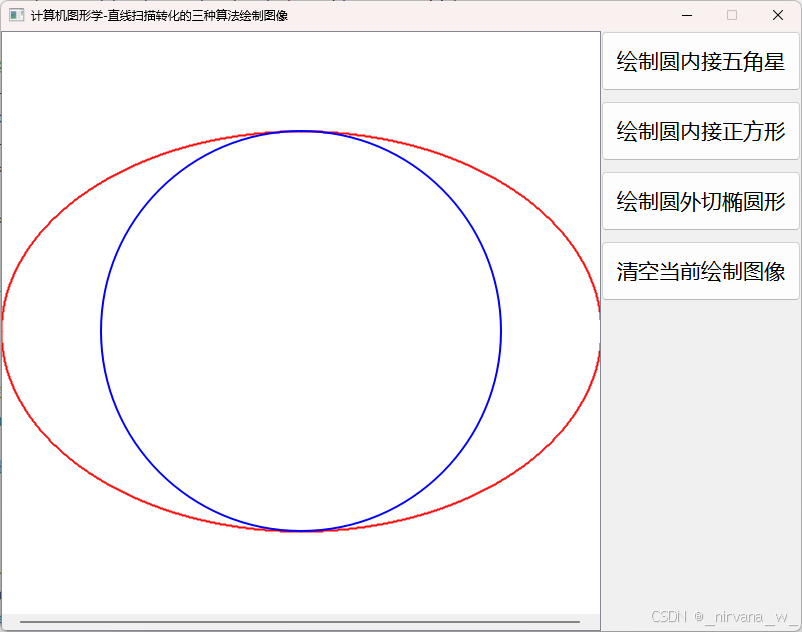
在这里插入图片描述

3. 绘制圆外切椭圆

相关算法：中点椭圆算法
  • 理由：
    • 绘制外切圆时可以使用 中点圆算法。
    • 椭圆本身可以通过 中点椭圆算法 来绘制，类似中点圆算法，使用决策变量判断椭圆的下一个像素点，分为两个区域（长轴区和短轴区）计算。
  • 适用场景：
    • 中点椭圆算法 是高效绘制椭圆的标准方法，避免了复杂的浮点运算。
    • 如果只是简单绘图（非像素级），Qt 的 addEllipse 方法可能已集成类似的优化。
    • // 使用中点椭圆算法绘制椭圆
void Widget::drawMidpointEllipse(QGraphicsScene *scene, int centerX, int centerY, int a, int b)
{
int x = 0, y = b;
double a2 = a * a, b2 = b * b;
double d = b2 - a2 * b + 0.25 * a2; // 初始判别值
// 绘制椭圆的对称点
auto plotEllipsePoints = [&](int cx, int cy, int x, int y)
 {
    scene->addRect(cx + x, cy + y, 1, 1, QPen(Qt::red));
    scene->addRect(cx - x, cy + y, 1, 1, QPen(Qt::red));
    scene->addRect(cx + x, cy - y, 1, 1, QPen(Qt::red));
    scene->addRect(cx - x, cy - y, 1, 1, QPen(Qt::red));
};
// 第一阶段：沿y轴递减
while (b2 * x <= a2 * y) 
{
    plotEllipsePoints(centerX, centerY, x, y); // 绘制四个对称点
    if (d < 0) 
    {
        d += b2 * (2 * x + 3); // 如果判别值小于0，更新x
    } else
     {
        d += b2 * (2 * x + 3) + a2 * (-2 * y + 2); // 如果判别值大于等于0，更新y并减少y
        y--;
    }
    x++; // 更新x坐标
}
    // 第二阶段：沿x轴递增
    d = b2 * (x + 0.5) * (x + 0.5) + a2 * (y - 1) * (y - 1) - a2 * b2;
    while (y >= 0)
     {
        plotEllipsePoints(centerX, centerY, x, y); // 绘制四个对称点
        if (d > 0)
         {
            d += a2 * (-2 * y + 3); // 如果判别值大于0，更新y
        } else {
            d += b2 * (2 * x + 2) + a2 * (-2 * y + 3); // 如果判别值小于等于0，更新x
            x++;
        }
        y--; // 更新y坐标
    }
}

在这里插入图片描述

总结

图形类型涉及算法说明
圆外接五角星DDA 或 Bresenham五角星由直线段构成，适合用直线扫描算法绘制。
圆内接正方形DDA 或 Bresenham + 中点圆算法正方形由直线构成，圆的绘制适合用中点圆算法。
圆外切椭圆中点椭圆算法椭圆外切圆的绘制适合使用中点圆算法和中点椭圆算法。

完整代码文件(3个文件)

main.cpp

#include "widget.h"
#include <QApplication>
int main(int argc, char *argv[])
{
    QApplication a(argc, argv);
    Widget w;
    w.show();
    return a.exec();
}

widget.h

#ifndef WIDGET_H
#define WIDGET_H

// 引入图形项类，用于图形场景的绘制
#include <QGraphicsEllipseItem>
#include <QGraphicsPolygonItem>
#include <QGraphicsScene>
// 引入鼠标滚轮事件类，用于缩放图像
#include <QWheelEvent>
// 引入QWidget类，用于创建GUI窗口
#include <QWidget>
// 引入数学库，用于数值计算
#include <math.h>

QT_BEGIN_NAMESPACE
namespace Ui {
class Widget; // 声明Widget类
}
QT_END_NAMESPACE

// 定义Widget类继承自QWidget类，表示图形窗口
class Widget : public QWidget
{
    Q_OBJECT // 必须定义Q_OBJECT宏，用于Qt的信号和槽机制

public:
    // 构造函数，初始化窗口，parent为父窗口，默认值为nullptr
    Widget(QWidget *parent = nullptr);
    // 析构函数，释放资源
    ~Widget();

protected:
    void wheelEvent(QWheelEvent *event) override;        // 重写缩放事件
    void mousePressEvent(QMouseEvent *event) override;   // 鼠标按下事件
    void mouseMoveEvent(QMouseEvent *event) override;    // 鼠标移动事件
    void mouseReleaseEvent(QMouseEvent *event) override; // 鼠标释放事件
private slots:
    // 按钮点击槽函数，用于绘制五角星
    void on_btn_drawStar_clicked();
    // 按钮点击槽函数，用于绘制矩形
    void on_btn_drawRect_clicked();
    // 按钮点击槽函数，用于绘制椭圆
    void on_btn_drawEllipse_clicked();
    // 按钮点击槽函数，用于清除绘制内容
    void on_btn_clearDrawing_clicked();
    // DDA 或 Bresenham，此处使用数值微分法DDA实现：圆外接五角星，五角星由直线段构成，适合用直线扫描算法绘制。
    void drawLineDDA(QGraphicsScene *scene, int x1, int y1, int x2, int y2);
    // DDA 或 Bresenham + 中点圆算法，此处使用中点画线法实现：圆内接正方形，正方形由直线构成，圆的绘制适合用中点圆算法。
    void drawMidpointCircle(QGraphicsScene *scene, int centerX, int centerY, int radius);
    // 中点椭圆算法实现绘制圆外切椭圆，椭圆外切圆的绘制适合使用中点圆算法和中点椭圆算法。
    void drawMidpointEllipse(QGraphicsScene *scene, int centerX, int centerY, int a, int b);

private:
    Ui::Widget *ui;        // UI界面的指针，用于访问界面元素
    QGraphicsScene *scene; // 图形场景，用于绘制图形
    int x, y, radius;      // 圆心坐标和半径，用于绘制圆
    bool isDragging;       // 标记是否正在拖动视图
    QPoint lastMousePos;   // 上次鼠标位置
};

#endif // WIDGET_H

widget.cpp

#include "widget.h"
#include "ui_widget.h"

// 构造函数，初始化UI和场景
Widget::Widget(QWidget *parent)
    : QWidget(parent)                 // 调用父类QWidget的构造函数
    , ui(new Ui::Widget)              // 创建UI对象
    , scene(new QGraphicsScene(this)) // 创建QGraphicsScene对象，指定parent为当前对象
    , isDragging(false)               // 初始化拖动标志
{
    ui->setupUi(this);                         // 设置UI界面
    ui->graphicsView_drawing->setScene(scene); // 将图形视图设置为当前场景
    ui->graphicsView_drawing->setRenderHint(QPainter::Antialiasing);      // 启用抗锯齿
    ui->graphicsView_drawing->setDragMode(QGraphicsView::ScrollHandDrag); // 设置拖动模式
    x = ui->graphicsView_drawing->width() / 2;  // 圆心的x坐标为图形视图宽度的中心
    y = ui->graphicsView_drawing->height() / 2; // 圆心的y坐标为图形视图高度的中心
    radius = ui->graphicsView_drawing->width() / 3; // 半径为图形视图宽度的三分之一
}

// 析构函数，释放UI对象
Widget::~Widget()
{
    delete ui; // 释放UI内存
}

void Widget::wheelEvent(QWheelEvent *event)
{
    int delta = event->angleDelta().y();
    qreal scaleFactor = (delta > 0) ? 1.2 : 0.8;

    // 获取当前缩放因子
    qreal currentScale = ui->graphicsView_drawing->transform().m11();

    // 设置缩放的最大最小值
    if ((scaleFactor > 1 && currentScale < 5) || (scaleFactor < 1 && currentScale > 0.1)) {
        ui->graphicsView_drawing->scale(scaleFactor, scaleFactor);
    }

    // 保持视图居中
    ui->graphicsView_drawing->centerOn(scene->sceneRect().center());
}

void Widget::mousePressEvent(QMouseEvent *event)
{ // 鼠标左键按下时，记录位置并开始拖动
    if (event->button() == Qt::LeftButton) {
        isDragging = true;
        lastMousePos = event->pos();     // 记录当前鼠标位置
        setCursor(Qt::ClosedHandCursor); // 改变鼠标为拖动状态
    }
}

void Widget::mouseMoveEvent(QMouseEvent *event)
{
    if (isDragging) {
        // 计算鼠标移动的距离
        QPoint delta = event->pos() - lastMousePos;
        ui->graphicsView_drawing->translate(delta.x(), delta.y()); // 移动视图
        lastMousePos = event->pos();                               // 更新鼠标位置
    }
}

void Widget::mouseReleaseEvent(QMouseEvent *event)
{ // 鼠标左键释放时，停止拖动
    if (event->button() == Qt::LeftButton) {
        isDragging = false;
        setCursor(Qt::ArrowCursor); // 恢复鼠标为箭头状态
    }
}

// 绘制圆外接五角星图像
void Widget::on_btn_drawStar_clicked()
{
    on_btn_clearDrawing_clicked();             // 清空当前绘制的图像
    const int points = 5;                      // 五角星有五个顶点
    double angleIncrement = 2 * M_PI / points; // 计算每个顶点的角度间隔
    double startAngle = -M_PI_2;               // 从顶部开始绘制五角星

    // 计算五角星顶点的坐标
    int starCoords[5][2];
    for (int i = 0; i < points; ++i) {
        double angle = startAngle + i * angleIncrement; // 计算当前顶点的角度
        starCoords[i][0] = x + radius * cos(angle);     // x 坐标
        starCoords[i][1] = y + radius * sin(angle);     // y 坐标
    }

    // 按五角星的顶点连接顺序绘制线段
    for (int i = 0; i < points; ++i) {
        int nextIndex = (i + 2) % points; // 跳过一个顶点连接（非相邻顶点）
        drawLineDDA(scene,
                    starCoords[i][0],
                    starCoords[i][1],
                    starCoords[nextIndex][0],
                    starCoords[nextIndex][1]); // 绘制线段
    }

    // 绘制外接圆
    scene->addEllipse(x - radius, y - radius, 2 * radius, 2 * radius, QPen(Qt::blue, 2));
}

// 绘制圆内接正方形图像
void Widget::on_btn_drawRect_clicked()
{
    on_btn_clearDrawing_clicked();   // 清空当前绘制的图像
    int side = radius * sqrt(2) / 2; // 正方形的边长，使用勾股定理求得
    drawLineDDA(scene, x - side, y - side, x + side, y - side);                           // 上边
    drawLineDDA(scene, x + side, y - side, x + side, y + side);                           // 右边
    drawLineDDA(scene, x + side, y + side, x - side, y + side);                           // 下边
    drawLineDDA(scene, x - side, y + side, x - side, y - side);                           // 左边
    scene->addEllipse(x - radius, y - radius, 2 * radius, 2 * radius, QPen(Qt::blue, 2)); // 绘制外接圆
}

// 绘制圆外切椭圆图像
void Widget::on_btn_drawEllipse_clicked()
{
    on_btn_clearDrawing_clicked(); // 清空当前绘制的图像
    double aspectRatio = 1.5;     // 椭圆的长短轴比例（1.5表示长轴是短轴的1.5倍）
    int a = radius * aspectRatio; // 长轴
    int b = radius;               // 短轴
    drawMidpointEllipse(scene, x, y, a, b); // 绘制椭圆
    scene->addEllipse(x - radius, y - radius, 2 * radius, 2 * radius, QPen(Qt::blue, 2)); // 绘制外接圆
}

// 清空当前绘制的图像
void Widget::on_btn_clearDrawing_clicked()
{
    scene->clear(); // 清除图形场景中的所有项
}

// 使用DDA算法绘制直线
void Widget::drawLineDDA(QGraphicsScene *scene, int x1, int y1, int x2, int y2)
{
    int dx = x2 - x1;                       // 计算x方向的差
    int dy = y2 - y1;                       // 计算y方向的差
    int steps = std::max(abs(dx), abs(dy)); // 选择更大的方向进行扫描
    float xInc = dx / float(steps);         // 计算每步x的增量
    float yInc = dy / float(steps);         // 计算每步y的增量

    float x = x1, y = y1; // 设置起始点
    for (int i = 0; i <= steps; i++) {
        scene->addRect(x, y, 1, 1, QPen(Qt::black)); // 绘制一个像素点
        x += xInc;                                   // 更新x坐标
        y += yInc;                                   // 更新y坐标
    }
}

// 使用中点圆算法绘制圆
void Widget::drawMidpointCircle(QGraphicsScene *scene, int centerX, int centerY, int radius)
{
    int x = 0, y = radius; // 初始化圆的初始坐标
    int d = 1 - radius;    // 初始判别值

    // 绘制圆的对称点
    auto plotCirclePoints = [&](int cx, int cy, int x, int y) {
        scene->addRect(cx + x, cy + y, 1, 1, QPen(Qt::blue));
        scene->addRect(cx - x, cy + y, 1, 1, QPen(Qt::blue));
        scene->addRect(cx + x, cy - y, 1, 1, QPen(Qt::blue));
        scene->addRect(cx - x, cy - y, 1, 1, QPen(Qt::blue));
        scene->addRect(cx + y, cy + x, 1, 1, QPen(Qt::blue));
        scene->addRect(cx - y, cy + x, 1, 1, QPen(Qt::blue));
        scene->addRect(cx + y, cy - x, 1, 1, QPen(Qt::blue));
        scene->addRect(cx - y, cy - x, 1, 1, QPen(Qt::blue));
    };

    // 使用中点圆算法绘制圆
    while (x <= y) {
        plotCirclePoints(centerX, centerY, x, y); // 绘制八个对称点
        if (d < 0) {
            d += 2 * x + 3; // 如果判别值小于0，更新x，保持y不变
        } else {
            d += 2 * (x - y) + 5; // 如果判别值大于等于0，更新y，同时减少y
            y--;
        }
        x++; // 更新x坐标
    }
}

// 使用中点椭圆算法绘制椭圆
void Widget::drawMidpointEllipse(QGraphicsScene *scene, int centerX, int centerY, int a, int b)
{
    int x = 0, y = b;
    double a2 = a * a, b2 = b * b;
    double d = b2 - a2 * b + 0.25 * a2; // 初始判别值

    // 绘制椭圆的对称点
    auto plotEllipsePoints = [&](int cx, int cy, int x, int y) {
        scene->addRect(cx + x, cy + y, 1, 1, QPen(Qt::red));
        scene->addRect(cx - x, cy + y, 1, 1, QPen(Qt::red));
        scene->addRect(cx + x, cy - y, 1, 1, QPen(Qt::red));
        scene->addRect(cx - x, cy - y, 1, 1, QPen(Qt::red));
    };

    // 第一阶段：沿y轴递减
    while (b2 * x <= a2 * y) {
        plotEllipsePoints(centerX, centerY, x, y); // 绘制四个对称点
        if (d < 0) {
            d += b2 * (2 * x + 3); // 如果判别值小于0，更新x
        } else {
            d += b2 * (2 * x + 3) + a2 * (-2 * y + 2); // 如果判别值大于等于0，更新y并减少y
            y--;
        }
        x++; // 更新x坐标
    }

    // 第二阶段：沿x轴递增
    d = b2 * (x + 0.5) * (x + 0.5) + a2 * (y - 1) * (y - 1) - a2 * b2;
    while (y >= 0) {
        plotEllipsePoints(centerX, centerY, x, y); // 绘制四个对称点
        if (d > 0) {
            d += a2 * (-2 * y + 3); // 如果判别值大于0，更新y
        } else {
            d += b2 * (2 * x + 2) + a2 * (-2 * y + 3); // 如果判别值小于等于0，更新x
            x++;
        }
        y--; // 更新y坐标
    }
}

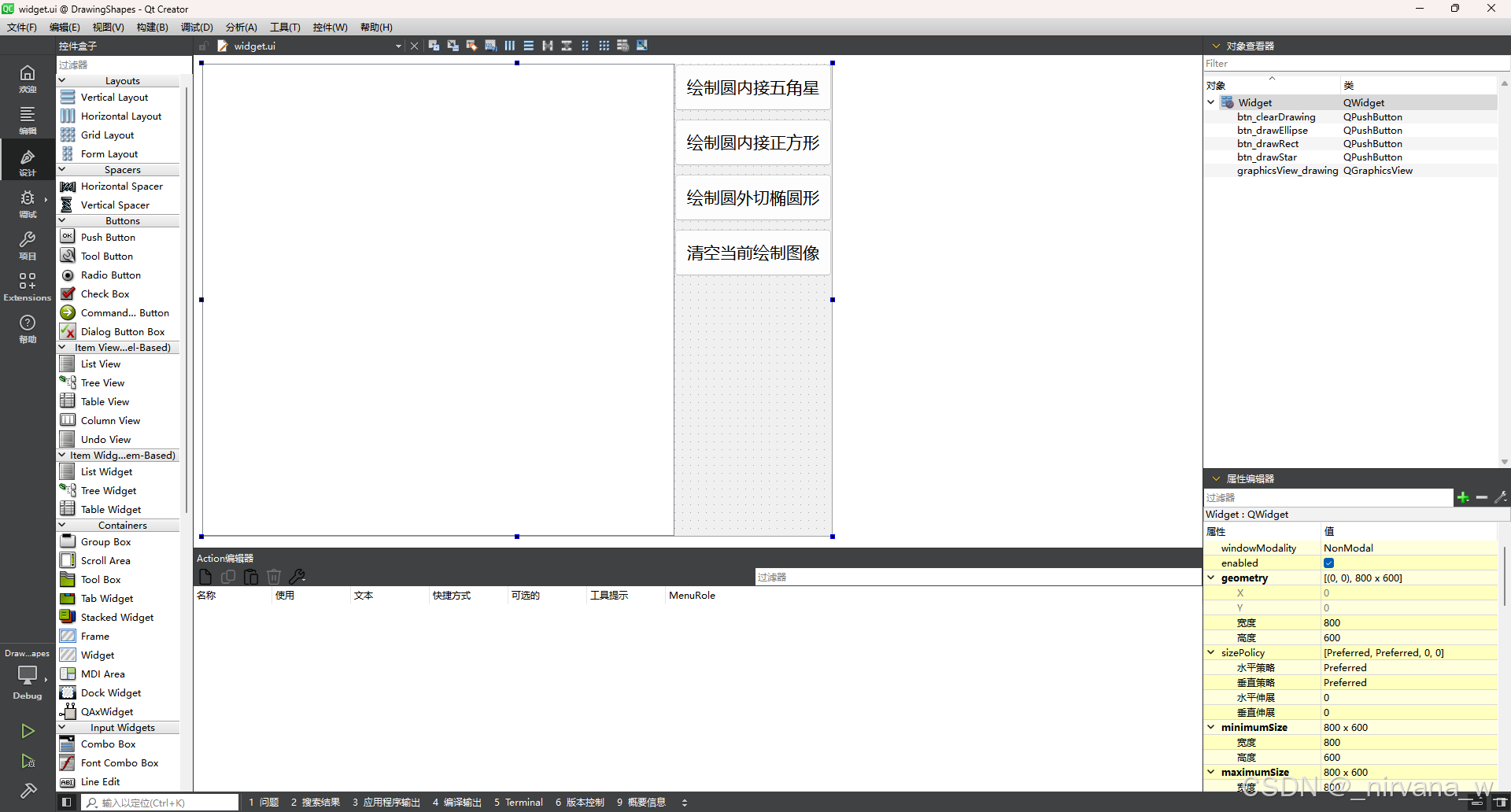
附界面设计文件截图

在这里插入图片描述

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

_nirvana_w_

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值