贪心算法三大问题（区间问题，Dijkstra算法，装载问题）python

1.区间问题

问题描述：

实现活动安排问题的贪心算法

已知：有一个场地要求每个活动使用同一资源，有多重活动并给出了活动的开始时间和结束时间si && fi

求解：求出在一定的时间内出场的活动最多？

问题分析：

这是一个区间问题，我们要求的是在不重叠的前提下尽可能多的在使用同一资源的情况下举办较多的活动，那么我们可以先思考，贪心算法贪的是什么？贪的东西就是算法的核心，那么在本题我们知道，贪的是“哪个活动结束得早，预留的时间就会更多”因此我们可以按照每个活动结束的时间进行一次排序，保证不重叠就是核心。看伪代码：

1.首先，我们将活动按照结束时间的早晚进行排序。

2.初始化一个变量 current_time 为 0，表示当前时间。
遍历所有的活动，对于每个活动：
如果该活动的开始时间晚于 current_time，说明这个活动与当前已选择的活动不冲突，那么就可以在 current_time 安排该活动。

3.将 current_time 更新为该活动的结束时间。

4.最后，我们计算并输出最终的活动数量。这是通过用总的活动数量减去最后选择的活动的结束时间加上开始时间来得到的。因为我们选择的活动都是不冲突的，所以最后选择的活动的结束时间加上开始时间应该等于当前时间 current_time。

撸代码：

# 贪心算法--区间问题概括（会场安排问题）
def activity_selection(s, f):
    # 将活动按照结束时间的早晚进行排序
    # 先做一个排序看贪心算法贪的是什么？是活动的结束时间
    # zip用作将列表中的元素对应起来返回一个列表且每个元素都是元组zip是一个可迭代对象元素用在后面的lambda表达式
    events = sorted(zip(s, f), key=lambda x: x[1])
    # events返回的是一个迭代器就是zip返回的元素作为元素的一个列表
    n = len(events)
    # 初始化一个变量 current_time 为 0，表示当前时间
    current_time = 0
    # 遍历所有的活动，对于每个活动
    count = 0
    for i in range(n):
        # 如果该活动的开始时间晚于 current_time，那么就可以在 current_time 安排该活动，将 current_time 更新为该活动的结束时间
        if events[i][0] >= current_time:
            current_time = events[i][1]
            count += 1
    # 输出最终的活动数量
    return count


print(activity_selection([4, 6, 4, 1], [5, 7, 6, 4]))

2.Dijkstra算法

我们将会以一个实例讲解！

问题描述：

实现单源最短路径的贪心算法

单源最短路径问题是在图中找到从一个源顶点到所有其他顶点的最短路径。这里我Dijkstra算法，这是一种解决单源最短路径问题的贪心算法

Dijkstra算法的基本思想是：每次从未被访问过的顶点中选择一个距离最小的顶点进行访问。在访问该顶点后，更新其他未访问的顶点到源顶点的距离。算法不断进行直到所有的顶点都被访问

问题分析：

首先呀，我们要有一个有向图，这里我准备了一个：

graph = {
    'A': {'B': 1, 'C': 3},
    'B': {'A': 1, 'C': 2, 'D': 4},
    'C': {'A': 3, 'B': 2},
    'D': {'B': 4},
    'E': {}
}

其实画出图之后：

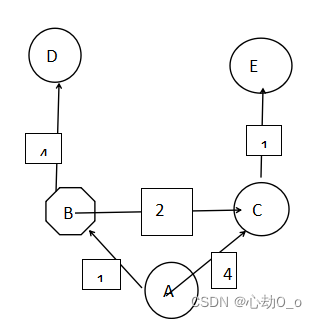
有了图之后开始分析问题：还是要找这个贪心算法的核心就是贪的是什么？要求路径最小值，那是不是我们每次走的路（能走的路）取值都是最小的，就是用局部最优解来推出全局最优解。知道这就差不多了·，我们开始分析问题：

伪代码：

输入：带权有向图G=<V,E,W>,源点s属于V

输出：数组L，对所有j属于V-S，L[j]表示s到j的最短路径上j前一个结点的符号

S←{s}

dist{s}←0

for i∈V-S do

   dist[i]←w(s,i)

while V-S≠∅ do

   从V-S中取出具有相对S的最短路径的结点j，k是该路径上连接j的结点

   S←S∪{j}

   L[j]=k

   for i∈V-S do

       if dist[j]+w(j,i)<dist[i]

       then dist[i]=dist[j]+w(j,i)     //修改结点i相对S的最短路径长度

通过分析之后，我们知道每次循环都走一步，然后可能会修改之前走的路，但是每次都保证所取得值都是该路径的最小值。

撸代码：

# 贪心算法--Dijkstra算法（解决单源最短路径问题的贪心算法）
import heapq  # 导入Python的优先队列模块。


def dijkstra(graph, start):  # 定义Dijkstra算法的函数，它接受一个图和一个源顶点作为输入
    # 初始化距离字典，设置所有顶点到源顶点的距离为无穷大记住格式
    dict = {key: float('infinity') for key in graph}  # 遍历图的所有节点graph是一个图
    # 设置源顶点到自己的距离为0
    dict[start] = 0

    # 初始化优先队列，首先将源顶点加入队列
    num_1 = [(0, start)]  # 初始化一个优先队列，开始时队列中只有一个元组，即源顶点及其从源顶点到该顶点的距离（0）前面一个数是距离后面一个是源点

    while num_1:
        # 从优先队列中取出距离最小的顶点
        # 优先队列是一种数据结构，它可以根据元素的优先级进行插入和删除操作
        # 接着取优先队列中的下一个元素即取过的元素不在取出
        current_distance, current_vertex = heapq.heappop(num_1)  # 分解这个元素，得到最小值（赋值给current_distance）和健（赋值给current_vertex）
        # 如果已经计算过的顶点到源顶点的距离小于当前距离，就忽略此次取出操作
        if current_distance > dict[current_vertex]:  # current_distance是当前从优先队列中取出的顶点到源顶点的距离，而d[current_vertex]是已经计算过的顶点到源顶点的距离
            continue
        # 遍历邻居，更新它们到源顶点的距离
        # 进行的遍历是针对嵌套字典中的内层
        # 对于嵌套字典来说，items() 方法会返回嵌套字典的所有子项。
        # 因此，在这段代码中，graph[vertex].items() 返回了 graph[vertex] 字典中的所有键-值对，即当前节点的所有邻居及其对应的距离
        for neighbor, distance2 in graph[current_vertex].items():  # 注意是在哪遍历的,遍历的是图（嵌套字典形式）
            # items() 方法。这个方法返回一个包含字典所有项的列表，然后通过遍历这个列表，我们可以访问每个项即items方法返回的列表还会进行一次自动遍历
            distance = current_distance + distance2
            # 如果新的距离小于已知的距离，则更新距离并将邻居加入优先队列
            if distance < dict[neighbor]:  # 在字典中初始化了每个健key的value为无穷大，所以第一次出现的健就会采用以后再更新
                dict[neighbor] = distance
                # heapq.heappush(heap, item)：将元素item插入堆(即优先队列)heap中。
                heapq.heappush(num_1, (distance, neighbor))

    return dict

# 创建一个图以嵌套字典的形式表示为图，在纸上画出图可以看出节点的连接方式。


graph = {
    'A': {'B': 1, 'C': 3},
    'B': {'A': 1, 'C': 2, 'D': 4},
    'C': {'A': 3, 'B': 2},
    'D': {'B': 4},
    'E': {}
}

# 调用 Dijkstra 函数并输出结果  初始化一个顶点‘A’
result = dijkstra(graph, 'A')
print(result)  # 输出: {'A': 0, 'B': 1, 'C': 3, 'D': 5, 'E': inf}

3.装载问题

问题描述：

有一批集装箱要尽可能多的装载在额定重量c货轮上，再不受空间限制的条件下集装箱重量i 重量wi

尽可能多的装载。

问题分析：

贪心策略贪的是什么？我们还是先找核心，”贪的是重量轻的先上船找重量轻的集装箱”。

直接上代码：

# 贪心算法--装载问题（轮船装载重量最高）
def greedy_loading(c, w):
    # 按照单位重量对物品进行排序
    sorted_w = sorted(w)
    total_weight = 0
    loaded_weight = 0
    count = 1
    for i in range(len(sorted_w)):
        # 如果当前物品可以全部装载，那么就全部装载
        if total_weight + sorted_w[i] <= c:
            total_weight += sorted_w[i]
            loaded_weight += sorted_w[i]
            print(f"装载物品 {sorted_w[i]}，已装载重量：{loaded_weight}")
            count += 1
        # 如果当前物品不能全部装载，那么就装载一部分
        elif i > 0 and sorted_w[i] < sorted_w[i - 1]:
            ratio = c - total_weight
            if ratio < sorted_w[i - 1] - sorted_w[i]:
                total_weight += sorted_w[i - 1] - ratio
                loaded_weight += sorted_w[i - 1] - ratio
                print(f"装载物品 {sorted_w[i - 1]}（部分），已装载重量：{loaded_weight}")
            else:
                total_weight += sorted_w[i]
                loaded_weight += sorted_w[i]
                print(f"装载物品 {sorted_w[i]}，已装载重量2：{loaded_weight}")
        else:
            break
    return loaded_weight, count-1


c = 70
w = [20, 10, 26, 15, 51, 16]
print(greedy_loading(c, w))

上面的是贪心算法，之前呢我理解错了题，把他看成了背包问题不过可以当做复习动态规划了：

# 动态规划方法求解（常规解法）
def loading(c, w):
    n = len(w) - 1
    dp = [[0 for _ in range(c + 1)] for _ in range(n + 1)]
    for i in range(1, n + 1):
        for j in range(1, c + 1):
            if j >= w[i]:
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + w[i])
            else:
                dp[i][j] = dp[i - 1][j]
    return dp[n][c]


c = 70
w = [0, 20, 10, 26, 15]
print(loading(c, w))

我一看动态规划简单了不少但是看错题了！

总结一下：

贪心算法其实就是要找出贪的是什么？这就是核心。我觉得每个贪心算法的题呢不像动态规划那样有模板可以套用，如果遇到特别难的题也只能寄寄了！