CF round 900题解 A~D

A. How Much Does Daytona Cost?

A. How Much Does Daytona Cost?

题目大意

给定一个数组，给定一个整数k，求数组中是否有一子段中的k是最常见元素（子串中k元素的数目唯一最多）。

思路

案例可以得知，子段长度为一且值为k也是符合要求的，所以只需要找数组中是否有k这个元素就好了。

AC代码

#include<bits/stdc++.h>
using namespace std;
int main(){
    int t;
    cin>>t;
    while(t--){
        int f=0;
        int n,k; cin>>n>>k;
        for(int i=1;i<=n;i++){
            int x; cin>>x;
            if(x==k) f=1;
        }
        if(f==1) cout<<"YES"<<endl;
        else cout<<"NO"<<endl;
    }
}

B. Aleksa and Stack

B. Aleksa and Stack

题目大意

给定一个整数n，构造一个大小为 n的正整数严格递增数组，数组结构如下：

思路

奇数+奇数=偶数，奇数*3=奇数，奇数不能整除偶数，所以数组的构造方法就找到了。

AC代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int M=2e5+5;
ll a[M];
int main(){
    int t ; cin>>t;
    while(t--){
        int n; cin>>n;
        a[1]=1; a[2]=3; a[3]=5;
        for(int i=4;i<=n;i++){
            a[i]=a[i-1]+2;
        }
        for(int i=1;i<=n;i++){
             cout<<a[i]<<" ";
        }
        cout<<endl;
    }
}

C. Vasilije in Cacak

C. Vasilije in Cacak

题目大意

给Vasilije三个正整数:n， k 和 x，他必须确定他是否可以在 1和 n 之间选择 k个不同的整数，使它们的和等于 x。

思路

求出1~k和 n-k+1 ~n 的前缀和，判断x是否在这两个前缀和之间，如果在就存在，否则就不存在。

证明

求k个数的和，如果x的和为1+2+3+……+ k-1 + k+1；就把k去掉换成k+1就行了，最差的情况就是1~k完全换成了最后k个数。

AC代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int M=2e5+5;
ll sum[M];
int main(){
    for(int i=1;i<=M;i++) sum[i]=sum[i-1]+i;
    int t; cin>>t;
    while(t--){
        ll n,k,x; cin>>n>>k>>x;
        
        if(x>=sum[k]&&x<=sum[n]-sum[n-k]){
            cout<<"YES"<<endl;
        }
        else cout<<"NO"<<endl;
    }
}

D. Reverse Madness

题目大意

一个给定字符串，经过数次区间翻转后，输出修改后的字符串

思路

首先这个题不能暴力求解，即使我们通过二分找到了给定的x所在的区间，然后每次都要翻转，时间复杂度也依旧在O（n*q）。这个时间复杂度1s钟完不成，但是q是固定的，所以只能在翻转字符串的操作上面优化。

题目中给出了两个关系


可以根据这两个关系得出

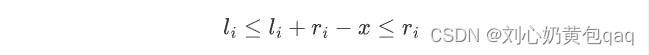
也就是说字符串每次翻转的区间都在l_i ~ r_i的区间内

得出这一点后，在一个区间内翻转，若一个区间翻转两次的话，相当于没有变，他的影响就可以被忽视，所以就可以用一个差分数组，记录每个区间的翻转次数，奇数次的区间就需要翻转，并且只用遍历区间的一半就行了，因为翻转是对称的。

l+r-x就代表了x相对于区间中点对称的位置。

这样时间复杂度就被缩小为了O（k*n/2）

AC代码

#include<iostream>
#include<algorithm>
using namespace std;
const int M = 2e5 + 5;
int l[M];
int r[M];
int cha[M];
int main() {
	int t; cin >> t;
	while (t--) {
		int n, k; cin >> n >> k;
		string s; cin >> s;
		s = " " + s;
		for (int i = 1; i <= n; i++) cha[i] = 0;
		for (int i = 1; i <= k; i++) {
			cin >> l[i];
		}
		for (int i = 1; i <= k; i++) {
			cin >> r[i];
		}
		int q; cin >> q;
		for (int i = 1; i <= q; i++) {
			int x; cin >> x;
			int pos = lower_bound(r + 1, r + 1 + k, x) -r;
		//	cout <<"pos:  " << pos << " ";
			int L, R;
			L = l[pos]; R = r[pos];
			int a = min(x, L + R - x); int b = max(x, L + R - x);
			cha[a]++; cha[b + 1]--;
		//	cout << "a: " << a << " " << "b: " << b << " ";
		//	reverse(s.begin() + a-1, s.begin() + b);
		}
		for (int i = 1; i <= n; i++) cha[i] += cha[i - 1];
		for (int i = 1; i <= k; i++) {
			for (int j = l[i]; j <= (l[i] + r[i]) / 2; j++) {
				if (cha[j]&1)
					swap(s[j], s[l[i] + r[i] - j]);
			}
		}
		s.erase(0, 1);
		cout << s<< endl;
	}

}