计算机组成原理

二：数据的表达和运算

数据表示

进制	英文简写
二进制	B
八进制	O
十进制	D
十六进制	H

   每一位十六进制数与四位二进制数对应，每一位八进制数与三位二进制数对应。

注意：并不是所有十进制小数都可以准确的转换为二进制小数。 

真值： 带“+”“-”符号的数。（机器数的实际值）

​​机器数​​：计算机中用于表示数值的二进制形式，其特点包括固定位数、符号处理和特定编码规则。

        常见编码方式​：原码，反码，补码，移码.

• 原码：总共有n+1位。最高位是符号位，0表示正号，1表示负号。其余n 为位表示数值的绝对值。

• 反码：正数的反码与原码相同，负数的反码则是原码数据位按位求反。

• 补码：正数的补码与其原码和反码相同，负数的补码则是等于其反码的末位加1。）（补码可以简化计算机运算部件的设计）

• 移码：在补码的基础上取反符号位。（只能表示整数），用来比较大小

---

n+1位机器数：1位符号位+ n位数值部分。

定点小数：

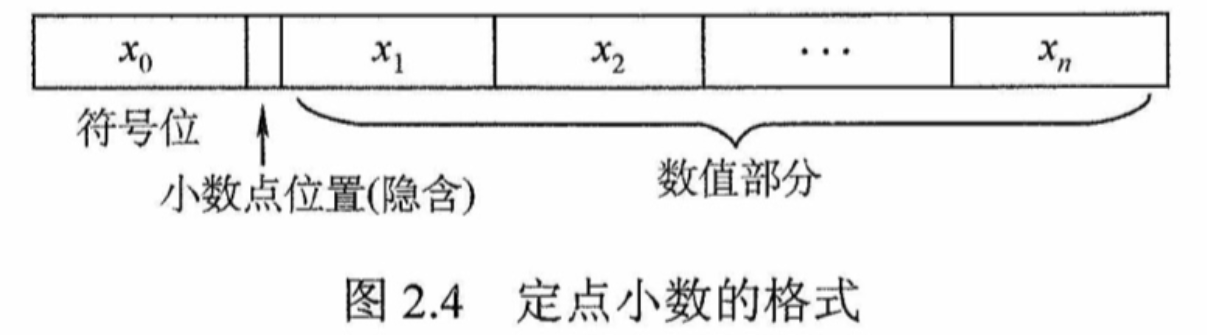
        表示范围 -(1- 2^-n) ～ 1- 2^-n（总共n+1位）

    

---

定点整数：

表示范围 ：-(2^n -1 ) ～ 2^n -1（总共n+1位）

---

（补充）补码原理：

用加法代替减法，用补码计算的时候，符号位也进行运算

首先引入：mod （模）的概念

mod m ，会将所有的整数分为【0，m-1】m个数

mod 后想等的数（是等价的）可以相互替换，

所以用补码来代替该数进行运算不改变结果。

eg：

（10+9） mod 12 =7 ，（10+（-3）） mod 12 =7，

•          所以：用9 和（-3）去进行运算得到的结果都是一样的。（因为在计算机内计算后的值也是需要mod 的，因为高位要舍弃）

    所以对负数的运算可以转换成正数（该负数的补码）

注：因为字长有限：所以高位肯定要舍去，实现的方式就是mod。

计算机 eg机器字长 n，可以看成对所有数据都是mod 2 ^n (将所有数映射到【0，2^n -1】内)

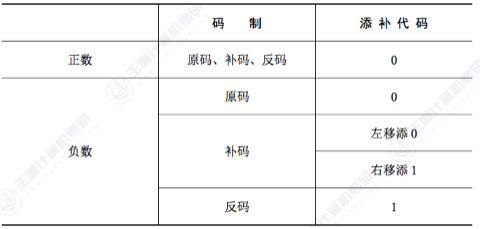
原反补移表示范围

因为补码和移码的+0和-0 表示一样，所以负值的范围要大1. 如下图所示：

从图中也可以看出，移码从小到大，也是其对应真值从下到大。移码大小和对应真值正比，所以比较大小都是用移码比较。

---

移位

算数移位

（算数移位：看作有符号数）

   左移相当于×2；右移相当于÷2，（2是基数）

由于位数有限，因此有时候无法用算数移位精确地等效乘除法       

        原码算术移位：左移丢1，运算出错；右移丢1，影响精度。

逻辑移位

逻辑移位：将操作数看作无符号进行操作，都是补0

溢出

逻辑左移 还是 算术左移，在某些情况下都可能改变符号位。，符号位不参与移位，但符号位上的数字是参与移位的

补码左移动时候：符号参与移位，如果符号位，如果移动后符号位的地方的数变了，说明溢出了。

移除的数和符号位的数不同时：就发生了溢出