离散数学期末笔记

命题逻辑

命题及其表示法

推理的前提和结论都是表达判断的陈述句。

命题：有确定真值的陈述句

分类：

原子命题：不能分解为更简单的陈述句。

复合命题：若干个原子命题、连词、标点符号

命题连接词

命题公式和翻译

命题常元:真值唯一，确定，例如:T、F

命题变元: P、Q、R
命题联结词:^

合式公式：合法的命题公式，需要规定优先级

运算规定：

真值表与等价艺术

真值表：对于分量指派真值的各种可能组合

基本等价公式

等价置换：设X为合式公式A的子公式，若X等价 Y，如果用Y置换A
中的X，得到公式B,则A等价B。

重言式与蕴含式

重言式：永为T 矛盾式F

蕴含式

主析取范式

最小联结词 否 析取 合取（小项）

没有两个小项是等价的，且每个小项都只对应P和Q的
组真值指派，使得该小项的真值为T。

直接证法

P规则(前提引入规则):在推导过程中，前提可视需要引入使用。前提
可以用在证明过程中的任何步骤中。
T规则(结论引入规则):在推导中，如果有一个或多个公式、重言蕴含
着公式S,则公式S可以引入推导之中。

条件论证

如果要证明的结论是R→S的形式，则可
以把结论中R→S的前件R作为附加前提，与
给定的前提一起推出后件S即可。

谓词逻辑

约定用大写字母表示谓词。
用小写字母表示客体名称。
小写字母写在大写字母右侧的圆括号( )内。

注意: A(x)本身不是命题， x取具体的客体时为一个命题。

个体域

客体变元的论述范围称作个体域。
把各个个体域综合在一起作为论述范围的域称全总个体域。

变元

        

谓词公式的赋值

在谓词公式中,当客体变元由确定的客体所取代，命题变元
用确定的命题所取代时，就称作对谓词公式赋值。 

前束范式

一个公式，如果量词均在全式的开头，它们的作用域，
延伸到整个公式的末尾，该公式叫做前束范式。

求解办法：

第一步:否定深入。即利用量词转化公式，把否定联结词深入
到命题变元和谓词填式的前面。
第二步:改名。即利用换名规则、代入规则更换一些变元的名
称，以便消除混乱。
第三步:量词前移。即利用量词辖域的收缩与扩张把量词移到
前面。这样便可求出与公式等价的前束范式。

量词

消去

全称量词消去规则（US）规则

存在量词消去规则（ES）规则

集合与关系

集合的关系

相等：两个集合A和B相等当且仅当它们具有相同的元素。

包含

真包含：如果集合A的每一个元素都属于B ,但集合B中至少有一个元素
不属于A，则称A为B的真子集，记作AcB

幂集：

集合的运算

交运算
并运算
差运算

对称差运算

运算律：

序偶与笛卡尔积

序偶：两个具有固定次序的客体组成一个序偶。常表示两个客体之间的关系。

笛卡尔积：定义:设A和B是任意两个集合，由A中元素作第一元素,B 中元素作第二元素
构成序偶，所有这样序偶的集合称集合A和B的笛卡尔积或直积，记作: AxB

性质：

前域和值域

R的前域和值域一起称作的域，记作FLD R。

关系

定义

XxY称为X到Y的全域关系，记作U。
0称为空关系。

关系的表示方法

有向图法：

矩阵表示法：

关系的性质

自反与反自反性

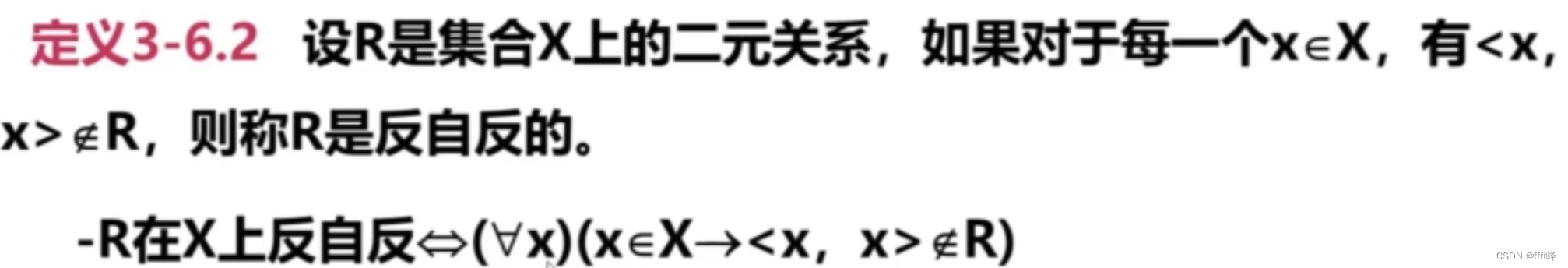
对称与反对称性

反对称性
传递性

复合关系和逆关系

        复合关系：

关系图表示：

矩阵表示：

逆关系：

关系的闭包运算

求解方法：

集合的划分与涵盖

覆盖：若把一个集合A分成若干个叫做分块的非空集合，使得A中每个元
素至少属于一个分块，那么这些分块的全体构成的集合叫做A的一个覆盖。

划分：如果A中每个元素属于且仅属于一个分块，那么这些分块的全体构成的集
合叫做A的一个划分(或分划)。

交叉划分：

加细：

任何两种划分的交叉划分，都是原来各划分的一
种加细。

等价关系和等价类

等价关系：设R为集合A上的二元关系,若R是自反的、对称的和传递的，则
称R为等价关系。
等价类

商集

相容关系

相容关系：设集合A上的关系R，若R是自反的、对称的，则称R为相容关系。

相容类

最大相容类：

最大完全多边形

完全覆盖：

序关系

偏序关系

盖住集合

链和反链

全序.

极大元极小元

若只有一个极大元则为最大元

上确界:所有上界中的最小者，最小上界:
下确界:所有下界中的最大者， 最大下界:

函数

函数的概念

函数的数量

概念的分类

满射：对于f: X→Y的映射中，如果ran f=Y,即Y的每一个元素是X中一个或多个元素的象点，则称这个映射为满射。

满射: | ran f|=|Y|。值域和y相等
入射：从X到Y的映射中，X中没有两个元素有相同的象，则称这个映射为入射(或一对一映射)
双射：如果f既是X到Y的入射，又是X到Y的满射，则称f为X到Y的双射函数。双射函数也称一一对应。

双射: | X|= |f(X)|= | Y|。

逆函数和复合函数

每一个函数的逆关系都存在，逆关系不一定是函数。

复合函数

两个函数的复合是一个函数。

性质

代数结构

上述例子中的运算结果都是在原来的集合中，我们称那
些具有这种特征的运算是封闭的，简称闭运算。相反的，
没有这种特征的运算就是不封闭的。

运算的表示

解析公式和运算表。

代数系统

运算的性质

设*是定义在集合A上的二元运算,
如果对任意x,y∈A，都有x*y∈A,则称运算*在A上是封闭的。

幂等律

特殊元素

幺元

零元

逆元

定理

总结

半群

子半群

是一个半群，如果S是一一个有限集，则必有等幂元

独异点

含有幺元的半群称为含幺半群或独异点。

群和子集

设<G, *>是一个代数系统，其中G是非空集合，*是G上一
个二元运算，如果

群的性质

群中无零元

满足消去律

置换

群<G, *>的运算表中的每一行或每一列都是G的元素的一个置换。

子群

平凡子群

一个最多 一个最少

设<G, *>是一个群，B是G的非空子集，
如果B 是一个有限集，那么，只要运算*在B.上封闭，<B, *>必定是<G, *>的子群。

阿贝尔群和循环群

如果群<G, *>中的运算*是可交换的，则称该群为阿贝尔群，或称交换群。

设<G, *>为群，若在G中存在一个元素a,使得G中的任意元素都由a的幂组成，则称该群为循环群，元素a称为循环群G的生成
元。

任何一个循环群必定是阿贝尔群。

图论

图的基本概念

图

无向图:每条边均为无向边的图称为无向图。
有向图:每条边均为有向边的图称为有向图。
混合图:有些边是无向边，有些边是有向边的图称为混合图。

度数

在图G=<V, E>中，与结点v关联的边数称为该结点的度数
点的度数，记为deg(v)。孤立结点的度数为0。环为2

握手定理

每个图中，结点度数总和等于边数的两倍。

在有向图中，射入一个节点的边数称为该节点的入度;由一个节点射出的边数称为该结点的出度。节点的出度和入度之和就是该节点的度数。

特殊的图

多重图:含有平行边的图称为多重图。
简单图:不含平行边和环的图称为简单图。
完全图:简单图G=<V, E>中，若每一对结点间均有边相连，则称
该图为完全图。有n个结点的无向完全图记为Kn。        

补图

子图

点相同时为生成子图

相对补图        

同构

必要条件

结点数目相同;
边数相等;
度数相同的结点数目相等。

路与回路

定义

v0和vn,分别叫做路的起点和终点,边的数目n称作路的长度

图的连通性

若图G只有一个连通分支，则称G是连通图。

删除结点:所谓在图中删除结点v,即是把v以及与v关联的边都删除。
删除边:所谓在图中删除某条边，即是把该边删除。

点连通度

边连通度

有向图的连通性

定理

图的矩阵表示

无向图

有向图

关联矩阵

有向图

欧拉图与汉密尔顿图

欧拉图

给定无孤立结点图G ,若存在一条路,经过图中每边一次且仅一次,该条路称为欧拉路;若存在一条回路,经过图中每边一次且仅一次，该回路称为欧拉回路。具有欧拉回路的图称为欧拉图。

无向图G具有一条欧拉路,当且仅当G是连通的,且有零个或两个奇数度结点。

无向图G具有一条欧拉回路,当且仅当G连通且所
有结点度数皆为偶数。

单项欧拉回路

哈密尔顿图

充分条件

图的闭包

平面图

设G=<V,E>是一个无向图,如果能够把G的所有结点和边画
在一个平面上,且使得任何两条边除了结点外没有其他的交点,就称G是
一个平面图，否则称G为非平面图。

面边界

一个有限平面图,面的次数之和等于其边数的两倍。

欧拉定理

同胚

树与生成树

树的定义

在给定结点的无向图中:树是边数最少的连通图，树是边数最多的无回路图。

生成树

生成树的存在性

权图

根树及其应用

根树

有向树

如果一个有向图在不考虑边的方向时是一棵树，那么该有向图称为有向树。

一棵有向树,如果恰有一个结点的入度为0,其余所有结点的入度都为1 ,则称为根树(rooted tree)。入度为0的结点称为T的树根。出度为0的结点称为树叶，出度不为0的结点称为分支点或内点。

树高

习惯把有向树的根画在最上方，边的箭头全指向下，则可以省略全部箭头，
对根到一个结点的有向通路的长度称为该点的层数。所有结点的最大层数称为树高。

相关定义

在根树中，若每个结点的出度小于或等于m， 则称这棵树为m叉树
如果每个结点的出度恰好等于0或m，则称这棵树为完全m叉树。

二叉树(binary tree )的每个结点v至多有两棵子树， 分别称为v的左子树和右子树。

 性质 

设有完全m叉树，其树叶的数目为t,分支数为i,则(m-1)xi=t-1。

设n为节点数n= m*i+1

设t为叶子节点, n=t+i

通路长度

在根树中， 一个结点的通路长度，就是从树根到该结点的通路中的边数。分支点的通路长度称为内部通路长度，树叶的通路长度称为外部通路长度。

设有完全二叉树有n个分支点，且内部通路长度总和为I，外部通
路长度总和为E，则E=I+2n。

最优树

哈夫曼算法

哈夫曼编码

前缀码

给定一个序列的集合,若没有一个序列是另一个序列的前缀，该序列集合称为前缀码。

例如: {0,10,110, 1111}是(2元)前缀码。

任意一棵二叉树的树叶可对应一个前缀码。