目录
📚堆的概念与结构
📑堆的概念
堆(Heap)是计算机科学中一类特殊的数据结构,是最高效的优先级队列。堆通常是一个可以被看作一棵完全二叉树的数组对象。
堆就是一个完全二叉树+数组存储的
如果有一个关键码的集合K = {k0,k1, k2,…,kn-1},把它的所有元素按完全二叉树(二叉树具体概念参见——二叉树详解)的顺序存储方式存储在一个一维数组中,并满足:Ki <= K2i+1 且 Ki<= K2i+2 (Ki >= K2i+1 且 Ki >= K2i+2) i = 0,1,2…,则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
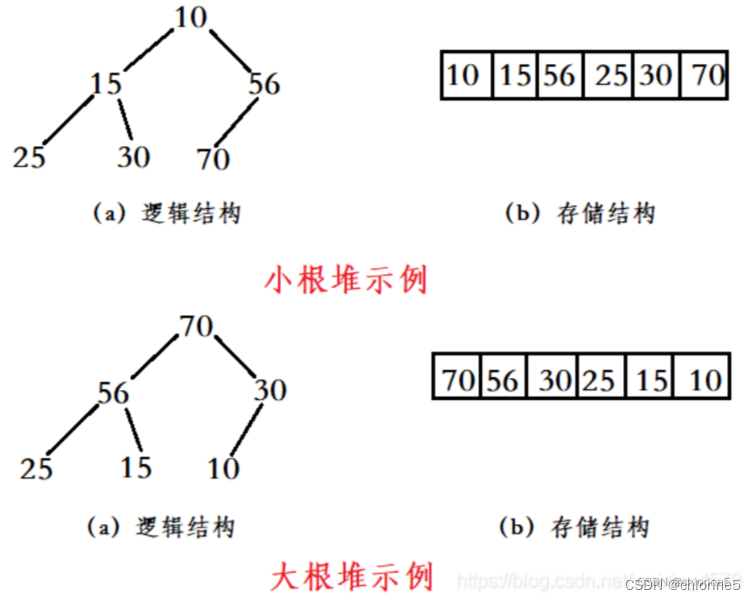
📑堆的性质
- 堆中某个节点的值总是不大于或不小于其父节点的值;
- 堆总是一棵完全二叉树,用数组来存储。
对于完全二叉树而言,已知父亲节点的下标为i,则
他的左孩子下标为2*i+1,右孩子下标为2*i+2
📑堆的意义
用来选数,因为比如大堆,父亲就是最大的,以后讲的堆排序就是用的这个特征,大堆特点:根(堆顶)就是最大值,小堆特点:根(堆顶)就是最小值。实际应用比如选出哪个地方好评最好的食品,就用到了堆。
📑例题
下列关键字序列为堆的是(A)
A、100,60,70,50,32,65
B、60,70,65,50,32,100
C、65,100,70,32,50,60
D、70,65,100,32,50,60
思路:因为堆的完全二叉树按照数组来存储,则从第一个往后每一层的节点数为1、2、4、6......
比如A:
📚堆的实现
堆的实现代码------堆的实现代码
🚩堆的向下调整算法
(此文章都已建小堆为例)大堆只要改变符号即可
向下调整算法前提:当前树左右子树都是小堆
前提:如果一棵树中左右子树都是小堆(或大堆),只有根节点不满足,那么就可使用向下调整算法。(这个方法很重要,讲的堆排序都要用到这个算法)数组建堆主要依赖的就是向下调整法
基础知识:对于完全二叉树而言,已知父亲节点的下标为i,则他的左孩子下标为2*i+1,右孩子下标为2*i+2
思路:找出左右孩子中小的那一个,然后与父亲节点交换,然后再找下一个父亲和孩子,再次找出左右孩子中小的那一个,不断比较并交换,直到最后的下标超出了数组的范围。
调整终止条件有两个:
- 当二叉树是满二叉树:child < n循环(调整)才会继续
- 当二叉树的最后某一节点只有左子树(不可能只有右子树,因为是完全二叉树),child+1<n循环(调整)才会继续,否则这种情况会越界
- 交换过程中满足孩子大于父亲了,说明此次无需交换了
🚩代码
//交换元素
void swap(HPDaTaType* p1, HPDaTaType* p2)
{
HPDaTaType x = *p1;
*p1 = *p2;
*p2 = x;
}
//向下调整法
void AdjustDown(HPDaTaType* a,int n, int parent)
{
//先假设,如果假设错误,就交换
int child = parent *2+1;//默认左孩子大
while (child < n)
{
选出左右孩子中大的那一个
if (child+1<n&&a[child + 1] > a[child])
//&&表达式,左表达式不满足,右表达式就不进行判断了
//如果右孩子比左孩子还小,就让child变成右孩子,即下标+1即可
{
++child;
}
if (a[child] > a[parent])
{
swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
🚩详细过程
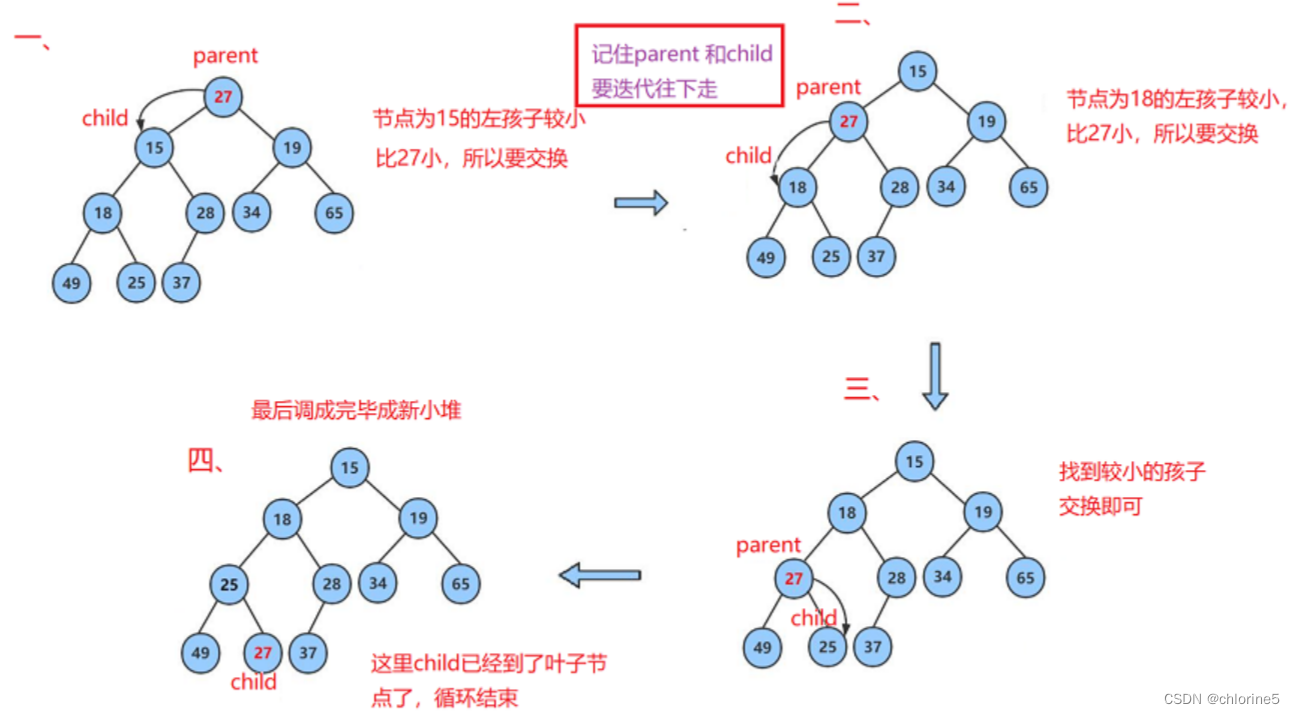
🚩向下调整法的时间复杂度
因为对于堆来说,按最糟糕的情况来算,那就是每一层就要交换一次节点,那么整个堆就要交换高度次,即log(N+1) (以2为底N+1的对数),故时间复杂度:O(logN)
【排降序】:建小堆
【排升序】:建大堆
🚩 实现向下建堆
这里我们可以利用刚刚写的堆的向下调整算法,我们知道,满足堆,必须左右子树都是大堆或者小堆,我们可以利用这个思想,从下往上倒着走,从第一个非叶子节点开始,通过数组下标的控制,把它当做根去向下调整,依次往上,直到把当前路径调整成符合条件的大堆或者小堆即可

//1.建堆 n为数组个数 n-1为最后一个元素下标 (n-1-1)/2找到第一个非叶子节点的父亲
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(hp->a, hp->size, i);
}
//排成升序
//2、找次小,排序
int end = n - 1;
while (end > 0)
{
swap(&a[end], &a[0]);
//再继续选次小的
//然后向下调整找到第二大的数
AdjustDown(a, end, 0);
end--;
//没有真的删除最后一个数据,只是说我下次再找小交换,最后一个数据
//不被看作堆里面的,不造成影响
}🚩向下建堆的时间复杂度(O(N))
已知向下建堆的时间复杂度为O(N),而在排序过程中,由于要每次选出剩余数中最小的数,并保存到每次最后的节点,并要再执行一次向下调整算法,总共需要进行N次,而向下调整算法的时间复杂度为O(logN),进行N次就是O(N*logN),即堆排序的时间复杂度

🌈堆的向上调整算法
当我们已经有一个堆,我们需要在堆的末尾插入数据,再对其进行调整,使其任然保持堆的结构,这里我们就需要用到堆的向上调整算法
堆的向上调整算法基本思想:(以建小堆为例)
①将要插入的数据与其父节点数据比较
②若子节点数据小于父节点数据,则交换
若子节点数据大于父节点数据,则不交换,不需要调整,已经满足堆的结构
🌈代码
void Swap(int* x, int* y)
{
int* tmp = *x;
*x = *y;
*y = tmp;
}
void AdjustUp(int * a, int child)
{
int parent = (child - 1) / 2;
while (child>0)
{
if (a[parent] > a[child])
{
Swap(&a[child],&a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
🌈详细过程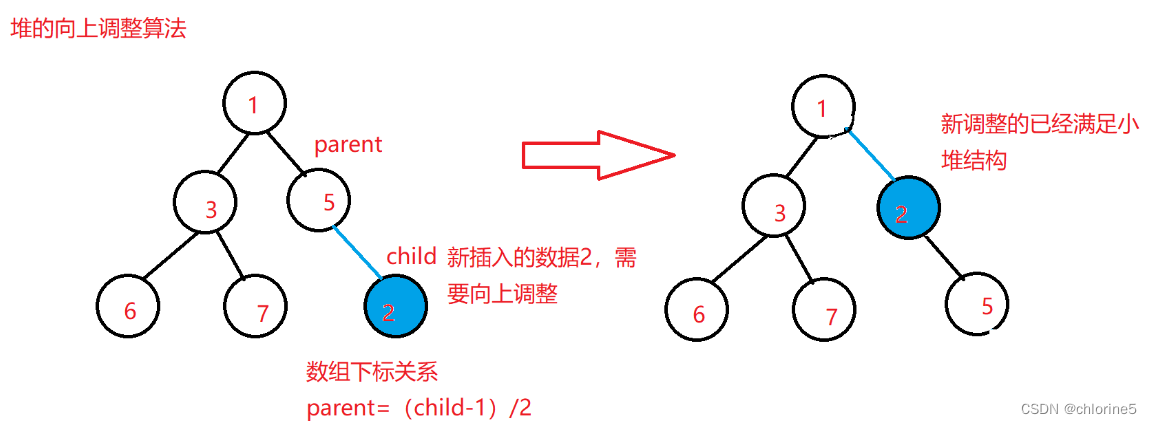
🌈向上调整法的时间复杂度
因为对于堆来说,按最糟糕的情况来算,那就是每一层就要交换一次节点,那么整个堆就要交换高度次,即log(N+1) (以2为底N+1的对数),故时间复杂度:O(logN)
【排降序】:建小堆
【排升序】:建大堆
🌈实现向上建堆
//建堆,向下调整法
for(int i=0;i<n;i++)
{
AdjustUP(a,i);
}
🌈 向上建堆的时间复杂度(N*logN)
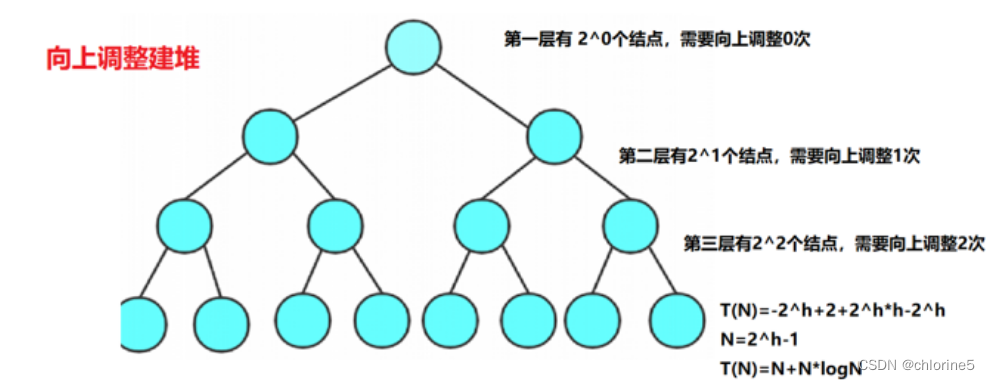
📚总结:

向上调整法复杂度=向下调整法时间复杂度=O(logN)
向下建堆的时间复杂度:O(N)
向上建堆的时间复杂度:O(N*logN)
堆排序的时间复杂度:O(N*logN)(向下建堆基础)

我们可以看上面对比
- 向下调整法建堆,第一层一个结点,向下调整h-1层,但是到最后一层的结点最多,但是只需要向下调整1层即可
- 向上调整法建堆,第一层一个结点,调整0层,但是到了最后一层结点最多,但是要调整h-1层,那么大大的较少了效率
综上:建堆选择向下调整法,时间复杂度是O(N),堆排序时间复杂度是O(N*logN)
九月:祝你我渐入佳境。

























 5565
5565











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








