练习题（2024/5/4）

最新推荐文章于 2025-05-27 10:55:24 发布

@干吧jyb

最新推荐文章于 2025-05-27 10:55:24 发布

阅读量723

点赞数 7

文章标签： java 前端 javascript leetcode 算法数据结构

本文链接：https://blog.csdn.net/m0_74859128/article/details/138451573

版权

1 二叉树的所有路径

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

示例 1：

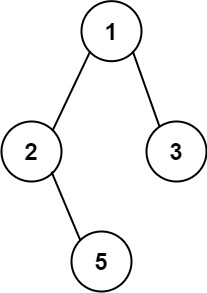
输入：root = [1,2,3,null,5]
输出：["1->2->5","1->3"]

示例 2：

输入：root = [1]
输出：["1"]

提示：

树中节点的数目在范围 [1, 100] 内
-100 <= Node.val <= 100

思路：

通过递归遍历二叉树的方式来实现。

第一步是确定递归函数的参数和返回值。在这里，递归函数的参数包括当前节点cur、当前路径path以及存储结果的容器result，返回值为void类型。

第二步是确定递归函数的结束条件。在这里，当当前节点为叶子节点时，即左右子节点都为空时，将当前路径添加到结果集中并返回。

第三步是确定递归函数的单层递归逻辑。在这里，我们首先将当前节点的值添加到路径中，然后分别向左子树和右子树递归遍历。当向左子树遍历时，将当前路径加上“->”作为路径传入递归函数中；同样，当向右子树遍历时，也是将当前路径加上“->”作为路径传入递归函数中。

最后，在主函数中通过调用递归函数，从根节点开始递归遍历二叉树，将所有根节点到叶子节点的路径添加到结果集中并返回结果。

代码：

class Solution {
private:
    // 递归遍历二叉树
    void traversal(TreeNode* cur, string path, vector<string>& result) {
        // 将当前节点的值添加到路径中
        path += to_string(cur->val);
        // 如果当前节点是叶子节点，将路径添加到结果集中并返回
        if (cur->left == nullptr && cur->right == nullptr) {
            result.push_back(path);
            return;
        }
        // 向左子树遍历
        if (cur->left) {
            string leftPath = path + "->";
            traversal(cur->left, leftPath, result); // 左
        }
        // 向右子树遍历
        if (cur->right) {
            string rightPath = path + "->";
            traversal(cur->right, rightPath, result); // 右
        }
    }
public:
    // 获取二叉树所有根节点到叶子节点的路径
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> result;
        if (root == nullptr) {
            return result;
        }
        string path; // 初始化路径为空
        traversal(root, path, result); // 从根节点开始递归遍历
        return result;
    }
};

`2`相同的树

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

示例 1：

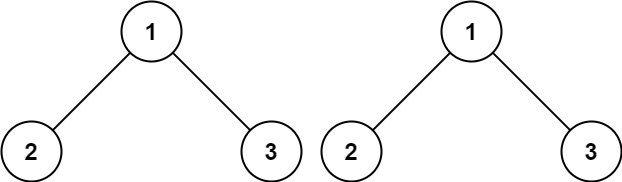
输入：p = [1,2,3], q = [1,2,3]
输出：true

示例 2：

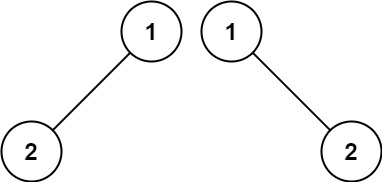
输入：p = [1,2], q = [1,null,2]
输出：false

示例 3：

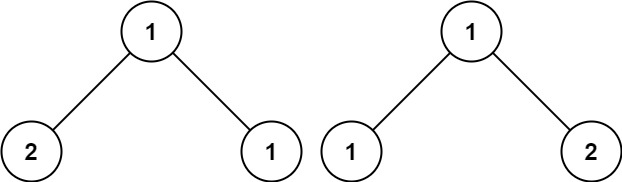
输入：p = [1,2,1], q = [1,1,2]
输出：false

提示：

两棵树上的节点数目都在范围 [0, 100] 内
-104 <= Node.val <= 104

思路：

使用递归来判断两棵树是否相同。首先判断特殊情况，如果两个节点都为空，则返回true；如果一个节点为空另一个节点不为空，则返回false；如果两个节点的值不相同，则返回false。然后递归判断两个节点的左子树和右子树是否相同，最终返回判断结果。

代码：

class Solution {
public:
    // 判断两棵树是否相同
    bool isSameTree(TreeNode* p, TreeNode* q) {
        // 如果两个节点均为空，则相同
        if (p == nullptr && q == nullptr) {
            return true;
        }
        // 如果一个节点为空，另一个不为空，则不相同
        else if (p == nullptr || q == nullptr) {
            return false;
        }
        // 如果节点值不相同，则不相同
        else if (p->val != q->val) {
            return false;
        }
        // 递归判断左右子树是否相同
        else {
            return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
        }
    }
};

`3`另一棵树的子树

给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。

二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

示例 1：

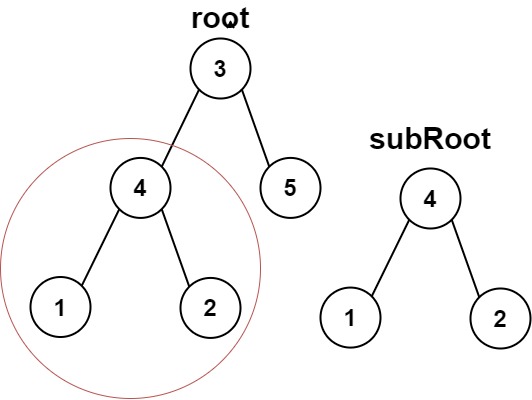
输入：root = [3,4,5,1,2], subRoot = [4,1,2]
输出：true

示例 2：

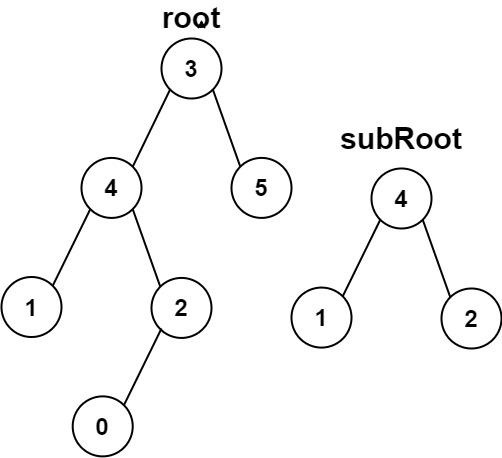
输入：root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
输出：false

提示：

root 树上的节点数量范围是 [1, 2000]
subRoot 树上的节点数量范围是 [1, 1000]
-104 <= root.val <= 104
-104 <= subRoot.val <= 104

思路：

使用isSameTree函数来判断两棵树是否相同，这个函数要判断两棵树是否有相同的结构和节点值。然后在isSubtree函数中，我们逐个检查给定树的所有节点，看是否存在与给定子树相同的子树。如果当前节点与给定子树相同，则直接返回true；否则递归检查左子树和右子树，直到找到相同的子树或遍历完整个树。整个过程就是利用递归的方式不断向下查找相同的子树，利用isSameTree函数来确定子树是否相同。

代码：

class Solution {
public:
    // 判断两棵树是否相同
    bool isSameTree(TreeNode* p, TreeNode* q) {
        if (p == nullptr && q == nullptr) // 如果两个节点均为空，则相同
            return true;
        if (p == nullptr || q == nullptr) // 如果一个节点为空另一个节点不为空，则不相同
            return false;
        if (p->val != q->val) // 如果两个节点的值不相同，则不相同
            return false;
        // 递归判断左右子树是否相同
        return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
    }
    // 判断是否为子树
    bool isSubtree(TreeNode* root, TreeNode* subRoot) {
        if (root == nullptr) // 如果根节点为空，无法比较子树
            return false;
        bool flag = isSameTree(root, subRoot); // 判断当前节点与子树是否相同
        if (flag) // 如果相同，则直接返回true
            return true;
        // 否则递归检查左子树和右子树
        return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
    }
};

4排名靠前的旅行者

表：Users

+---------------+---------+
| Column Name   | Type    |
+---------------+---------+
| id            | int     |
| name          | varchar |
+---------------+---------+
id 是该表中具有唯一值的列。
name 是用户名字。

表：Rides

+---------------+---------+
| Column Name   | Type    |
+---------------+---------+
| id            | int     |
| user_id       | int     |
| distance      | int     |
+---------------+---------+
id 是该表中具有唯一值的列。
user_id 是本次行程的用户的 id, 而该用户此次行程距离为 distance 。

编写解决方案，报告每个用户的旅行距离。

返回的结果表单，以 travelled_distance 降序排列 ，如果有两个或者更多的用户旅行了相同的距离, 那么再以 name 升序排列 。

返回结果格式如下例所示。

示例 1：

输入：
Users 表：
+------+-----------+
| id   | name      |
+------+-----------+
| 1    | Alice     |
| 2    | Bob       |
| 3    | Alex      |
| 4    | Donald    |
| 7    | Lee       |
| 13   | Jonathan  |
| 19   | Elvis     |
+------+-----------+

Rides 表：
+------+----------+----------+
| id   | user_id  | distance |
+------+----------+----------+
| 1    | 1        | 120      |
| 2    | 2        | 317      |
| 3    | 3        | 222      |
| 4    | 7        | 100      |
| 5    | 13       | 312      |
| 6    | 19       | 50       |
| 7    | 7        | 120      |
| 8    | 19       | 400      |
| 9    | 7        | 230      |
+------+----------+----------+
输出：
+----------+--------------------+
| name     | travelled_distance |
+----------+--------------------+
| Elvis    | 450                |
| Lee      | 450                |
| Bob      | 317                |
| Jonathan | 312                |
| Alex     | 222                |
| Alice    | 120                |
| Donald   | 0                  |
+----------+--------------------+
解释：
Elvis 和 Lee 旅行了 450 英里，Elvis 是排名靠前的旅行者，因为他的名字在字母表上的排序比 Lee 更小。
Bob, Jonathan, Alex 和 Alice 只有一次行程，我们只按此次行程的全部距离对他们排序。
Donald 没有任何行程, 他的旅行距离为 0。

思路：

从用户表和骑行记录表进行左连接，根据用户ID进行连接，并按用户ID分组。然后计算每个用户的行驶距离，如果没有行驶记录则将距离设置为0。最后按行驶距离降序排序，并按用户名升序排序，从而得到每位用户的行驶距离情况。

在 SQL 中，IFNULL 是一个函数，用于处理 NULL 值。IFNULL 函数接受两个参数，如果第一个参数不为 NULL，则返回第一个参数的值；如果第一个参数为 NULL，则返回第二个参数的值

代码：

select name,ifnull(sum(distance),0) travelled_distance  
from users left join rides 
on users.id = rides.user_id 
group by user_id 
order by sum(distance) desc,name