小掰笔记之：回溯算法详解（超长的哦！）

小掰是苣蒻

已于 2023-11-02 23:12:13 修改

阅读量1.1k

点赞数 25

分类专栏：数据结构与算法文章标签：算法 java 回归算法深度优先遍历

于 2023-11-02 23:10:27 首次发布

本文链接：https://blog.csdn.net/m0_74984806/article/details/134172153

版权

数据结构与算法专栏收录该内容

2 篇文章 0 订阅

订阅专栏

系列文章目录

这里是小掰第一次写博客，主要是对平时学习的内容进行一个总结（相当于个人笔记了），欢迎大佬们指出我的错误与不足，希望各位同学共勉！！！

本文详细内容参考代码随想录，感谢卡尔哥和各位贡献者给广大新手提供了这么一个好网站。

！连接在这里代码随想录.回溯算法！

前言

可能很多同学上数据结构与算法课的时候都会听到类似的话“当我们遍历到这个节点之后，对这个节点进行。。。操作，然后再回溯到上一个状态，更新。。。”
这个时候就会有同学问：什么是回溯？为什么要回溯？怎么进行回溯？ 接下来就让小掰来带你一文看懂回溯算法。（记得做笔记哦）

一、什么是回溯算法？

回溯法也可以叫做回溯搜索法，它是一种搜索的方式。但这种算法的本质其实是穷举。

学习过树或图结构的同学们应该学过一种很重要的算法 DFS（深度优先搜索），其实DFS和回溯算法可以算是父子关系，他们都蕴含了“不撞南墙不回头”的思想

DFS是能够在图结构里搜索到通往特定终点的一条或者多条特定路径
回溯法是能够在树结构里搜索到通往特定终点的一条或者多条特定路径

我们知道树结构是图结构的一种，回溯法以深度优先搜索的方式搜索解空间，并且在搜索过程中用剪枝函数避免无效搜索

因而我们暂时可以简单的理解为回溯 = DFS + 剪枝函数
（为什么说暂时？请看此文回溯算法与DFS的区别，本文就不展开讨论了）

在题目二叉树的所有路径中，我们使用DFS遍历到叶子节点后就将整条路径添加到输出容器中，而这个解题方法里面就蕴含着回溯的思想。（建议先简单看完以下内容，完整阅读本文后再回顾此题！）

"""
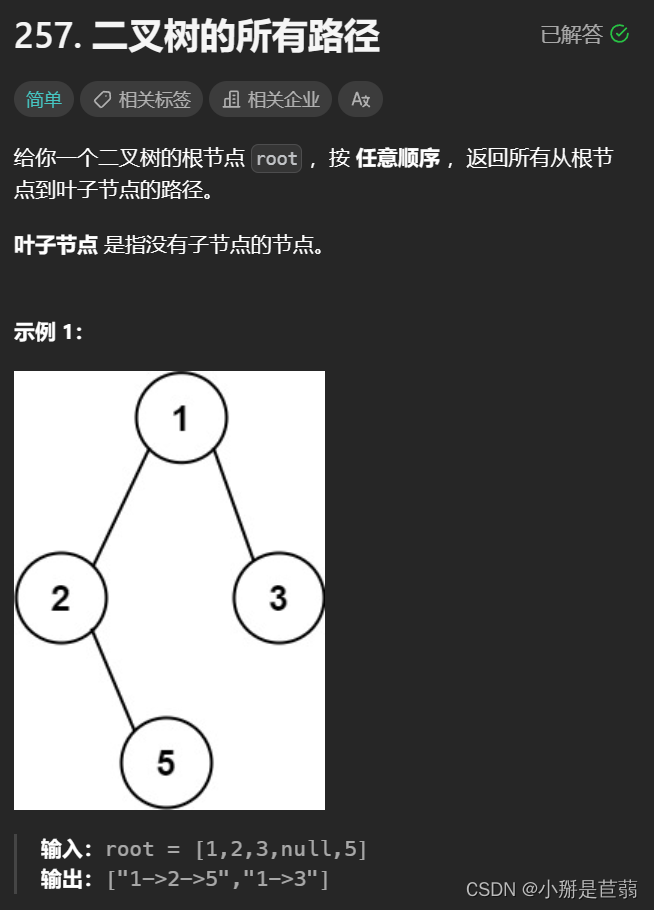
这题的回溯其实是隐藏起来了的，也就是说，虽然我们用到了回溯，
但是我们并没有将回溯的特征代码写出来
如果写出来就是
if (cur->left) {
    path += "->";
    traversal(cur->left, path, result); // 左
    path.pop_back(); // 回溯，抛掉val
    path.pop_back(); // 回溯，抛掉->
}
if (cur->right) {
    path += "->";
    traversal(cur->right, path, result); // 右
    path.pop_back(); // 回溯（非必要）
    path.pop_back(); 
}
但是由于path是作为一个参数出现在traversal方法里面的，而不是全局变量
所以我们可以直接对本层的path进行修改,这样并不会对上一层的path造成影响
不需要撤销上一次操作（这里相当于自动销毁了）
同时也不需要使用result.add(new LinkedList<>(path));
"""
class Solution {
  public void traversal(TreeNode cur, String path, List<String> result) {
      path += cur.val; // 中
      if (cur.left == null && cur.right == null) {
          result.add(path);
          return;
      }
      if (cur.left!=null) traversal(cur.left, path + "->", result); // 左  回溯就隐藏在这里
      if (cur.right!=null) traversal(cur.right, path + "->", result); // 右 回溯就隐藏在这里
  }

  public List<String> binaryTreePaths(TreeNode root) {
      List<String> result = new LinkedList<>();
      String path = "";
      if (root == null) return result;
      traversal(root, path, result);
      return result;
  }
}

二、为什么要使用回溯算法？

回溯法，一般可以解决如下几种问题：

组合问题：N个数里面按一定规则找出k个数的集合
切割问题：一个字符串按一定规则有几种切割方式
子集问题：一个N个数的集合里有多少符合条件的子集
排列问题：N个数按一定规则全排列，有几种排列方式
棋盘问题：N皇后，解数独等等

相信大家看着这些之后会发现，每个问题，都不简单！

那么我们使用回溯法能快速高效解决这类问题吗？答案是不能。。

因为回溯的本质是穷举，穷举所有可能，然后选出我们想要的答案，如果想让回溯法高效一些，可以加一些剪枝的操作，但也改不了回溯法就是穷举的本质。

那么既然回溯法并不高效为什么还要用它呢？

因为没得选，这些问题能暴力搜出来就不错了，撑死了再剪枝一下，还没有更高效的解法。

三、怎么使用回溯算法？

首先我们要理解回溯算法的基本原理：将问题抽象为树形结构，通过纵向递归遍历，横向循环遍历，寻找问题的答案。

例如：

大家可以从图中看出for循环可以理解是横向遍历，backTrace（递归）就是纵向遍历，这样就把这棵树全遍历完了，一般来说，搜索叶子节点就是找的其中一个结果了。

既然知道了基本原理，那我们可以给回溯算法写出一个基本模版

public void backTrace(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backTracke(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

学会了基础模版之后，我们就可以开始刷力扣题了，接下来我会对我觉得具有代表性的题目做一个具体分析。

四、应用

1.组合

传送门在这里~

这道题是经典的回溯算法题，我们可以将本题抽象为以下树结构

可以看出这棵树，一开始集合是 1，2，3，4，从左向右取数，取过的数，不再重复取。

第一次取1，集合变为2，3，4 ，因为k为2，我们只需要再取一个数就可以了，分别取2，3，4，得到集合[1,2] [1,3] [1,4]，以此类推。

每次从集合中选取元素，可选择的范围随着选择的进行而收缩，调整可选择的范围。

图中可以发现n相当于树的宽度，k相当于树的深度。

那么如何在这个树上遍历，然后收集到我们要的结果集呢？

图中每次搜索到了叶子节点，我们就找到了一个结果。

相当于只需要把达到叶子节点的结果收集起来，就可以求得 n个数中k个数的组合集合。

那么我们就可以根据模版开始编写代码了：

List<List<Integer>> ans = new ArrayList<>();
List<Integer> temp = new ArrayList<>();
public void backTrace(int n, int k, int startIndex) {
    //
}

这里我们将最终返回的结果与临时存储的结果都使用全局变量，因为这样可以减少backtrace()方法里面的参数，增加代码的可读性。

startIndex参数是我们在方法体内的for循环需要使用的，给 i 赋值，控制循环开头的数字,防止出现重复的组合。从下图中红线部分可以看出，在集合[1,2,3,4]取1之后，下一层递归，就要在[2,3,4]中取数了，那么下一层递归如何知道从[2,3,4]中取数呢，靠的就是startIndex。

那么既然是递归，我们就必须先确定递归的终止条件，这里我们判断递归终止的条件就是到达叶子节点，那怎么判断是否到达叶子节点呢？

如果temp这个临时存储数组的大小如果达到k，说明我们找到了一个子集大小为k的组合了，在图中temp存的就是根节点到叶子节点的路径。

代码如下：

if(temp.size() == k) {
    ans.add(new ArrayListList<>(temp));
    return;
}
"""
注意这里的ans.add(new ....);
这是因为我们将temp设定为一个全局变量，
如果ans.add(temp);
最后我们回溯会对temp这个对象造成影响，
也就是会对ans存放的temp进行修改，
所以我们必须new一个新的对象，再将数据存进ans里面
"""

那backTrace方法的剩余部分，就是对非叶子节点的节点数据进行处理的操作

利用for循环每次从startIndex开始遍历，然后用temp保存取到的节点i

代码如下：

for(int i = startIndex; i <= n - (k - temp.size()) + 1; i++){// 控制树的横向遍历
    temp.add(i);// 处理节点
    backTrace(n, k, i + 1);// 递归：控制树的纵向遍历，注意下一层搜索要从i+1开始
    temp.remove(temp.size() - 1);// 回溯，撤销处理的节点
}

那么我们就可以写出完整的代码了：

class Solution {
    public List<List<Integer>> ans = new ArrayList<>();//存放结果
    public List<Integer> temp = new ArrayList<>();//暂时存放数据
    
    public void backTrace(int n, int k, int startIndex){
        if(temp.size() == k){ //到达叶子节点
            ans.add(new ArrayList<>(temp));//将数据填充到ans
            return;//递归结束
        }

        for(int i = startIndex; i <= n - (k - temp.size()) + 1; i++){// 控制树的横向遍历
            temp.add(i);// 处理节点
            backTrace(n, k, i + 1);// 递归：控制树的纵向遍历，注意下一层搜索要从i+1开始
            temp.remove(temp.size() - 1);// 回溯，撤销处理的节点
        }

    }
    public List<List<Integer>> combine(int n, int k) {
        backTrace(n, k, 1);
        return ans;
    }

}

回溯法虽然是暴力搜索，但也有时候可以剪枝优化

什么是剪枝呢？我们直接上原图：

我们把哪些明显不符合条件的节点分支去掉，即不遍历这个分支，这样就达到了我们减少时间消耗的目的。

图中每一个节点，就代表本层的一个for循环，那么每一层的for循环从第二个数开始遍历的话，都没有意义，都是无效遍历。

所以，可以剪枝的地方就在递归中每一层的for循环所选择的起始位置。

如果for循环选择的起始位置之后的元素个数已经不足我们需要的元素个数了，那么就没有必要搜索了。

接下来看一下优化过程如下：

已经选择的元素个数：temp.size();
还需要的元素个数为: k - temp.size();
在集合n中至多要从该起始位置 : n - (k - temp.size()) + 1，开始遍历

所以优化之后的for循环是：

for (int i = startIndex; i <= n - (k - temp.size()) + 1; i++) // i为本次搜索的起始位置

总体代码就是：

class Solution {
    List<List<Integer>> ans = new ArrayList<>();
    LinkedList<Integer> temp = new ArrayList<>();
    public List<List<Integer>> combine(int n, int k) {
        backTrace(n, k, 1);
        return ans;
    }

    /**
     * 每次从集合中选取元素，可选择的范围随着选择的进行而收缩，调整可选择的范围，就是要靠startIndex
     * @param startIndex 用来记录本层递归的中，集合从哪里开始遍历（集合就是[1,...,n] ）。
     */
    private void backTrace(int n, int k, int startIndex){
        //终止条件
        if (temp.size() == k){
            ans.add(new ArrayList<>(temp));
            return;
        }
        for (int i = startIndex; i <= n - (k - temp.size()) + 1; i++){
            temp.add(i);
            backTrace(n, k, i + 1);
            temp.remove(temp.size() - 1);
        }
    }
}

（请同学们注意，在我们学习回溯算法的时候一定要注意纵向和横向遍历区别，自己可以在草稿本上模拟一下递归的过程，因为在后面我们要编写剪枝方法的时候就会出现横向使用过或纵向使用过的判断。）

2.组合总和II

传送门在这里~

我们在第一题学会了使用回溯的模版和剪枝方法的编写，而这道题就教会我们如何去重。

本题的难点在于数组 candidates 有重复元素，但还不能有重复的组合。

如果使用HashSet或者是HashMap容易导致超时，所以我们必须在搜索的过程中就将它去重。

都知道组合问题可以抽象为树形结构，那么“使用过”在这个树形结构上是有两个维度的，一个维度是同一树枝上使用过，一个维度是同一树层上使用过。没有理解这两个层面上的“使用过” 是造成大家没有彻底理解去重的根本原因。

那么问题来了，我们是要同一树层上使用过，还是同一树枝上使用过呢？

回看一下题目，元素在同一个组合内是可以重复的，怎么重复都没事，但两个组合不能相同。

所以我们要去重的是同一树层上的“使用过”，同一树枝上的都是一个组合里的元素，不用去重。

划重点了！！！！！

我们强调 树层上的使用过 与 树枝上的使用过 是需要不同对待的

（树层去重的话，需要对数组排序！）

那么怎么去存储相同的多个数字在树层上的使用过和树枝上的使用过这两个信息呢？

聪明的小伙伴可能就想到了数据类型里面，boolean型可以完美的存储这两个信息。

那么话不多说，我么直接看代码：

List<List<Integer>> ans = new ArrayList<>();
List<Integer> temp = new ArrayList<>();
boolean[] used;

(这里我们使用一个used数组，用false表示同一树层未使用,true表示同一树层使用过)

递归的终止条件：

if (sum == target) {
    ans.add(new ArrayList(temp));
    return;
}

理解used数组：（这部分我直接上卡尔哥的原文了）

前面我们提到：要去重的是“同一树层上的使用过”，如何判断同一树层上元素（相同的元素）是否使用过了呢。

如果candidates[i] == candidates[i - 1] 并且 used[i - 1] == false，就说明：前一个树枝，使用了candidates[i - 1]，也就是说同一树层使用过candidates[i - 1]。

此时for循环里就应该做continue的操作。

这块比较抽象，如图：

我在图中将used的变化用橘黄色标注上，可以看出在candidates[i] == candidates[i - 1]相同的情况下：

used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
used[i - 1] == false，说明同一树层candidates[i - 1]使用过

可能有的录友想，为什么 used[i - 1] == false 就是同一树层呢，因为同一树层，used[i - 1] == false 才能表示，当前取的 candidates[i] 是从 candidates[i - 1] 回溯而来的。

而 used[i - 1] == true，说明是进入下一层递归，去下一个数，所以是树枝上，如图所示：

（这里我放原文的原因是因为我看了网上讲解那么多关于回溯去重的文章，只有卡尔哥讲得最到位，最容易理解，%这里是原文%，希望大家积极思考，理解通透这种方法。）

结合以上内容，那么我们就可以写出以下代码：

class Solution {
    List<Integer> temp = new ArrayList<>(); // 存储当前组合
    List<List<Integer>> ans = new ArrayList<>(); // 存储所有有效的组合
    boolean[] used; // 记录数字是否在当前树层中被使用
    int sum = 0; // 当前组合的总和

    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        used = new boolean[candidates.length]; // 将used数组初始化为所有false值
        Arrays.fill(used, false);
        Arrays.sort(candidates); // 对数组进行排序，以便将重复的数字放在一起
        backTracking(candidates, target, 0); // 调用回溯函数来找到组合
        return ans; // 返回组合的列表
    }


    private void backTracking(int[] candidates, int target, int startIndex) {
        if (sum == target) { // 如果当前组合的总和等于目标值
            ans.add(new ArrayList<>(temp)); // 将组合添加到有效组合的列表中
            return;
        }
        for (int i = startIndex; i < candidates.length; i++) { // 遍历树层
            if (sum + candidates[i] > target) { // 如果把当前数字加入总和超过目标值
                break; // 停止探索该分支(剪枝)
            }
            if (i > startIndex && candidates[i] == candidates[i - 1] && !used[i - 1]) {
                // 去重
                continue;
            }
            used[i] = true; // 将当前数字标记为已使用
            sum += candidates[i]; // 加入总和
            temp.add(candidates[i]); // 将当前数字添加到组合中
            backTracking(candidates, target, i + 1); // 递归地探索下一个
            //回溯后
            used[i] = false; // 将当前标记为未使用
            sum -= candidates[i]; // 从总和中减去当前数字
            temp.remove(temp.size() - 1); // 从组合中移除当前数字
        }
    }
}

3.分割回文串

传送门在这里~

本题这涉及到两个关键问题：

切割问题，有不同的切割方式
判断回文

所以我们要编写两个方法，一个用于回溯，一个用于判断子串是否回文

首先我们先将本题抽象为一个树结构：

递归用来纵向遍历，for循环用来横向遍历，切割线（就是图中的红线）切割到字符串的结尾位置，说明找到了一个切割方法。

来看看在递归循环中如何截取子串呢？

在for( int i = stIndex; i < s.length(); i++ )循环中，我们定义了起始位置stIndex，那么 [stIndex, i] 就是要截取的子串。

首先判断这个子串是不是回文，如果是回文，就加入在List<String> temp中，temp用来记录切割过的回文子串。

那么本题就可以按照前面两题简单地写出以下代码：

class Solution {
    // 用于存储所有可能的分割结果的列表
    List<List<String>> ans = new ArrayList<>();
    // 用于存储当前分割结果的列表
    List<String> temp = new ArrayList<>();


    public List<List<String>> partition(String s) {

        traceBack(s, 0);

        return ans;
    }


    public void traceBack(String s, int stIndex) {
        // 如果起始索引大于等于字符串的长度，表示已经遍历完整个字符串，找到了一个有效的分割结果
        if(stIndex >= s.length()) {
            // 将当前分割结果添加到所有分割结果的列表中
            ans.add(new ArrayList<>(temp));
            // 返回以继续回溯过程
            return;
        }

        // 从给定索引开始遍历字符串
        for( int i = stIndex; i < s.length(); i++ ) {
            // 检查从起始索引到当前索引的子串是否是回文串
            if (isPalindrome(s, stIndex, i)) {
                // 如果是回文串，将其添加到当前分割结果中
                temp.add(s.substring(stIndex, i + 1));

            }else {
                // 如果不是回文串，继续下一次遍历
                continue;
            }
            // 继续回溯过程，以下一个索引作为起始索引
            traceBack(s, i + 1);
            // 回溯时移除最后添加的回文串
            temp.remove(temp.size() - 1);
        }
    }


    public boolean isPalindrome(String s, int startIndex, int end) {
        // 从两端开始遍历子串
        for (int i = startIndex, j = end; i < j; i++, j--) {
            // 如果当前索引处的字符不相等，则不是回文串
            if (s.charAt(i) != s.charAt(j)) {
                return false;
            }
        }
        // 如果所有字符都相等，则是回文串
        return true;
    }
}

完成这题之后，你可以选择尝试一下复原IP地址这道题，也是使用回溯算法对分割字符串的应用，不过这道题的技巧和剪枝方法要更复杂一点。

4.子集II

传送门在这里~

关于回溯算法中的去重问题，在组合总和II 中已经详细讲解过了，和本题是一个套路。

而且排列问题里去重也是这个套路，所以理解“树层去重”和“树枝去重”非常重要。

用示例中的[1, 2, 2] 来举例，如图所示：（注意去重需要先对集合排序）

和组合总和II 一样，我们只要将同一树层的相同元素进行去重，而同一树枝上的相同元素保留即可，但是，这道题我希望我们可以不使用used数组来实现。

不使用used数组，我们怎么完成去重操作呢？

其实很简单，只需要在for循环里面添加两行代码即可。

if (i > stIndex && nums[i] == nums[i - 1] ) {
	continue;
}

因为是在for循环（横向遍历）的过程中，所以就可以去掉同一树层的相同元素

那么代码就是：

class Solution {
    public List<List<Integer>> ans = new ArrayList<>();
    public List<Integer> temp = new ArrayList<>();
    public List<List<Integer>> subsetsWithDup(int[] nums) {
        Arrays.sort(nums);
        traceBack(nums, 0);
        return ans;
    }

    public void traceBack(int[] nums, int stIndex) {
        ans.add(new ArrayList<>(temp));

        for(int i = stIndex; i < nums.length; i++) {
            if (i > stIndex && nums[i] == nums[i - 1]) {
                continue;
            }
            temp.add(nums[i]);
            traceBack(nums, i + 1);
            temp.remove(temp.size() - 1);
        }
    }
}

当然，本题还有另一种解法：

class Solution {
    List<Integer> temp = new ArrayList<>();
    List<List<Integer>> ans = new ArrayList<>();

    public List<List<Integer>> subsetsWithDup(int[] nums) {
        Arrays.sort(nums);
        backTrace(0, nums);
        return ans;
    }

    public void backTrace(int i, int[] nums) {
        if (i == nums.length) {
            ans.add(new ArrayList<>(temp));
            return;
        }
        temp.add(nums[i]);
        backTrace(i + 1, nums);
        temp.remove(temp.size() - 1);

        // 不选就跳过后面一样的数，只需要用【78. 子集】的代码加这两行就搞定了！
        while (i + 1 < nums.length && nums[i + 1] == nums[i])
            i++;

        backTrace(i + 1, nums);
    }
}

这种写法采用了更高效的去重方式，while循环的目的是跳过重复的元素。在循环结束后，索引i指向当前元素的最后一个出现位置。通过调用backTrace(i + 1, nums)，我们继续处理数组中的下一个唯一元素，并继续回溯过程。这样可以确保我们生成的所有子集都是没有重复元素的。

5.递增子序列

这个递增子序列比较像是取有序的子集。而且本题也要求不能有相同的递增子序列。

这又是子集，又是去重，是不是不由自主的想起了刚刚讲过的子集II。

就是因为太像了，更要注意差别所在，要不就掉坑里了！

在子集II中我们是通过排序，再加一个标记数组来达到去重的目的。

而本题求自增子序列，是不能对原数组进行排序的，排完序的数组都是自增子序列了。

所以不能使用之前的去重逻辑！

先举个例子，模拟一下本题的运行思路：

我们可以看到，在树层上，我们的去重思路还是一样的，但是在树枝上，我们不仅要去重，还要考虑接下来取的这个数字是否大于上一个数字

根据以上逻辑，我们可以写出：

private void backTrace(int[] nums, int stIndex) {
        //递增序列的长度必须大于等于2
        if(temp.size() >= 2) ans.add(new ArrayList<>(temp)); 
        //使用哈希表来存储本层使用过的数字           
        HashSet<Integer> hs = new HashSet<>();
        for(int i = stIndex; i < nums.length; i++){
        //去重
        if(!temp.isEmpty() && temp.get(temp.size() -1 ) > nums[i] || 
hs.contains(nums[i]) continue;
        //回溯几步走
        hs.add(nums[i]);
        temp.add(nums[i]);
        backTrace(nums, i + 1);
        temp.remove(temp.size() - 1);
    }
}

完成了单层搜索的代码，整个部分的代码就可以很轻松的写完了：

class Solution {

    List<List<Integer>> ans = new ArrayList<>();
    List<Integer> temp = new ArrayList<>();
    
    public List<List<Integer>> findSubsequences(int[] nums) {
        backTrace(nums,0);
        return ans;
    }

    public void backTrace(int[] nums, int stIndex) {
        if(temp.size() > 1) {
            ans.add(new ArrayList<>(temp));
        }

        HashSet<Integer> sh = new HashSet<>();
        for(int i = stIndex; i < nums.length; i++) {
            if(!temp.isEmpty() && temp.get(temp.size() - 1) > nums[i] || sh.contains(nums[i])) {
                continue;
            }
            sh.add(nums[i]);
            temp.add(nums[i]); 
            backTrace(nums, i + 1);
            temp.remove(temp.size() - 1);

        }
    }
}

但是这题我的重点并不是这个解法，而是另一位大神的题解：【Java】几乎双百解决 “递增子序列”问题

class Solution {
    private List<List<Integer>> res = new ArrayList<List<Integer>>();
    private List<Integer> temp = new ArrayList<>();

    public List<List<Integer>> findSubsequences(int[] nums) {
        if (nums == null) {
            return null;
        }
        dfs(0, Integer.MIN_VALUE, nums);
        return res;
    }

    private void dfs(int cur, int last, int[] nums) {
        if (cur >= nums.length) {  // 遍历结束
            if (temp.size() >= 2) {
                res.add(new ArrayList<>(temp));
            }
            return;
        }

        if (nums[cur] >= last) {   // 将当前元素加入，并向后遍历
            temp.add(nums[cur]);
            dfs(cur + 1, nums[cur], nums);
            temp.remove(temp.size() - 1);
        }
        if (nums[cur] != last) {   // 不遍历 重复元素
            dfs(cur + 1, last, nums);  // 将下一个元素加入，并向后遍历
        }
    }
}

这种解法的重点思想是：

先将当前元素加入，向后遍历，直到字符串末尾
再将当前元素删除，将后一个元素加入，向后遍历(这里进行了 “剪枝”的判断) 这样就保证了所有不重复子序列都被录入

而我也是用AI帮我模拟了这个代码的运行，请大家自行理解：

以输入数组 nums = [4, 6, 7, 7] 为例，模拟一下代码的运行过程：

首先调用 findSubsequences 方法，将 cur 设为 0，last 设为 Integer.MIN_VALUE，nums 为 [4, 6, 7, 7]。
调用 dfs 方法，传入 cur 为 0，last 为 Integer.MIN_VALUE，nums 为 [4, 6, 7, 7]。
判断 cur 是否等于 nums 的长度，发现不等于，继续执行。
判断 nums[cur] 是否大于等于 last，即 4 是否大于等于 Integer.MIN_VALUE，发现是，将 4 加入 temp 列表中。
调用 dfs 方法，传入 cur 为 1，last 为 4，nums 为 [4, 6, 7, 7]。
判断 cur 是否等于 nums 的长度，发现不等于，继续执行。
判断 nums[cur] 是否大于等于 last，即 6 是否大于等于 4，发现是，将 6 加入 temp 列表中。
调用 dfs 方法，传入 cur 为 2，last 为 6，nums 为 [4, 6, 7, 7]。
判断 cur 是否等于 nums 的长度，发现不等于，继续执行。
判断 nums[cur] 是否大于等于 last，即 7 是否大于等于 6，发现是，将 7 加入 temp 列表中。
调用 dfs 方法，传入 cur 为 3，last 为 7，nums 为 [4, 6, 7, 7]。
判断 cur 是否等于 nums 的长度，发现不等于，继续执行。
判断 nums[cur] 是否大于等于 last，即 7 是否大于等于 7，发现是，将 7 加入 temp 列表中。
判断 temp 的长度是否大于等于 2，即 [4, 6, 7, 7] 是否为一个合法的子序列，发现是，将 [4, 6, 7, 7] 加入 ans 列表中。
回溯到上一层，将 temp 列表中的最后一个元素 7 移除。
回溯到上一层，将 temp 列表中的最后一个元素 7 移除。
判断 nums[cur] 是否等于 last，即 7 是否等于 6，发现不是，继续执行。
调用 dfs 方法，传入 cur 为 3，last 为 6，nums 为 [4, 6, 7, 7]。
判断 cur 是否等于 nums 的长度，发现不等于，继续执行。
判断 nums[cur] 是否大于等于 last，即 7 是否大于等于 6，发现是，将 7 加入 temp 列表中。
判断 temp 的长度是否大于等于 2，即 [4, 6, 7] 是否为一个合法的子序列，发现是，将 [4, 6, 7] 加入 ans 列表中。
回溯到上一层，将 temp 列表中的最后一个元素 7 移除。
回溯到上一层，将 temp 列表中的最后一个元素 6 移除。
判断 nums[cur] 是否等于 last，即 7 是否等于 4，发现不是，继续执行。
调用 dfs 方法，传入 cur 为 2，last 为 4，nums 为 [4, 6, 7, 7]。
判断 cur 是否等于 nums 的长度，发现不等于，继续执行。
判断 nums[cur] 是否大于等于 last，即 7 是否大于等于 4，发现是，将 7 加入 temp 列表中。
判断 temp 的长度是否大于等于 2，即 [4, 7] 是否为一个合法的子序列，发现是，将 [4, 7] 加入 ans 列表中。
回溯到上一层，将 temp 列表中的最后一个元素 7 移除。
判断 nums[cur] 是否等于 last，即 7 是否等于 4，发现不是，继续执行。
调用 dfs 方法，传入 cur 为 2，last 为 4，nums 为 [4, 6, 7, 7]。
判断 cur 是否等于 nums 的长度，发现不等于，继续执行。
判断 nums[cur] 是否大于等于 last，即 7 是否大于等于 4，发现是，将 7 加入 temp 列表中。
判断 temp 的长度是否大于等于 2，即 [4, 7] 是否为一个合法的子序列，发现是，将 [4, 7] 加入 ans 列表中。
回溯到上一层，将 temp 列表中的最后一个元素 7 移除。
回溯到上一层，将 temp 列表中的最后一个元素 6 移除。
回溯到上一层，将 temp 列表中的最后一个元素 4 移除。
最终返回 ans 列表，其中包含了所有的递增子序列 [[4, 6], [4, 7], [4, 6, 7], [4, 6, 7, 7], [6, 7], [6, 7, 7], [7, 7]]。

五、总结

1.本文总结

回溯算法可以算是众多算法里面比较简单的一种算法了，本文以代码随想录为基础，在此之上选出了5道经典题目，用于理解回溯算法的本质，学习编写剪枝方法的技巧，学会将问题抽象为相应结构并解决。

虽然本文对于新手来说并不是很友好，但是有一定算法基础的同学在阅读本文时应该会有一种游戏大佬略微学习就速通的感觉（doge）

有人可能会问为什么经典的N皇后问题没有摆出来，因为本文5道题目都各有各的不同，而不是只要照着模版抄就可以解决的问题。

就好比第一题我们入门了组合问题，学习了回溯算法的基本模版，第二题我们就要解决回溯算法里的去重问题，第三题又到了分割字符串，并且要求我们在回溯的基础上结合其他方法，第四题又回到需要去重的子集问题，第五题则是要求我们真正理解树层和树枝的区别，并且最后我还展示了使用深度优先搜索的解法，这样又让同学们在学习回溯的时候也回顾一下DFS，思考二者之间的区别与联系，加深对于这两种算法的理解（首尾呼应了属于是）。