算法018——在排序数组中查找元素的第一个和最后一个位置

力扣——在排序数组中查找元素的第一个和最后一个位置（点击跳转）

题目中非递减顺序数列说明数组是递增的或者不变的，题目要求查找元素的第一个位置和最后一个位置要找的就是图中的位置

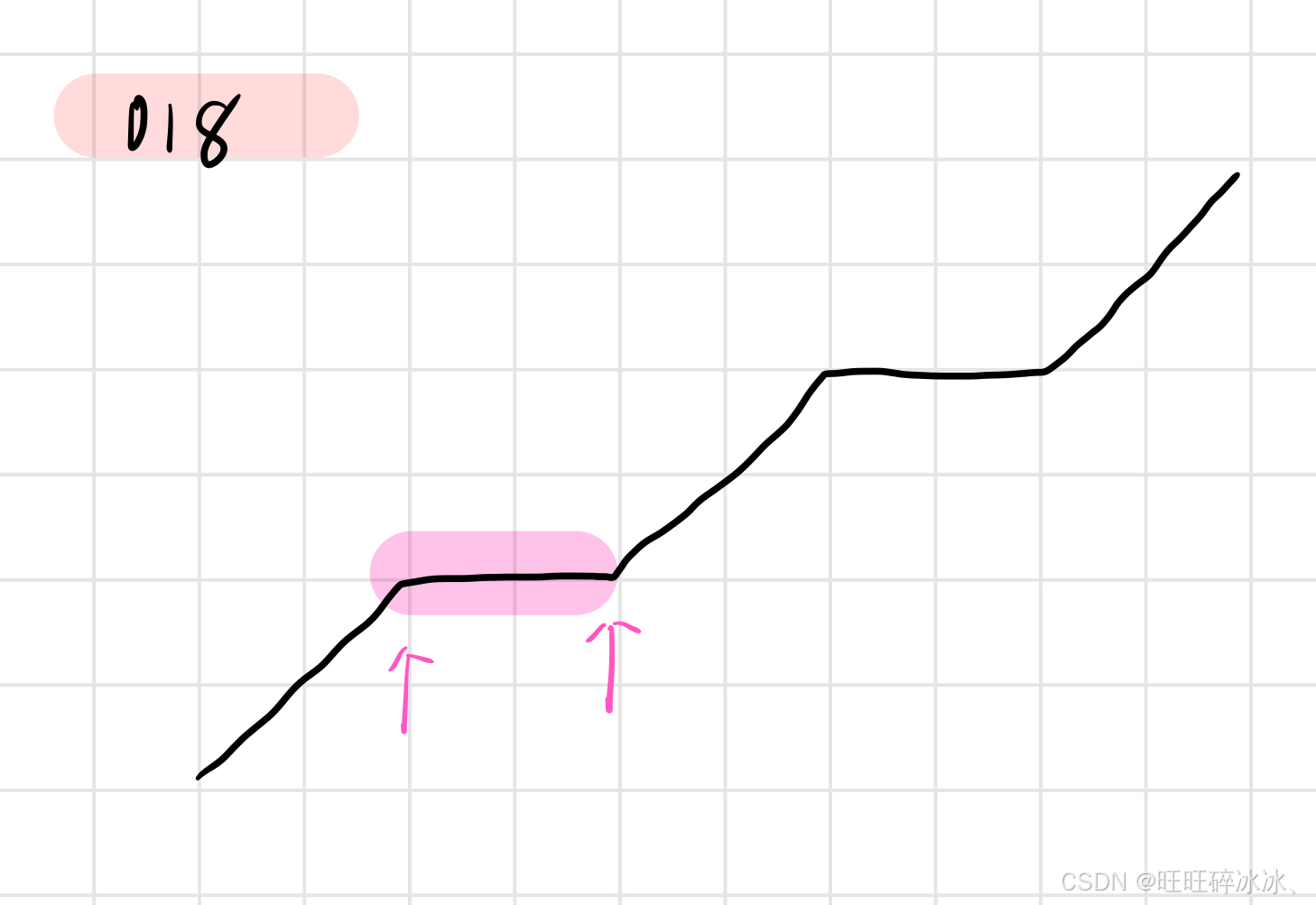
我们的第一想法就是遍历整个数组，然后定义两个变量 begin 和 end 用来存储目标值的起始位置和末尾位置的下标，时间复杂度为 O(N).

假如我们使用普通的二分查找，如果刚开始的 mid 就是目标值，但是我们无法确定目标值究竟在哪个位置，所以普通的二分查找并没有使时间复杂度变小。

我们要利用数组有序这个性质来解决问题，我们可以对二分查找来进行优化从而来解决问题。

我们可以通过二段性来解决问题。

• 查找区间的左端点
  根据左端点我们可以将数组划分为两部分，一部分是左端点前的部分，另一部分是剩下的部分（包括左端点）。
  
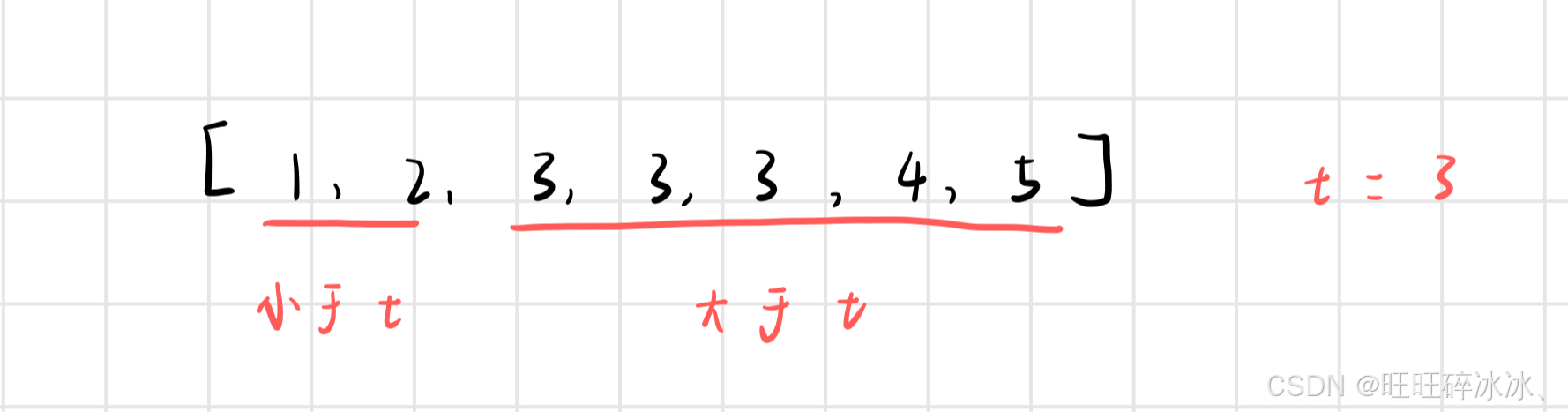
  我们使用二分查找的思想来解决这道题
  
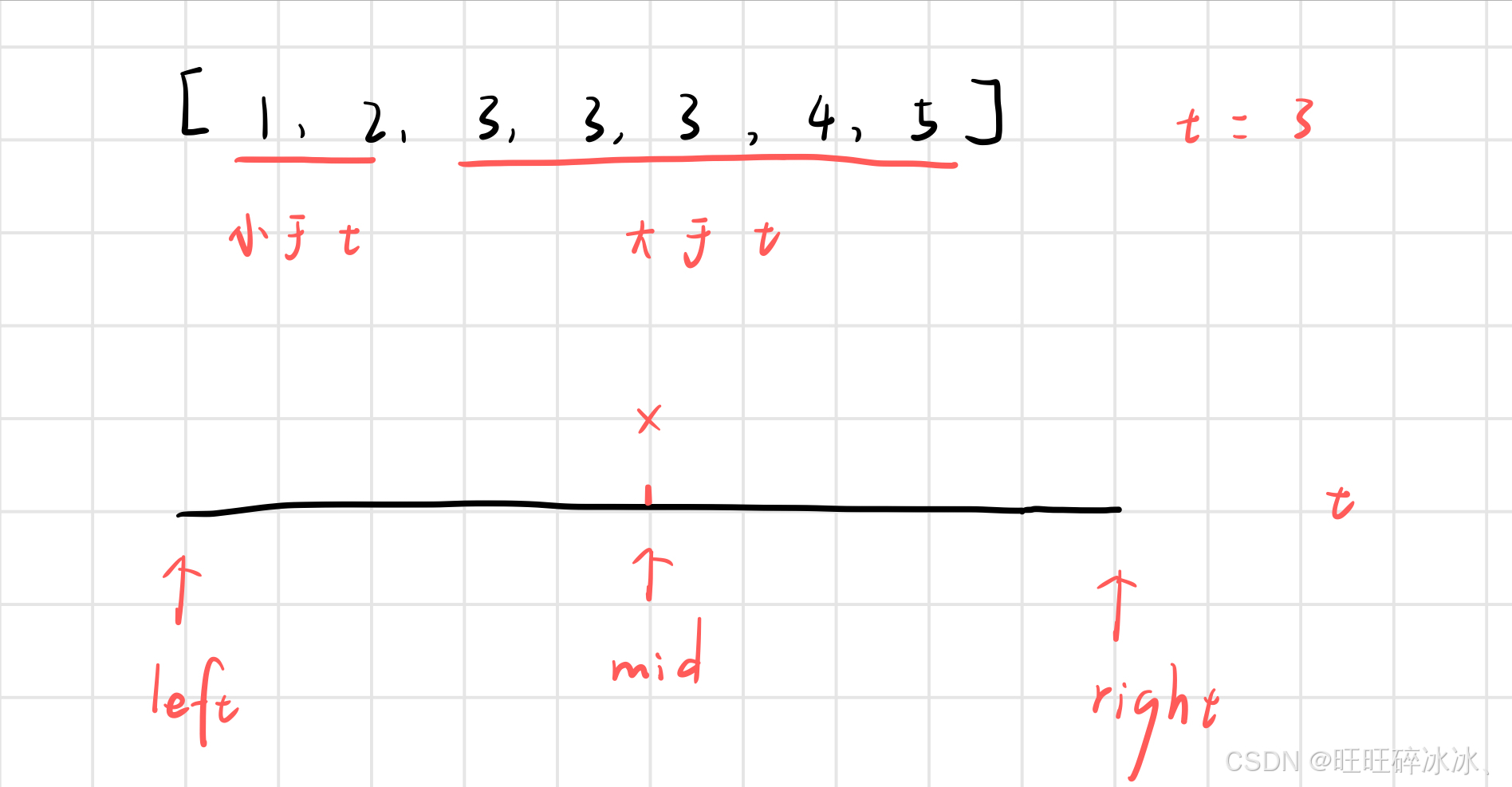
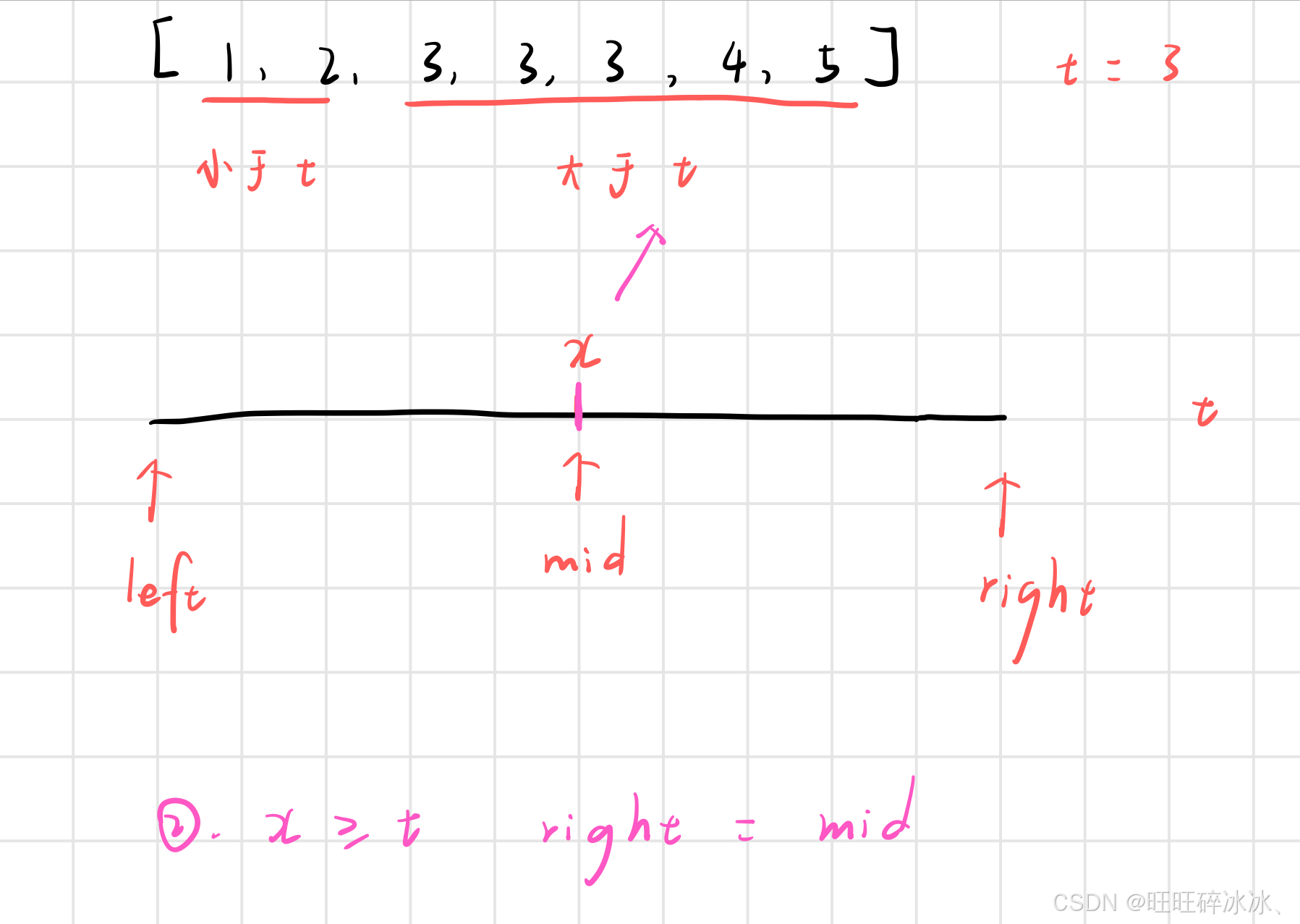
  那么 x 与 t 的关系有三种情况

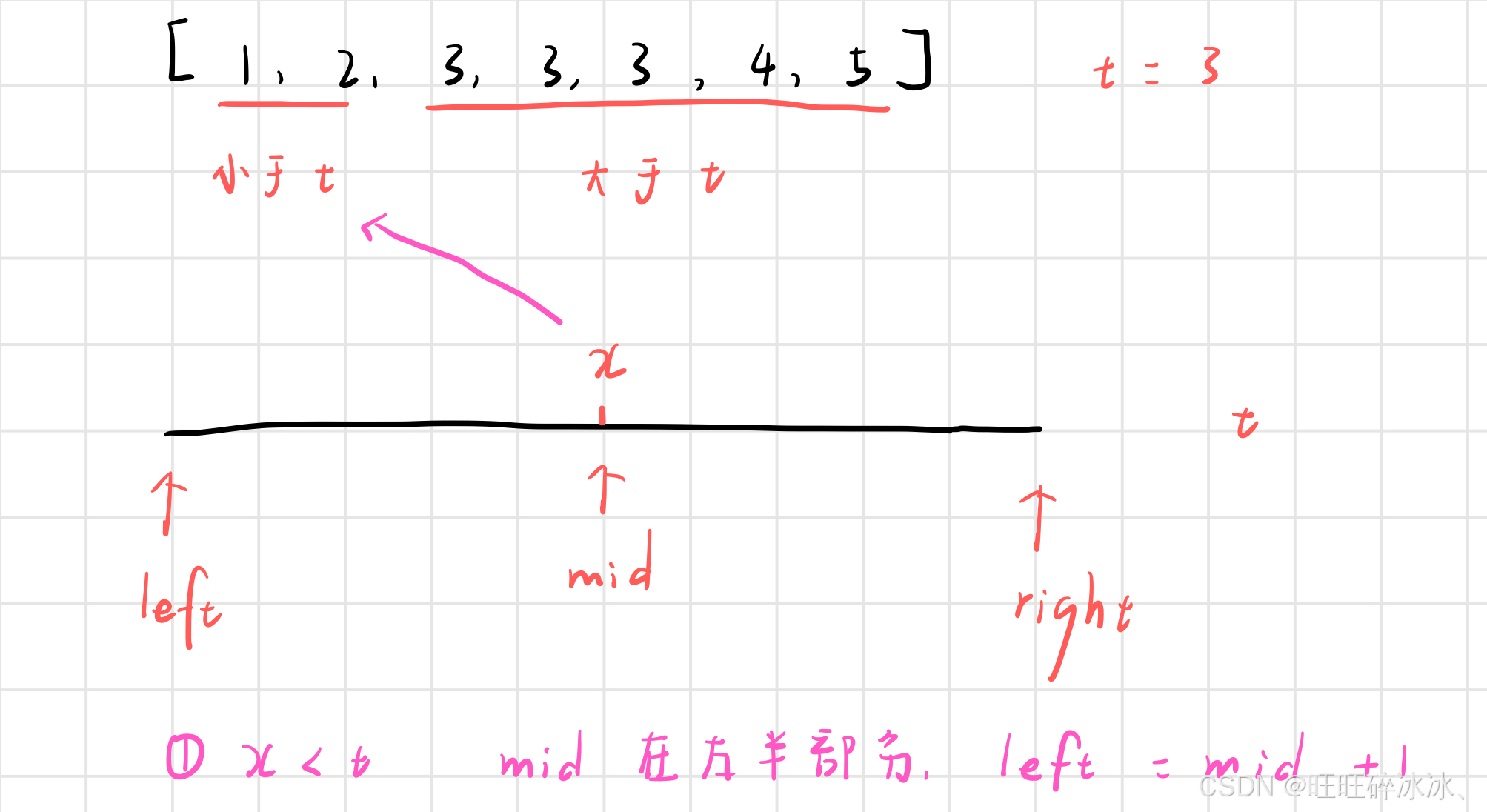
1. x < t
   此时 mid 在左半部分，mid 一定不是目标值，此时让 left = mid + 1，然后在 left 与 right 中继续寻找目标值
   

2. x >= t
   与上一篇普通的二分查找不同的是，此时是 x >= t ，如果将 = 的情况单独拿出来，有可能不是最终的位置，如下图所示
   
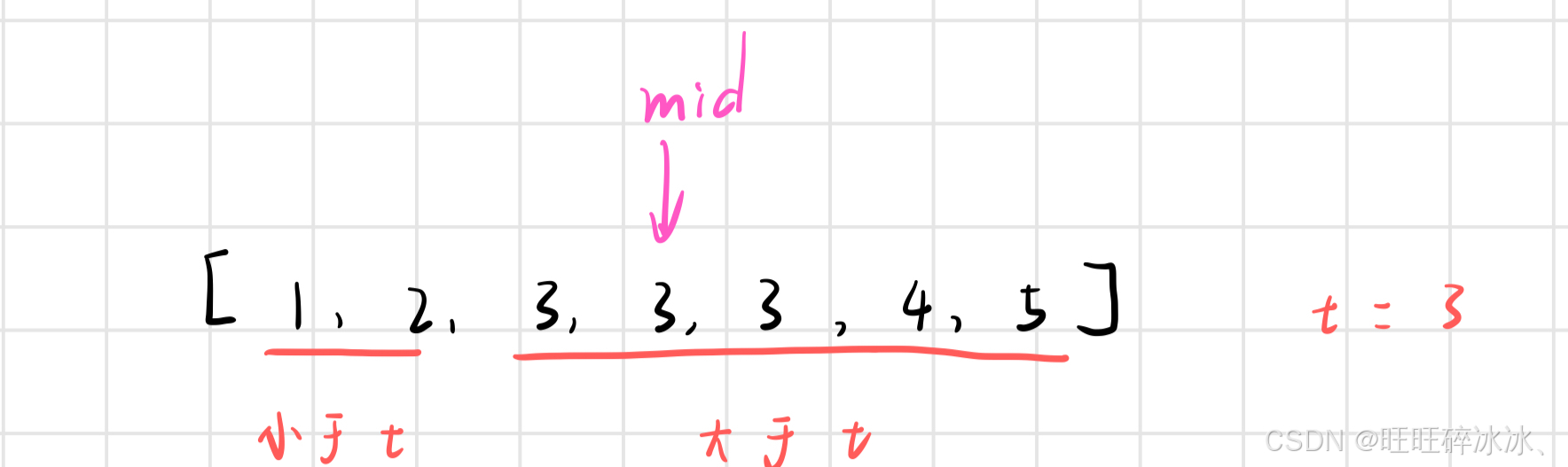
   如果 x >= t ，上一篇普通的二分查找是让 right = mid - 1，如图所示，如果 mid 的位置刚好是左端点，那么 right 更新后将找不到左端点，会错过
   
   所以我们要让 right = mid ，然后在 left 与 right 中继续寻找目标值
   

问题：

• 循环条件: left < right
  普通二分的循环条件为 left <= right ，现在就让我们来分析为什么不取等号

分为三种情况

1. 有结果
   当 left = right 的时候，就是最终结果

2. 全大于 t
   如果全都大于 t ，那么 right 会一直往左移动，直到移动到与 left 相遇为止。
   因为数组中没有最终结果，我们只需判断此时相遇的位置是否等于 t

3. 全小于 t
   如果全都小于 t ，那么 left 会一直往 右 移动，直到移动到与 right 相遇为止。
   因为数组中没有最终结果，我们只需判断此时相遇的位置是否等于 t

所以，三种情况都是当 left = right 时，此时就是最终结果，所以不取等号

当我们取等号的时候，也就是 left = right 的情况，此时 left 、right、mid 都指向 ret,
求 mid ，依旧是这个值，程序将会陷入死循环。

• 求 mid :
  （1） left + (right - left) / 2
  （2）left + (right - left + 1) / 2

有两种，接下来让我们看看选哪种

我们先看第二种：到最后一步的时候，mid 指向的位置是 right 的位置，如果此时 x >= t，那么让 right = mid，会陷入死循环，所以第二种不可以

接下来让我们看第一种：到最后一步的时候， mid 指向的位置是 left 的位置
如果 x < t ，那么 left = mid + 1，此时 left = right , 找到最终结果

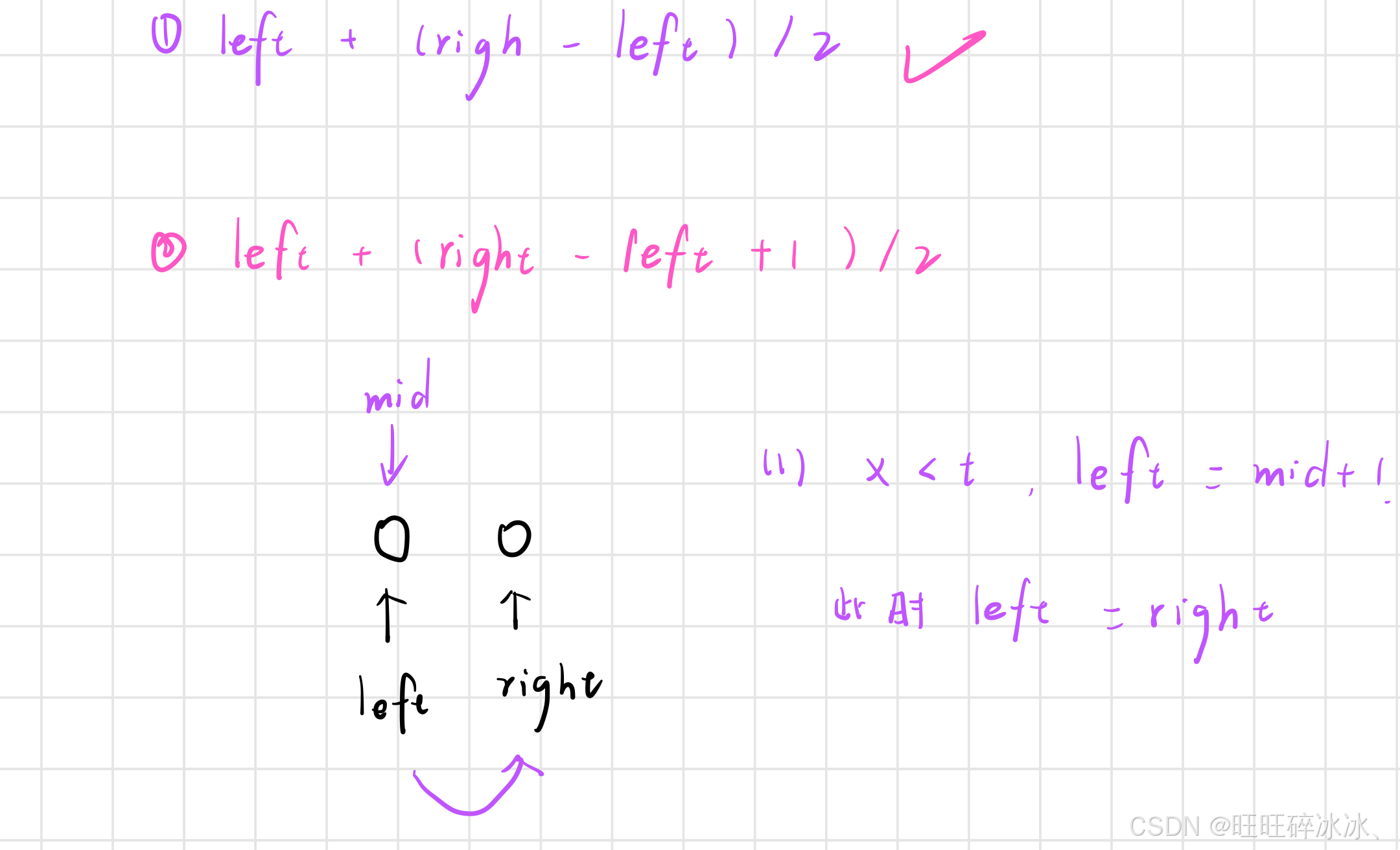
如果 x >= t，那么 right = mid ，此时 right = left ，找到最终结果

所以第一种没有问题，选择第一种

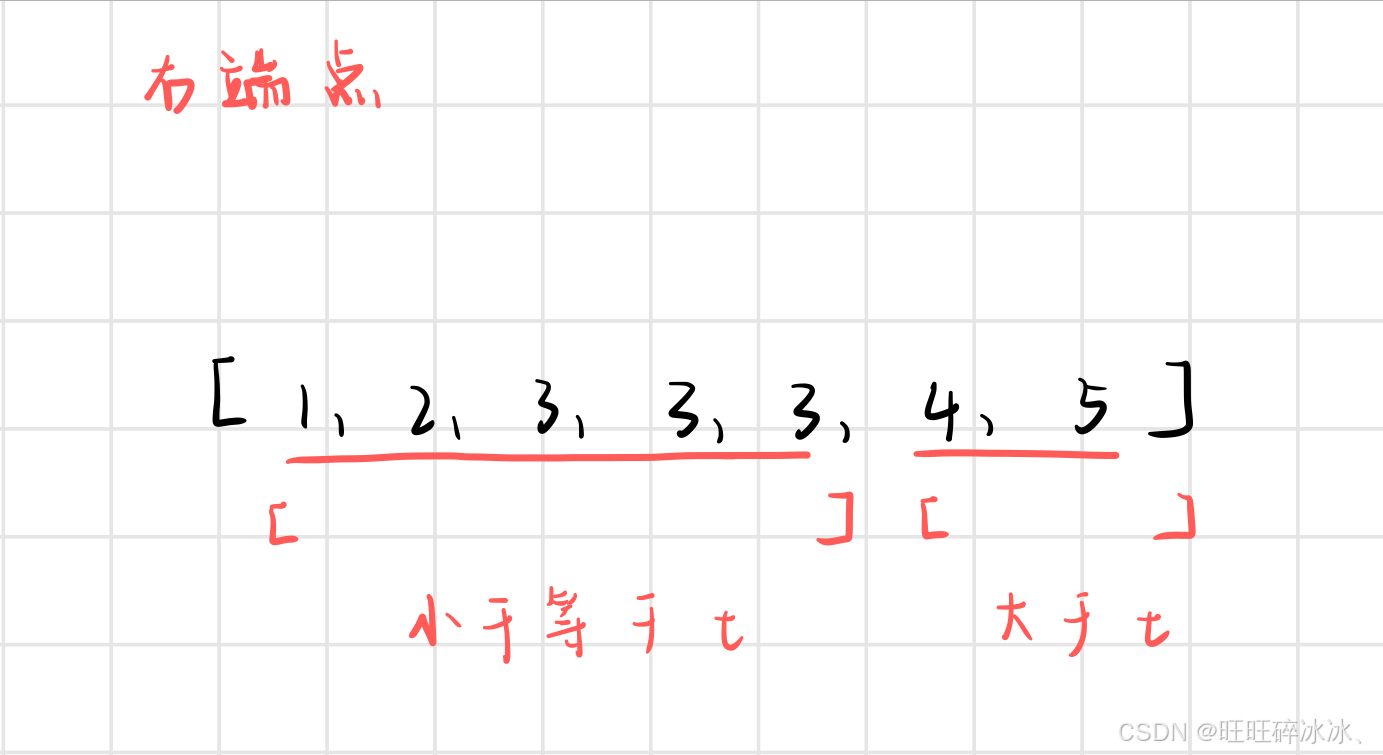
• 查找区间的右端点

找右端点，我们将目标值划分到前一个区域

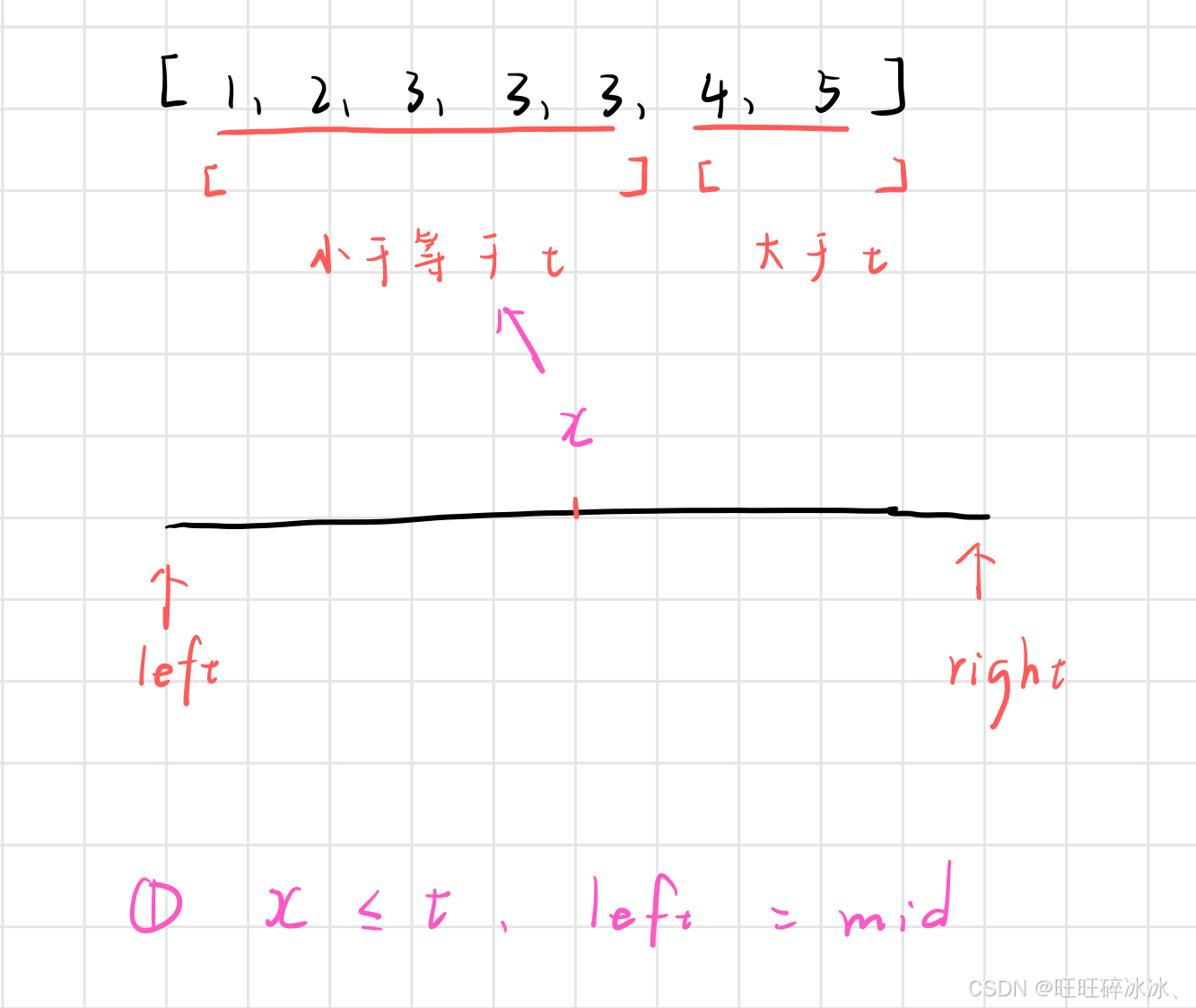
1. 如果 x <= t，此时移动 left，left = mid，继续在 left 与 right 的区间中寻找最终值
   
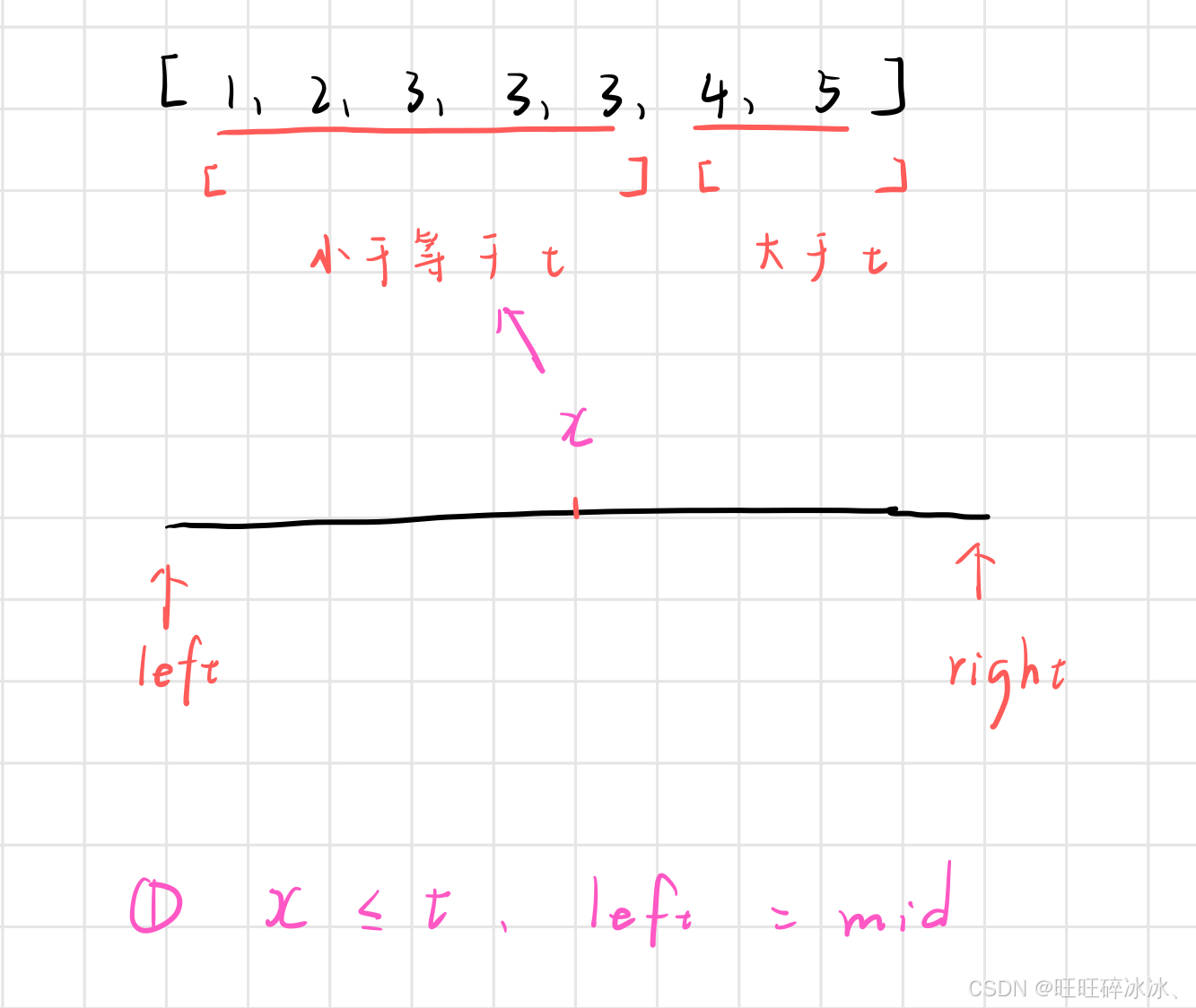
   left 不能等于 mid + 1，如果此时 mid 指向的位置就是最终值，那么 left 会跳过最终值
   

2. 如果 x > t ，此时移动 right ，right = mid - 1，继续在 left 与 right 的区间中寻找最终值
   
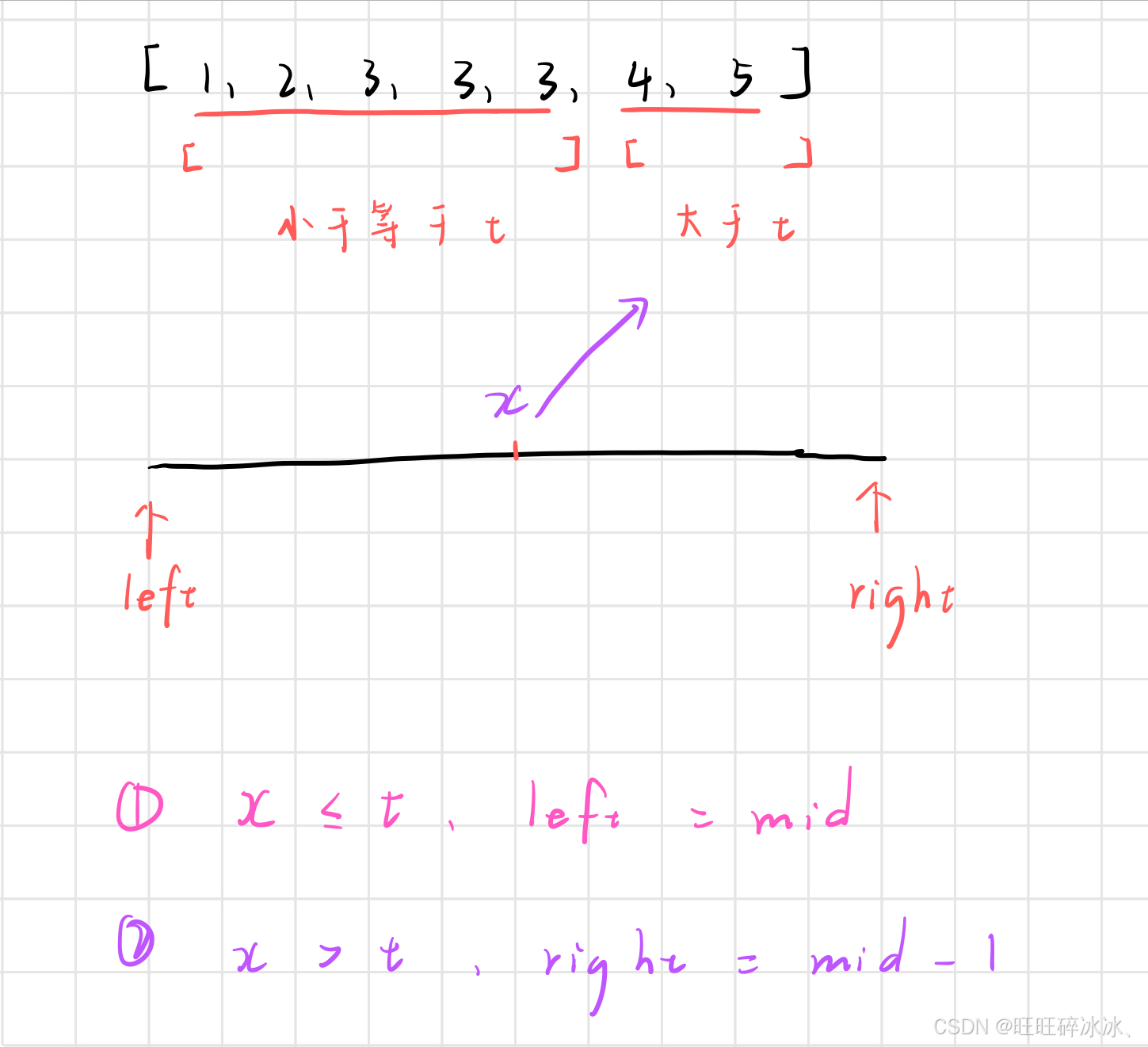
   问题：

• 循环条件：left < right，left = right 的位置就是最终结果
• 求mid
  （1） left + (right - left) / 2
  （2）left + (right - left + 1) / 2

我们先看第一种情况，到最后一步的时候，mid 此时指向 left 的位置，当 x <= t 时，left = mid，此时程序将会陷入死循环。所以第一种情况不可以。

我们再来看第二种情况，此时 mid 指向 right 的位置

当 x <= t 时，left = mid，此时left = right ，找到最终结果

当 x > t 时，right = mid - 1，此时left = right ，找到最终结果

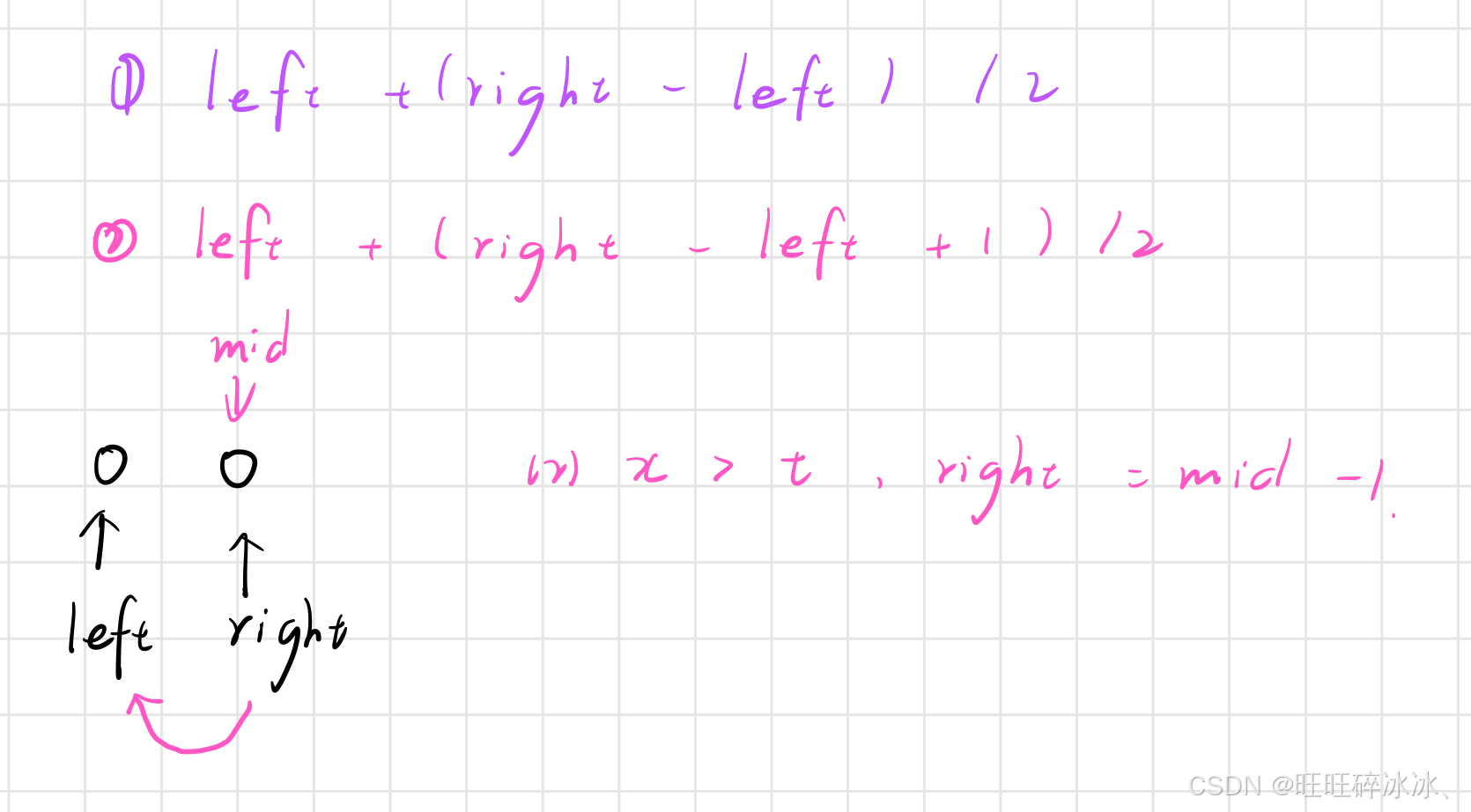
所以此时要选择第二种。

代码如下

class Solution {
    public int[] searchRange(int[] nums, int target) {
        int[] ret = new int[2];
        ret[0] = ret[1] = -1;

        //处理边界情况
        if(nums.length == 0){
            return ret;
        }

        //左端点
        int left = 0;
        int right = nums.length - 1;
        while(left < right){
            int mid = left + (right - left) / 2;
            if(nums[mid] < target){
                left = mid + 1;
            }else{
                right = mid;
            }
        }
        //此时 left = right ，用 left 或者 right 都可以
        if(nums[left] != target){
            return ret;
        }else{
            ret[0] = left;
        }

        //右端点
        left = 0;
        right = nums.length - 1;
        while(left < right){
            int mid = left + (right - left + 1) / 2;
            if(nums[mid] > target){
                right = mid - 1;
            }else{
                left = mid;
            }
        }
        ret[1] = right;
        return ret;
    }
}