运筹优化学习17：马尔科夫决策规划--例题及Matlab、Lingo和Cplex的建模实现

本文链接：https://blog.csdn.net/m1m2m3mmm/article/details/103941313

1 胡运权《运筹学》211页题目及理论分析

2 刘克《马尔科夫决策过程理论与应用》1.2节例题及代码结果

2.1 题目

2.2 例题分析

2.3 代码结果

1 胡运权《运筹学》211页题目及理论分析

1.1 题目介绍

1.2 Matlab实现

%输入参数为：决策一的状态转移矩阵和奖励矩阵；决策二的状态转移矩阵和奖励矩阵
%输出参数为：决策一的期望值与决策；决策二的期望值与决策
function [f1,d1,f2,d2] = markovOpt(P1, R1,P2,R2,N)

if N == 1
    Q1 = MatrixRowMulti(P1,R1);
    Q2 = MatrixRowMulti(P2,R2);
    [f1,d1] = max([Q1(1), Q2(1)]);
    [f2,d2] = max([Q1(2), Q2(2)]);
%     [f1,d1,f2,d2] = firstDecision(P1,R1,P2,R2);
else
    Q1 = MatrixRowMulti(P1,R1);
    Q2 = MatrixRowMulti(P2,R2);
    [ref1,~] = max([Q1(1), Q2(1)]);
    [ref2,~] = max([Q1(2), Q2(2)]);
    
    iter = 1;
    while iter ~= N
        ref = [ref1;ref2];
        tmp1 = [Q1(1,1) + P1(1,:) * ref(:,1); Q2(1,1) + P2(1,:) * ref(:,1)];
        tmp2 = [Q1(2,1) + P1(2,:) * ref(:,1); Q2(2,1) + P2(2,:) * ref(:,1)];
        [f1,d1] = max(tmp1);
        [f2,d2] = max(tmp2);
        ref1 = f1;
        ref2 = f2;
%         Q1 = [tmp1(1,1);tmp2(1,1)];
%         Q2 = [tmp1(2,1);tmp2(2,1)];
%         没搞明白此处Q为什么不用更新
        iter = iter + 1;
    end
end

end

验证代码：

%胡运权运筹学教程上的例题
P1 = [0.5,0.5; 0.4,0.6];
R1 = [9,3; 3,-7];
% Q1 = MatrixRowMulti(P1,R1)
P2 = [0.8,0.2; 0.7,0.3];
R2 = [4,4;1,-19];
% Q2 = MatrixRowMulti(P2,R2)
% %f为报酬
% [f1,d1] = max([Q1(1), Q2(1)])
% [f2,d2] = max([Q1(2), Q2(2)])
%多阶段调度的例子
[f1,d1,f2,d2] = markovOpt(P1,R1,P2,R2,1000);

值迭代算法运行打广告例子的代码运行结果
6 1 -3 1 8.2 2 -1.7 2 10.22 2 0.23 2 12.222 2 2.223 2 14.2222 2 4.2223 2 16.22222 2 6.22223 2 18.222222 2 8.222223 2 20.2222222 2 10.2222223 2 22.22222222 2 12.22222223 2 24.222222222 2 14.222222223 2

可见，工厂应该选择策略而，也就是打广告的方式才能够获得最大的总期望收益

1.3 使用Lingo求解

代码对模型的不等式做了移项处理，即将P移到不等式的左边

min = v22;
！v_ij标识阶段i处于状态j的期望奖励值
v11 >= 6; 
v12 >= -3;
- 0.5 * v11 - 0.5 * v12 + v21 >= 6;
- 0.4 * v11 - 0.6 * v12 + v22 >= -3;
- 0.8 * v11 - 0.2 * v12 + v21 >= 4;
- 0.7 * v11 - 0.3 * v12 + v22 >= -5;
- 0.5 * v21 - 0.5 * v22 + v31 >= 6;
- 0.4 * v21 - 0.6 * v22 + v32 >= -3;
- 0.8 * v21 - 0.2 * v22 + v31 >= 4;
- 0.7 * v21 - 0.3 * v22 + v32 >= -5;
- 0.5 * v31 - 0.5 * v32 + v41 >= 6;
- 0.4 * v31 - 0.6 * v32 + v42 >= -3;
- 0.8 * v31 - 0.2 * v32 + v41 >= 4;
- 0.7 * v31 - 0.3 * v32 + v42 >= -5;
!将值函数定义为自由变量
@free(v11); @free(v12);
@free(v21); @free(v22);
@free(v31); @free(v32);
@free(v41); @free(v42);

1.4 使用Cplex建模及求解

dvar float v11; dvar float v12; 
dvar float v21; dvar float v22;
dvar float v31; dvar float v32; 
dvar float v41; dvar float v42; 

minimize v41;
subject to{
v11 >= 6; 
v12 >= -3;
- 0.5 * v11 - 0.5 * v12 + v21 >= 6;
- 0.4 * v11 - 0.6 * v12 + v22 >= -3;
- 0.8 * v11 - 0.2 * v12 + v21 >= 4;
- 0.7 * v11 - 0.3 * v12 + v22 >= -5;
- 0.5 * v21 - 0.5 * v22 + v31 >= 6;
- 0.4 * v21 - 0.6 * v22 + v32 >= -3;
- 0.8 * v21 - 0.2 * v22 + v31 >= 4;
- 0.7 * v21 - 0.3 * v22 + v32 >= -5;
- 0.5 * v31 - 0.5 * v32 + v41 >= 6;
- 0.4 * v31 - 0.6 * v32 + v42 >= -3;
- 0.8 * v31 - 0.2 * v32 + v41 >= 4;
- 0.7 * v31 - 0.3 * v32 + v42 >= -5;
};

上述代码得到结果，只需更改对应的目标函数，即可得到与下表是一致的结果：

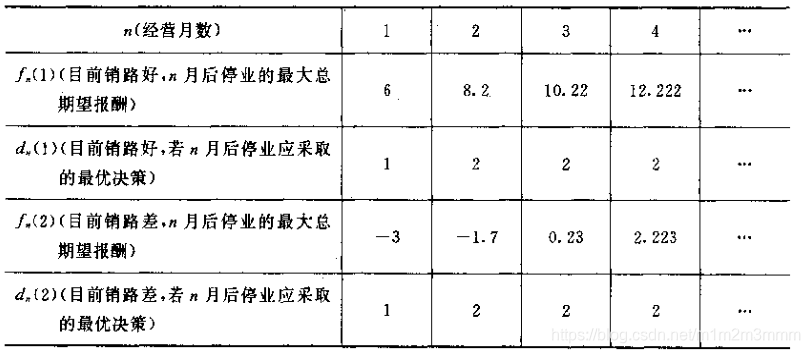
2 刘克《马尔科夫决策过程理论与应用》1.2节例题及代码结果

2.1 题目

2.2 例题分析

决策者可以做出两种决策：

决策一：采用行动a1和行动a2；对应概率矩阵和奖励，见代码中的P11和R11

决策二：采用行动a1和行动a3；对应概率矩阵和奖励，见代码中的P12和R12

2.3 代码结果

%刘克 马尔科夫决策过程理论及应用 1.2节例题1.1的求解
P11 = [0.7,0.3;0.6,0.4];
R11 = [10,10; -5, -5];
P12 = [0.7,0.3; 0.4,0.6];
R12 = [10,10; -2,-2];
iterCnt = 10;
resault = zeros(iterCnt,4);
for i = 1:iterCnt
[resault(i,1),resault(i,2),resault(i,3),resault(i,4)] = markovOpt(P11,R11,P12,R12,i);
end
resault

值迭代算法运行结果
10 1 -2 2 16.4 1 0.8 2 21.72 1 5.16 1 26.752 1 10.096 1 31.7552 1 15.0896 1 36.75552 1 20.08896 1 41.755552 1 25.088896 1 46.7555552 1 30.0888896 1 51.75555552 1 35.08888896 1 56.755555552 1 40.088888896 1

可见；决策者，应该选择决策一，即快修的方式能够在多阶段后获得最大收益。