poj 1475 Pushing Boxes(搜索)

最新推荐文章于 2022-04-29 18:31:43 发布

madaidao

最新推荐文章于 2022-04-29 18:31:43 发布

阅读量460

点赞数

分类专栏：搜索图论文章标签： acm dp 搜索 poj

本文链接：https://blog.csdn.net/madaidao/article/details/42642163

版权

图论同时被 2 个专栏收录

34 篇文章 0 订阅

订阅专栏

搜索

17 篇文章 0 订阅

订阅专栏

题目链接

Pushing Boxes

Time Limit: 2000MS		Memory Limit: 131072K
Total Submissions: 4617		Accepted: 1585		Special Judge

Description

Imagine you are standing inside a two-dimensional maze composed of square cells which may or may not be filled with rock. You can move north, south, east or west one cell at a step. These moves are called walks.
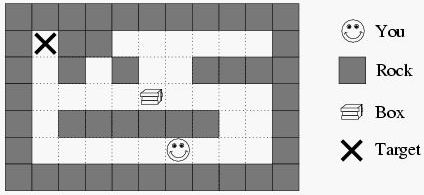
One of the empty cells contains a box which can be moved to an adjacent free cell by standing next to the box and then moving in the direction of the box. Such a move is called a push. The box cannot be moved in any other way than by pushing, which means that if you push it into a corner you can never get it out of the corner again.

One of the empty cells is marked as the target cell. Your job is to bring the box to the target cell by a sequence of walks and pushes. As the box is very heavy, you would like to minimize the number of pushes. Can you write a program that will work out the best such sequence?

Input

The input contains the descriptions of several mazes. Each maze description starts with a line containing two integers r and c (both <= 20) representing the number of rows and columns of the maze.

Following this are r lines each containing c characters. Each character describes one cell of the maze. A cell full of rock is indicated by a `#' and an empty cell is represented by a `.'. Your starting position is symbolized by `S', the starting position of the box by `B' and the target cell by `T'.

Input is terminated by two zeroes for r and c.

Output

For each maze in the input, first print the number of the maze, as shown in the sample output. Then, if it is impossible to bring the box to the target cell, print ``Impossible.''.

Otherwise, output a sequence that minimizes the number of pushes. If there is more than one such sequence, choose the one that minimizes the number of total moves (walks and pushes). If there is still more than one such sequence, any one is acceptable.

Print the sequence as a string of the characters N, S, E, W, n, s, e and w where uppercase letters stand for pushes, lowercase letters stand for walks and the different letters stand for the directions north, south, east and west.

Output a single blank line after each test case.

Sample Input

1 7
SB....T
1 7
SB..#.T
7 11
###########
#T##......#
#.#.#..####
#....B....#
#.######..#
#.....S...#
###########
8 4
....
.##.
.#..
.#..
.#.B
.##S
....
###T
0 0

Sample Output

Maze #1
EEEEE

Maze #2
Impossible.

Maze #3
eennwwWWWWeeeeeesswwwwwwwnNN

Maze #4
swwwnnnnnneeesssSSS

题意：r*c的图，已知人的初始位置和箱子的初始位置，输出一种方案使得箱子被推到目标位置，且推的次数最少。

题解：用dp[i][j][x][y]表示人的位置在（i，j），箱子的位置在（x，y）的时候最小推了多少次。转移的时候记录路径，最后输出方案即可。本质是个最短路问题，由于状态数有10^5，一个状态最多转移到8个状态，所以整个图是个稀疏图，跑堆优化的dij就可过。

代码如下：

#include<stdio.h>
#include<algorithm>
#include<queue>
#include<stack>
#include<map>
#include<set>
#include<iostream>
#include<string.h>
#include<string>
#include<math.h>
#include<stdlib.h>
#define mod 1000000007
#define inff 0x3fffffff
#define nn 30
typedef long long LL;
using namespace std;
int r,c;
string ans;
char tu[nn][nn];
int dp[nn][nn][nn][nn],tui[nn][nn][nn][nn];
int dir[4][2]={-1,0,1,0,0,-1,0,1};
bool use[nn][nn][nn][nn];
int pre[nn][nn][nn][nn];
bool xz[nn][nn][nn][nn];
struct node
{
    int px,py,bx,by;
    int walk,push;
    friend bool operator <(node a,node b)
    {
        if(a.push!=b.push)
        {
            return a.push>b.push;
        }
        else
            return a.walk>b.walk;
    }
}tem;
priority_queue<node>que;
void init()
{
    ans="";
    memset(use,false,sizeof(use));
    memset(xz,false,sizeof(xz));
    memset(pre,-1,sizeof(pre));
}
bool check(int x,int y)
{
    return x>=0&&x<r&&y>=0&&y<c;
}
void slove(int px,int py,int bx,int by)
{
    while(pre[px][py][bx][by]!=-1)
    {
        if(pre[px][py][bx][by]==0)
        {
            if(xz[px][py][bx][by])
            {
                ans+="N";
                bx-=dir[0][0],by-=dir[0][1];
            }
            else
                ans+="n";
            px-=dir[0][0],py-=dir[0][1];
        }
        else if(pre[px][py][bx][by]==1)
        {
            if(xz[px][py][bx][by])
            {
                ans+="S";
                bx-=dir[1][0],by-=dir[1][1];
            }
            else
                ans+="s";
            px-=dir[1][0],py-=dir[1][1];
        }
        else if(pre[px][py][bx][by]==2)
        {
            if(xz[px][py][bx][by])
            {
                ans+="W";
                bx-=dir[2][0],by-=dir[2][1];
            }
            else
                ans+="w";
            px-=dir[2][0],py-=dir[2][1];
        }
        else if(pre[px][py][bx][by]==3)
        {
            if(xz[px][py][bx][by])
            {
                ans+="E";
                bx-=dir[3][0],by-=dir[3][1];
            }
            else
                ans+="e";
            px-=dir[3][0],py-=dir[3][1];
        }
    }
}
void bfs()
{
    node ix;
    int i,dx,dy,bx,by;
    while(que.size())
    {
        ix=que.top();
        que.pop();
        if(tu[ix.bx][ix.by]=='T')
        {
            slove(ix.px,ix.py,ix.bx,ix.by);
            return ;
        }
        for(i=0;i<4;i++)
        {
            dx=ix.px+dir[i][0],dy=ix.py+dir[i][1];
            if(check(dx,dy)&&tu[dx][dy]!='#')
            {
                if(dx==ix.bx&&dy==ix.by)
                {
                    bx=ix.bx+dir[i][0],by=ix.by+dir[i][1];
                    if(check(bx,by)&&tu[bx][by]!='#')
                    {
                        if(!use[dx][dy][bx][by])
                        {
                            use[dx][dy][bx][by]=true;
                            tem.bx=bx,tem.by=by,tem.px=dx,tem.py=dy;
                            tem.push=ix.push+1,tem.walk=tem.walk+1;
                            que.push(tem);
                            pre[dx][dy][bx][by]=i;
                            xz[dx][dy][bx][by]=true;
                        }
                    }
                }
                else
                {
                    bx=ix.bx,by=ix.by;
                    if(!use[dx][dy][bx][by])
                    {
                        use[dx][dy][bx][by]=true;
                        tem.px=dx,tem.py=dy,tem.bx=bx,tem.by=by;
                        tem.push=ix.push,tem.walk=ix.walk+1;
                        que.push(tem);
                        pre[dx][dy][bx][by]=i;
                    }
                }
            }
        }
    }
}
int main()
{
    int i,j;
    int bx,by,sx,sy;
    int t=0;
    while(cin>>r>>c)
    {
        if(r==0&&c==0)
            break;
        t++;
        init();
        for(i=0;i<r;i++)
        {
            scanf("%s",tu[i]);
            for(j=0;j<c;j++)
            {
                if(tu[i][j]=='S')
                {
                    sx=i,sy=j;
                }
                else if(tu[i][j]=='B')
                {
                    bx=i,by=j;
                }
            }
        }
        while(que.size())
            que.pop();
        tem.px=sx,tem.py=sy,tem.bx=bx,tem.by=by;
        tem.push=0,tem.walk=0;
        que.push(tem);
        use[sx][sy][bx][by]=true;
        bfs();
        printf("Maze #%d\n",t);
        if(ans.size()==0)
            puts("Impossible.");
        else
        {
            int ls=ans.size();
            for(i=ls-1;i>=0;i--)
                cout<<ans[i];
            puts("");
        }
        puts("");
    }
    return 0;
}
/*
10 10
........##
....S..###
.#####.###
.#####.B.#
.#####.#.#
.......#.#
.#####.#.#
.....#.#.#
.##......#
T##......#
20 20
....................
....................
....................
....................
....................
....................
....................
...................T
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
.SB.................
....................
*/