Java计算长方体、四棱锥的表面积和体积

计算长方体、四棱锥的表面积和体积

Time Limit: 1000 ms Memory Limit: 65536 KiB

Problem Description

计算如下立体图形的表面积和体积。

            

                         

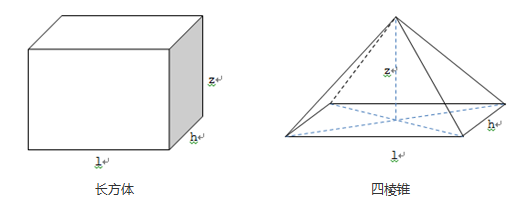
从图中观察，可抽取其共同属性到父类Rect中：长度：l  宽度：h  高度：z

在父类Rect中，定义求底面周长的方法length( )和底面积的方法area( )。

 

定义父类Rect的子类立方体类Cubic，计算立方体的表面积和体积。其中表面积area( )重写父类的方法。

定义父类Rect的子类四棱锥类Pyramid，计算四棱锥的表面积和体积。其中表面积area( )重写父类的方法。

输入立体图形的长(l)、宽(h)、高(z)数据，分别输出长方体的表面积、体积、四棱锥的表面积和体积。

Input

 输入多行数值型数据（double）；

每行三个数值，分别表示l h z

若输入数据中有非正数，则不表示任何图形，表面积和体积均为0。

Output

 行数与输入相对应，数值为长方体表面积 长方体体积 四棱锥表面积 四棱锥体积（中间有一个空格作为间隔，数值保留两位小数）

Sample Input

1 2 3
0 2 3
-1 2 3
3 4 5

Sample Output

22.00 6.00 11.25 2.00
0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00
94.00 60.00 49.04 20.00

Hint

 四棱锥体公式：V=1/3Sh，S——底面积 h——高

Source

zhouxq    

class Rect {
   double l;//长
   double h;//宽
   double z;//高
   Rect(double l, double h, double z){
	   this.l = l;
	   this.h= h;
	   this.z = z;
   }
   double length() {
	   return 2*(l+h);
   }
   double area() {
	   return l*h;
   }
}
class Cubic extends Rect{
    Cubic(double l, double h, double z){
    	super(l, h, z);
    }
	double area() {
    	double x, y, j;
    	x = l * h;
    	y = z * h;
    	j = l * z;
    	return (x+y+j)*2;
    }
	double v() {
		return l * h * z;
	}
}
 class Pyramid extends Rect{
	Pyramid(double l, double h, double z){
	    	super(l, h, z);
	    }
	double area() {
    	double sum = l * h;
    	double x, y;
    	x = Math.sqrt(z*z + (h/2)*(h/2));
    	y = Math.sqrt(z*z + (l/2) *(l/2));
    	sum += x * l + y * h;
    	return sum;
    }
	double v() {
		return (l * h * z)/3;
	}
}
import java.util.Scanner;
public class Main {

	public static void main(String[] args) {
		Scanner input = new Scanner(System.in);
		double l, h, z;
		double v, area;
		while(input.hasNext()) {
			l = input.nextDouble();
			h = input.nextDouble();
			z = input.nextDouble();
			if(l <= 0 || h <= 0 ||z <= 0) {
				System.out.println("0.00 0.00 0.00 0.00");
			}
			else {
				Cubic cu = new Cubic(l, h, z);
				v = cu.v();
				area = cu.area();
				System.out.printf("%.2f %.2f ",area, v);
				Pyramid py = new Pyramid(l, h, z);
				v = py.v();
				area = py.area();
				System.out.printf("%.2f %.2f",area, v);
				System.out.println();
			}
		}
        
	}

} 

提交时要把public类和import放在前面

计算四棱锥侧面积时三角形的高不同