1.回归案例分析
Step1:找模型

x为进化前cp值,y为进化后的cp值
Step2:方法的好处


x轴为cp值,y轴为进化后cp值

loss function是在衡量w和b的好坏
为真正的数值,
为预测值,相减的平方为估测的误差

越红代表数值越大,越偏蓝色代表结果越好,颜色代表误差大小,每个点代表一个结果

argminf(x)为取使得y最小的x

随机选取初始值w0
计算w=w0时的微分

常数项为learning rate
微分是负数要增加w值,是正数要减少w值

T次更新值后达到极小值local optimal

通过微分找极小值


在线性回归中,损失函数L是凸的。没有局部最优


e代表蓝点到红线的竖直距离
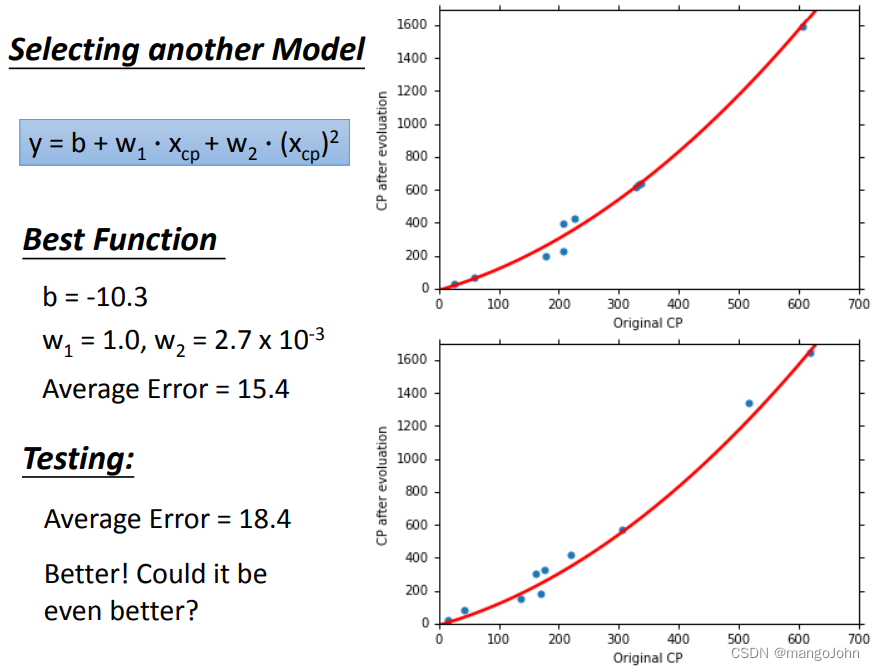
将线性改为二次函数

引入三次方
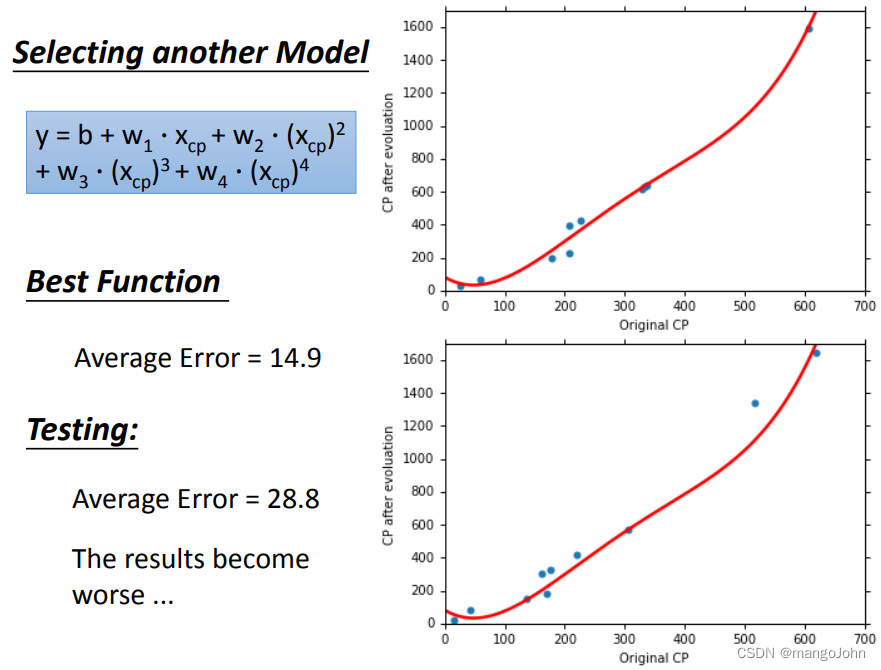 引入四次方 ,测试数据变糟糕了,过拟合
引入四次方 ,测试数据变糟糕了,过拟合

五次方,也过拟合

训练数据,avarage error变小
测试数据,avarage error变大
 这就是过拟合,模型不是越复杂越好,选合适的就行
这就是过拟合,模型不是越复杂越好,选合适的就行
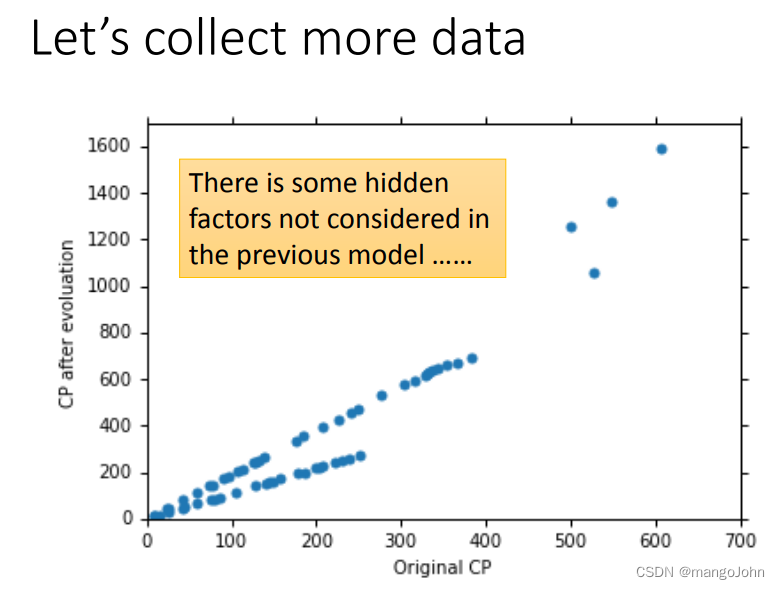


不同特征的x,选择不同的y函数代入

线性函数
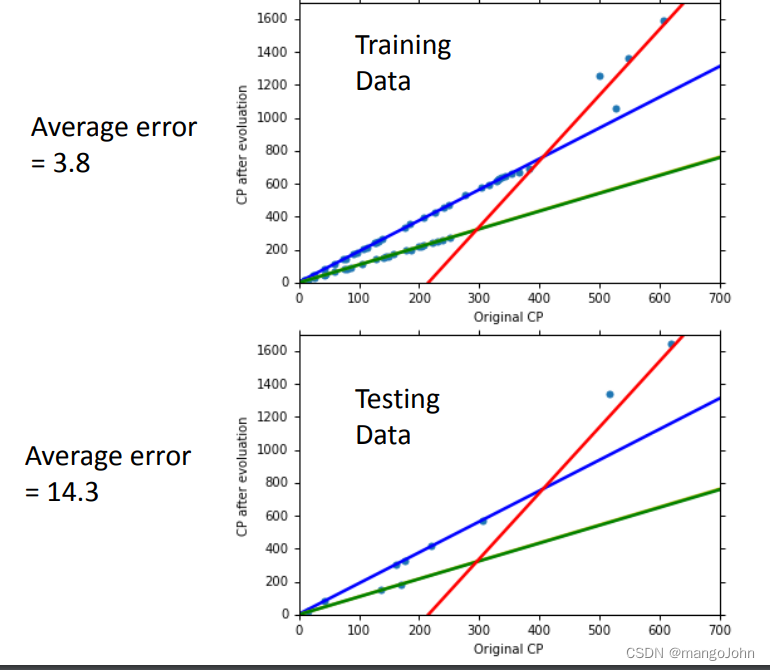 将不同特征的x都考虑到得到好的trainingdata,得到好的预测结果testingdata
将不同特征的x都考虑到得到好的trainingdata,得到好的预测结果testingdata

有没有隐藏因素
 重新设计模型
重新设计模型

为什么首选平滑函数?
如果一些噪音破坏了输入X;当测试时,一个更平滑的函数的影响更小。

训练误差:越大,考虑的训练误差越小
我们喜欢平滑的函数,但不要太平滑。

宠物小精灵:原始CP和物种几乎决定了进化后的CP 进化后(可能还有其他隐藏因素)
梯度下降法
讲座内容:理论与技巧
过度拟合和正则化
后续讲座:这些背后的更多理论
我们最终在测试数据上得到平均误差=11.1
另一组新数据如何?低估?高估了?
后续讲座:验证

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








