bzoj 4034 [HAOI2015]T2

Description

有一棵点数为 N 的树，以点 1 为根，且树点有边权。然后有 M 个

操作，分为三种：
操作 1 ：把某个节点 x 的点权增加 a 。
操作 2 ：把某个节点 x 为根的子树中所有点的点权都增加 a 。
操作 3 ：询问某个节点 x 到根的路径中所有点的点权和。
Input

第一行包含两个整数 N, M 。表示点数和操作数。

接下来一行 N 个整数，表示树中节点的初始权值。
接下来 N-1 行每行三个正整数 fr, to ， 表示该树中存在一条边 (fr, to) 。
再接下来 M 行，每行分别表示一次操作。其中第一个数表示该操
作的种类（ 1-3 ） ，之后接这个操作的参数（ x 或者 x a ） 。
Output

对于每个询问操作，输出该询问的答案。答案之间用换行隔开。

Sample Input

5 5

1 2 3 4 5

1 2

1 4

2 3

2 5

3 3

1 2 1

3 5

2 1 2

3 3
Sample Output

6

9

13

嘿 看这种题想法：
哦树剖+线段树

/再见

好吧 然后 dfs序研究了一会 发现 树状数组 貌似可以

然后第一个第三个好说

第二个怎么办？

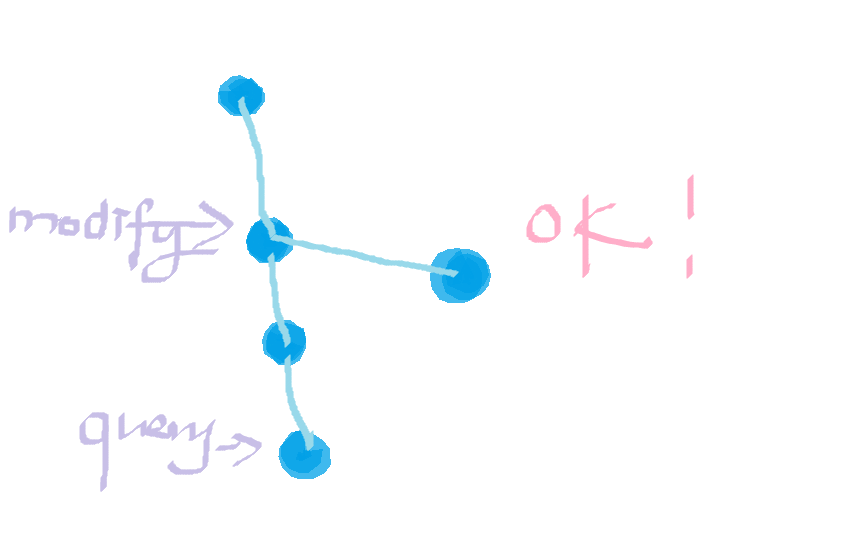
然后我们发现 只考虑第二个操作 一个点x到根节点的值为
deep位深度，w[i]为 某次第二次操作增加的 值
(deep[x]+1)*sum(w[i)
但是这样是多的。你把 他的干接点之前的也算上了
那就再减去多加的Σ (deep[root[x]])*w[i] 就搞定了
so
三个树状数组 搞定 二维还是结构体随你啦~~

#include<cstdio>
#include<cstring>
#include<algorithm>
#define int long long
using namespace std;
//by mars_ch
long long c[1000005][5];
int in[100005],out[100005],v[100005],dis[100005],time;
int n,m;
struct data
{
    int f,t,w,nxt;
 } e[1000005*2];
 int first[100005],tot;
void add(int a,int b)
{
    e[tot].f=a,e[tot].t=b;
    e[tot].nxt=first[a];
    first[a]=tot++;
}
void dfs(int x,int fa)
{
    in[x]=++time;
    for(int i=first[x];i!=-1;i=e[i].nxt)
    {
        int t=e[i].t;
        if(t == fa) continue;
        dis[t]=dis[x]+1;
        dfs(t,x);
    }
    out[x]=++time;
}
int lowbit(int x)
{
    return x&(-x);
}
void updata(int a,int b,int t)
{
    while(a<=time)
    {
        c[a][t]+=b;
        a+=lowbit(a);
    }
}
long long query(int a,int t)
{
    long long res=0;
    while(a)
    {
        res+=c[a][t];
        a-=lowbit(a);
    }
    return res;
}
signed main()
{
    scanf("%lld%lld",&n,&m);
    memset(first,-1,sizeof(first));
    for(int i=1;i<=n;i++)
    {
        scanf("%lld",&v[i]);
    }
    for(int i=1;i<=n-1;i++)
    {
        int a,b;
        scanf("%lld%lld",&a,&b);
        add(a,b);
        add(b,a);
    }
    dfs(1,0);
    for(int i=1;i<=n;i++)
    {
        updata(in[i],v[i],0);
        updata(out[i],-v[i],0);
    }
    for(int i=1;i<=m;i++)
    {
        int op;
        scanf("%lld",&op);
        if(op == 1)
        {
            int x,y; 
            scanf("%lld%lld",&x,&y);
            updata(in[x],y,0);
            updata(out[x],-y,0);
        }
        if(op == 2)
        {
            int x,y;
            scanf("%lld%lld",&x,&y);
            updata(in[x],y,1);
            updata(out[x],-y,1);
            updata(in[x],1ll*dis[x]*y,2);
            updata(out[x],-1ll*dis[x]*y,2);
        }
        if(op == 3)
        {
            int x;
            scanf("%lld",&x);
            long long ans=query(in[x],0)+query(in[x],1)*1ll*(dis[x]+1)-query(in[x],2);
            printf("%lld\n",ans);
        }
    }
    return 0;
}