本节介绍特征多项式和特征值与特征向量的计算
1 特征多项式
nxn矩阵A的特征多项式:
det(A - aI) 记做pa
2 求特征值与特征向量
对于方程det(A - aI) = 0 方程的根就是A的特征值,最后将特征值带入公式(A-aI)h=0中解出特征向量。
下边是两个例子:
(i) 例一
该方程有两个根:
他们就是特征值 带入求得对应的特征向量:
(ii)例二 利用特征值和特征向量求斐波那契公式的通项公式:
斐波那契数列的递推式:
数列的前10项:
0,1,1,2,3,5,8,13,21,34
用矩阵和向量重写递推式:
通过递推得到:
列出特征多项式的方程:
求解特征值如下:
对应的特征向量满足:
令特征向量第一个分量为1得:
将初始向量表示为特征向量的线性组合:
带入上边的递推式有:
由于数列都为整数:








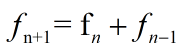
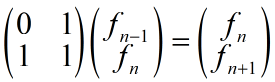
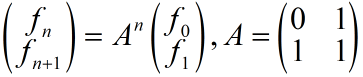
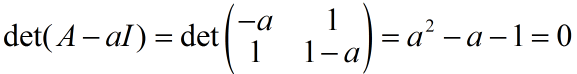
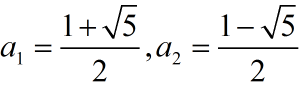
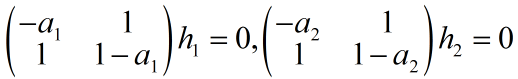
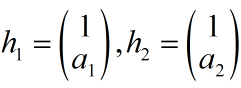
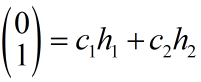
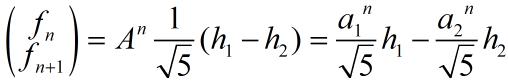
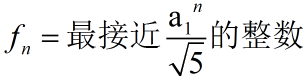

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








