cf 1012B Chemical table

一 原题

D. Chemical table

time limit per test: 1 second

memory limit per test: 512 megabytes

input: standard input

output: standard output

Innopolis University scientists continue to investigate the periodic table. There are n·m known elements and they form a periodic table: a rectangle with n rows and m columns. Each element can be described by its coordinates (r, c) (1 ≤ r ≤ n, 1 ≤ c ≤ m) in the table.

Recently scientists discovered that for every four different elements in this table that form a rectangle with sides parallel to the sides of the table, if they have samples of three of the four elements, they can produce a sample of the fourth element using nuclear fusion. So if we have elements in positions (r1, c1), (r1, c2), (r2, c1), where r1 ≠ r2 and c1 ≠ c2, then we can produce element (r2, c2).

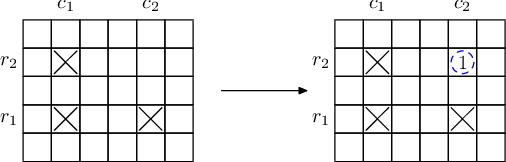
Samples used in fusion are not wasted and can be used again in future fusions. Newly crafted elements also can be used in future fusions.

Innopolis University scientists already have samples of q elements. They want to obtain samples of all n·m elements. To achieve that, they will purchase some samples from other laboratories and then produce all remaining elements using an arbitrary number of nuclear fusions in some order. Help them to find the minimal number of elements they need to purchase.

Input

The first line contains three integers n, m, q (1 ≤ n, m ≤ 200 000; 0 ≤ q ≤ min(n·m, 200 000)), the chemical table dimensions and the number of elements scientists already have.

The following q lines contain two integers ri, ci (1 ≤ ri ≤ n, 1 ≤ ci ≤ m), each describes an element that scientists already have. All elements in the input are different.

Output

Print the minimal number of elements to be purchased.

Examples

input

Copy

2 2 3
1 2
2 2
2 1

output

Copy

0

input

Copy

1 5 3
1 3
1 1
1 5

output

Copy

2

input

Copy

4 3 6
1 2
1 3
2 2
2 3
3 1
3 3

output

Copy

1

Note

For each example you have a picture which illustrates it.

The first picture for each example describes the initial set of element samples available. Black crosses represent elements available in the lab initially.

The second picture describes how remaining samples can be obtained. Red dashed circles denote elements that should be purchased from other labs (the optimal solution should minimize the number of red circles). Blue dashed circles are elements that can be produced with nuclear fusion. They are numbered in order in which they can be produced.

Test 1

We can use nuclear fusion and get the element from three other samples, so we don't need to purchase anything.

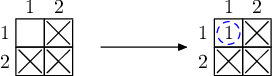
Test 2

We cannot use any nuclear fusion at all as there is only one row, so we have to purchase all missing elements.

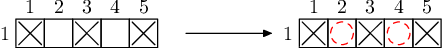
Test 3

There are several possible solutions. One of them is illustrated below.

Note that after purchasing one element marked as red it's still not possible to immidiately produce the middle element in the bottom row (marked as 4). So we produce the element in the left-top corner first (marked as 1), and then use it in future fusions.

 

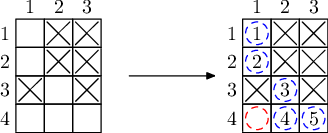
二 分析

给你一个n*m的矩形，一开始有q个格子上被标记。对于任意两行两列，如果交汇的四个格子中有三个被标记，那么第4个会被自动标记。问你至少需要手动标记几个格子，使得整个矩形内的格子都被标记。

分析：构造一个有(n+m)个点的图，如果格子(r, c)一开始被标记，就连一条从点r到点c+n的边。统计一下图中连通分量的个数即可

 

三 代码

/*
 * AUTHOR: maxkibble
 * LANG: C++
 * PROB: 1012B
 * */

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

#define pb push_back

const int maxn = 4e5 + 5;

int n, m, q, ans;
bool v[maxn];
vector<int> g[maxn];

void dfs(int x) {
    if (v[x]) return;
    v[x] = true;
    for (int y: g[x]) dfs(y);
}

int main() {
    ios::sync_with_stdio(false);
    cin >> n >> m >> q;
    int x, y;
    while (q--) {
        cin >> x >> y; y += n;
        g[x].pb(y); g[y].pb(x);
    }
    for (int i = 1; i <= n + m; i++)
        if (!v[i]) {
            dfs(i);
            ans++;
        }
    cout <<  ans - 1 << endl; 
    return 0;
}

DSU求连通分量：

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

#define pb push_back

const int maxn = 4e5 + 5;

int n, m, q, ans;

struct DSU {
    int num;
    int fa[maxn];

    void init(int t) {
        num = t;
        for (int i = 1; i <= num; i++) fa[i] = i;
    }

    int getRoot(int x) {
        if (fa[x] == x) return x;
        return fa[x] = getRoot(fa[x]);
    }

    void merge(int x, int y) {
        fa[getRoot(y)] = fa[getRoot(x)];
    }
} dsu;

int main() {
    ios::sync_with_stdio(false);
    cin >> n >> m >> q;
    dsu.init(n + m);
    int x, y;
    while (q--) {
        cin >> x >> y; y += n;
        dsu.merge(x, y);
    }
    for (int i = 1; i <= n + m; i++) if (dsu.fa[i] == i) ans++;
    cout <<  ans - 1 << endl; 
    return 0;
}