变分推断一（基于平均场理论求解Q）_平均场定理变分推断-CSDN博客

本文链接：https://blog.csdn.net/mch2869253130/article/details/102812013

本文主要参考B站的白板推导系列，推荐大家观看。

什么是变分推断

变分推断是贝叶斯学习中常用到的，含有隐变量模型的学习推理方法。变分推断和马尔可夫链蒙特卡洛法（MCMC）属于不同的技巧。MCMC通过随机抽样的方法近似的计算模型的后验概率，其背后的数学支撑是大数定理，采样的次数越多，越逼近与真实的后验概率。变分推断则通过解析的方法计算模型的后验概率的近似值。

$X$ ：观测变量
$Z$ ：latent variable + parameter
在变分推断中，样本点 $X$ 被称为观测变量（observed data），未知参数和潜变量被称为不可观测变量，都用 $Z$ 来表示。

机器学习的模型的参数的求解通常有3中方法，最大似然估计，最大后验估计和贝叶斯估计，在最大后验估计和贝叶斯估计方法中要根据观测数据来求 $Z$ 的后验分布，也就是求 $P (Z ∣ X)$ ，但是有的时候， $P (Z ∣ X)$ 是不好求的，所以尝试用一个容易求解的分布 $Q$ 来逼近 $P (Z ∣ X)$ ，当 $Q$ 和 $P (Z ∣ X)$ 之前的差距很小时就可以用 $Q$ 来近似代替 $P (Z ∣ X)$ 。之后就可以使用最大后验估计或贝叶斯估计的方法求解参数。

变分推断的数学原理

根据概率公式，我们有
$\tag{1} logP(X) = logP(X, Z) - logP(Z|X)$
(1)式右边的两项log里面的部分同时除以 $Q (Z)$ ，（1）式的值依然相等。即
$\tag{2} logP(X) = log{P(X, Z) \over Q(Z)} - log{P(Z|X) \over Q(Z)}$
(2)式两边同时乘以 $Q (Z)$ ，并对 $Z$ 求积分得。

$\begin{aligned} 左边 = & \int_{Z} logP(X)Q(Z)dZ \\ & = logP(X) \\ 右边= & \int_{Z} ( Q(Z)log{P(X, Z) \over Q(Z)}- Q(Z)log{P(Z|X) \over Q(Z)})dZ \\ = & \int_{Z} Q(Z)log{P(X, Z) \over Q(Z)}dZ - \int_{Z} Q(Z)log{P(Z|X) \over Q(Z)})dZ \\ = & L(Q) + KL(Q||P) \end{aligned}$
上式中，第一项记为 $L (Q)$ ，第二项连同负号是KL散度的形式，表示的是后验分布 $P (Z ∣ X)$ 与分布 $Q (Z)$ 之间的距离。
所以有
$\begin{aligned} \tag{3} logP(X) = L(Q) + KL(Q||P) \end{aligned}$
$L (Q)$ 也可以写成 $L(Q)= E_{Q}[logP(X,Z)-logQ(Z)]$

由于 $K L (Q ∣ ∣ P)$ 是大于等于0的，所以 $L (Q) < = l o g P (X)$ ，此时也称 $L (Q)$ 是ELBO（证据下界）。值得注意的是，此时的 $L (Q)$ 是分布 $Q$ 的函数（也称为泛函），当数据给定的时候， $l o g P (X)$ 是不变的，所以如果我们让 $L (Q)$ 最大化，也就是会让 $K L (Q ∣ ∣ P)$ 最小化，那么我们就会找到一个 $Q$ ，从而用这个 $Q$ 近似后验分布 $P (Z ∣ X)$ ，此时这个分布 $Q$ 就称作变分分布。

变分分布Q的求解

平均场理论假设 $Q (Z)$ 对于 $Z$ 的所有分量都是条件独立于参数的（假设 $Z$ 有 $M$ 个分量），也就是
$\tag{4} Q(Z) = \prod_{i}^{M} Q_{i}(Z_{i})$
由前面的推导知，
$\tag{5} L(Q) = \int_{Z} Q(Z)log{P(X, Z) \over Q(Z)}dZ$
将（4）代入（5）式，得
$\begin{aligned} \tag{6} L(Q) = \int_{Z} \prod_{i}^{M}Q_{i}(Z_{i})logP(X,Z) dZ-\int_{Z} \prod_{i}^{M}Q_{i}(Z_{i})log\prod_{i}^{M}Q_{i}(Z_{i})dZ \\ = \int_{Z} \prod_{i}^{M}Q_{i}(Z_{i})logP(X,Z) dZ - \int_{Z} \prod_{i}^{M}Q_{i}(Z_{i})\sum_{i}^{M} logQ_{i}(Z_{i})dZ \end{aligned}$
考虑其中的某一项 $Q_{j}(Z_{j})$ ，分别计算(6)式的两部分。
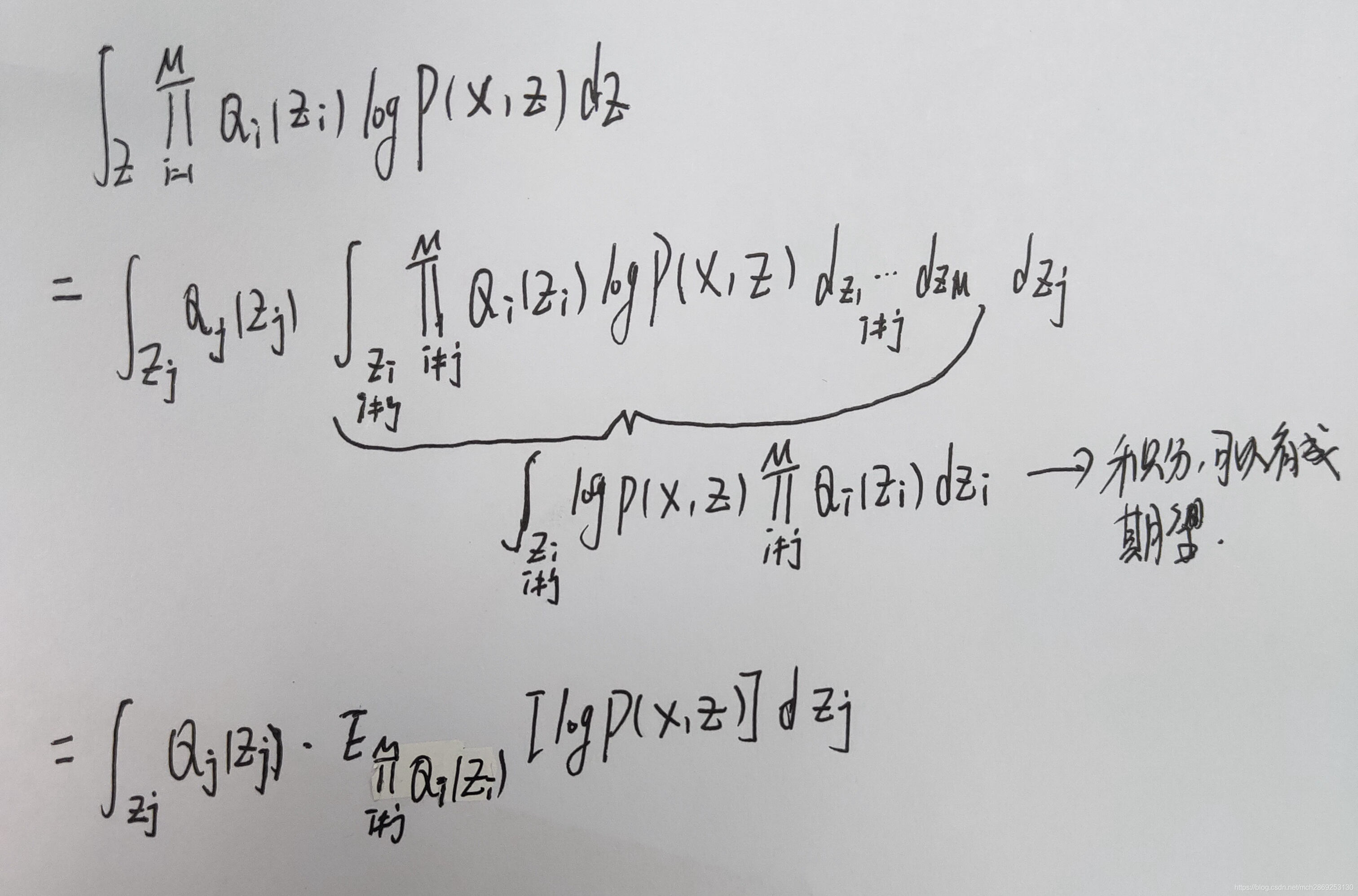
在这里插入图片描述

得到 $Q_{i}(Z_{i})$ 之后，根据公式（4）便得到了我们要求的分布 $Q$ 。

变分推断与EM算法的关系

在EM算法总结一文中，详细阐述了EM算法的推导，我们发现，EM算法推导的ELBO的形式和变分推断的ELBO完全相同。即
$\tag{7} ELBO = \int_Zq(Z)log{p(X,Z) \over q(Z)}dZ =E_{q}[logp(X,Z)]-E_{q}[logq(Z)]$
在（7）式的期望一项中，第一项是 $(X, Z)$ 的联合概率分布的对数似然，第二项是新引入的分布 $q (Z)$ 的对数似然。

EM算法和变分推断的区别在于对分布 $q (Z)$ 的计算方式不同。EM算法假设 $q (Z) = p (Z ∣ X)$ 且 $p (Z ∣ X)$ 容易计算处来，通常用贝叶斯公式 $\over \int_Zp(Z)p(X|Z)dZ}$ 就可以算出。而变分推断则考虑更一般情况，使用平均场理论来计算 $q(Z)=\prod_{i=1}^{m}q_{i}(Z_i)$ ，也就是（4）式来计算。当模型复杂时，EM算法未必可用，但变分推断仍然可用。

其它部分与EM算法一样，也分为E步和M步，通过优化似然函数的紧下界来求解参数。区别就是上面提到的，在E步没有直接计算隐变量的后验，而是用一个近似分布 $q (Z)$ 去逼近 $p (Z ∣ X)$ ，这个 $q (Z)$ 是由你自己去定义的。

下面总结变分推断算法框架：

随机初始化未知参数，初始化值记为 $\theta^{old}$
E-STEP:
- 求隐变量 $Z$ 的后验的近似分布 $q (Z)$ ： $q(Z)=\prod_{i=1}^mq_{i}(Z_i)$
- 求ELBO： $=E_{q}[logp(X,Z|\theta^{old})]-E_{q}[logq(Z)]$
- 根据ELBO对 $q (Z)$ 最大化，也就是 $\hat{q(Z)} =argmax_{q(Z)}E_{q}[logp(X,Z|\theta^{old})]-E_{q}[logq(Z)]$ ，令 $q(Z)=\hat{q(Z)}$
M-STEP:
根据 $E_{q}[logp(X,Z|\theta)]-E_{q}[log\hat{q(Z)}]$ 对 $\theta$ 最大化，也就是 $\hat{\theta}=argmax_{\theta} E_{q}[logp(X,Z|\theta)]-E_{q}[log\hat{q(Z)}]$
令 $\theta^{old} = \hat{\theta}$ ，并开启下一轮迭代。