假设变分后验为高斯分布,变分参数是 λ \lambda λ,也就是 λ = [ μ , Σ ] \lambda=[\mu, \Sigma] λ=[μ,Σ],输入为 x x x,这里的 x x x表示一个样本。注意,每个样本都有与之对应的变分参数,也就是样本集 X = [ x ( 1 ) , x ( 2 ) , . . . , x ( N ) ] X=[x^{(1)}, x^{(2)},..., x^{(N)}] X=[x(1),x(2),...,x(N)],变分参数集 Λ = [ λ ( 1 ) , λ ( 2 ) , . . . , λ ( N ) ] \Lambda=[\lambda^{(1)}, \lambda^{(2)}, ..., \lambda^{(N)}] Λ=[λ(1),λ(2),...,λ(N)]。
变分推理就是求解变分参数 λ \lambda λ的过程。有两种技术,第一种是Hoffman在2013年提出的stochastic variational inference(SVI),随机梯度变分推理。第二种是Kingma在2014年提出的Amortized Variational inference(AVI) ,叫做平摊变分推理。
VAE的变分推理是属于Amortized Variational inference,每个样本 x x x的变分参数都是通过同一个网络推理出的,这个网络是共享的。神经网络就相当于一个函数逼近器,所以VAE有一个约束就是认为变分参数 λ \lambda λ是输入 x x x的函数。但是这个约束太强了,可能会使得VAE的ELBO与loglikelihood之间存在一个gap,在复杂的数据集上,这个gap会显著影响VAE的性能。
SVI是另一种推理方法,SVI是特定于数据的,SVI会随机初始化 Λ \Lambda Λ,然后通过梯度的方法来最大化ELBO,然后迭代求解变分参数。也就是说,变分参数不是由网络推理出的,而是通过梯度来优化的。
可见VAE的优点就是快速,缺点是由gap太大,得到的变分参数通常是次优的。SVI优点是对每个样本都迭代执行变分推断,缺点是比VAE耗时。本文作者将二者结合起来,用VAE推理出的变分参数初始化SVI的变分参数,然后再用SVI 特定于样本微调变分参数。
Variational Inference
l
o
g
p
(
x
;
θ
)
≥
E
q
(
z
;
λ
)
[
l
o
g
p
(
x
∣
z
;
θ
)
]
−
K
L
[
q
(
z
;
λ
)
∣
∣
p
(
z
)
]
=
E
L
B
O
(
λ
,
θ
,
x
)
(1)
\begin{aligned} \tag{1} logp(x;\theta) \ge & E_{q(z;\lambda)}[logp(x|z;\theta)] - KL[q(z;\lambda)||p(z)] \\ = & ELBO(\lambda, \theta, x) \end{aligned}
logp(x;θ)≥=Eq(z;λ)[logp(x∣z;θ)]−KL[q(z;λ)∣∣p(z)]ELBO(λ,θ,x)(1)
(1)式是变分推断的ELBO,
λ
\lambda
λ是变分参数,
θ
\theta
θ是生成部分
p
(
x
∣
z
)
p(x|z)
p(x∣z)的参数。通常情况下,给定样本集
X
X
X,变分推断的任务是寻找最优的
Λ
\Lambda
Λ和生成模型参数
θ
\theta
θ,使得
∑
i
=
1
N
E
L
B
O
(
λ
(
i
)
,
θ
,
x
(
i
)
)
\sum_{i=1}^{N}ELBO(\lambda^{(i)},\theta, x^{(i)})
∑i=1NELBO(λ(i),θ,x(i))最大化。
Stochastic Variational Inference
SVI的推理过程如下:

K
K
K是迭代的次数,
α
\alpha
α是学习速率。可以看到,变分参数
λ
\lambda
λ的优化和生成模型的参数
θ
\theta
θ的优化是分开的,并不是由同一个ELBO算出的,这样
θ
\theta
θ与
λ
\lambda
λ的适应性可能不是很好。
Amortized Variational Inference
VAE使用一个全局共享的推理网络计算每个样本的变分参数,推理网络表示为
e
n
c
(
x
;
ϕ
)
enc(x;\phi)
enc(x;ϕ),表示输入为
x
x
x,网络参数是
ϕ
\phi
ϕ

与SVI相比,AVI要更新推理网络的参数
ϕ
\phi
ϕ,
λ
\lambda
λ由推理网络计算得到,并且
ϕ
\phi
ϕ与
θ
\theta
θ是由相同的ELBO算出的,这样可以
λ
与
θ
\lambda与\theta
λ与θ二者可以更好的适应。另外,AVI是在输入上进行推理,而SVI是在ELBO的迭代优化上进行推理,所以AVI更快。
Semi-Amortized Variational Autoencoders
SA-VAE在输入上利用推理网络提供初始化变分参数,然后运行SVI对其进行优化。

这里为了更新编码器(推理网络)和解码器(生成网络)的参数(分别是
ϕ
\phi
ϕ和
θ
\theta
θ),需要第
K
K
K次迭代的
E
L
B
O
(
λ
K
,
θ
,
x
)
ELBO(\lambda_{K}, \theta, x)
ELBO(λK,θ,x)的梯度能够传到
θ
\theta
θ和
ϕ
\phi
ϕ。
这里主要分析一下
E
L
B
O
(
λ
K
,
θ
,
x
)
ELBO(\lambda_{K}, \theta, x)
ELBO(λK,θ,x)的梯度如何传到
ϕ
\phi
ϕ,由于
λ
0
\lambda_{0}
λ0是由参数为
ϕ
\phi
ϕ的推理网络算出的,所以根据链式法则,
d
E
L
B
O
(
λ
K
,
θ
,
x
)
d
ϕ
=
d
E
L
B
O
(
λ
K
,
θ
,
x
)
d
λ
0
∗
d
λ
0
d
ϕ
(1)
\tag{1} {dELBO(\lambda_{K}, \theta, x) \over d\phi} = {dELBO(\lambda_{K}, \theta, x) \over d\lambda_{0}}*{d\lambda_{0} \over d\phi}
dϕdELBO(λK,θ,x)=dλ0dELBO(λK,θ,x)∗dϕdλ0(1)
那么(1)式右边的两项如何求解,先看 d λ 0 d ϕ {d\lambda_{0} \over d\phi} dϕdλ0,我们前面已经假设后验分布是高斯分布 了,那么 λ 0 = [ μ 0 , Σ 0 ] \lambda_{0}=[\mu_{0}, \Sigma_{0}] λ0=[μ0,Σ0],注意,这里的下标不是指样本的下标,而是指第几轮SVI推理。
所以 λ 0 \lambda_{0} λ0应该是两个向量,也就是向量对网络参数 ϕ \phi ϕ求导,在pytorch中,只需要在backward()中传入一个和 λ 0 \lambda_{0} λ0维度一样的向量即可。
关键是 d E L B O ( λ K , θ , x ) d λ 0 {dELBO(\lambda_{K}, \theta, x) \over d\lambda_{0}} dλ0dELBO(λK,θ,x)如何求解,如果用 E L B O ( λ K , θ , x ) . ELBO(\lambda_{K}, \theta, x). ELBO(λK,θ,x).backward方式,梯度是传不到 λ 0 \lambda_{0} λ0的,因为中间还有 E L B O ( λ K − 1 , θ , x ) , E L B O ( λ K − 2 , θ , x ) , . . . , E L B O ( λ 1 , θ , x ) ELBO(\lambda_{K-1}, \theta, x),ELBO(\lambda_{K-2}, \theta, x), ...,ELBO(\lambda_{1}, \theta, x) ELBO(λK−1,θ,x),ELBO(λK−2,θ,x),...,ELBO(λ1,θ,x),先考虑 E L B O ( λ 1 , θ , x ) ELBO(\lambda_{1}, \theta, x) ELBO(λ1,θ,x)的梯度如何传到 λ 0 \lambda_{0} λ0
用SVI得到新的变分参数
λ
1
=
λ
0
+
α
∇
λ
E
L
B
O
(
λ
0
,
θ
,
x
)
\lambda_{1}=\lambda_{0}+\alpha \nabla_{\lambda}ELBO( \lambda_{0}, \theta, x)
λ1=λ0+α∇λELBO(λ0,θ,x),令
L
=
E
L
B
O
(
λ
1
,
θ
,
x
)
L=ELBO(\lambda_{1}, \theta, x)
L=ELBO(λ1,θ,x),根据链式法则,有下式成立

上式中,
H
λ
,
λ
H_{\lambda, \lambda}
Hλ,λ表示海森矩阵,是标量对向量的二阶导数组成的矩阵,
d
L
d
λ
1
{dL \over d_{\lambda_{1}}}
dλ1dL是标量对向量的导数,是一个向量。所以上式中涉及到海森矩阵与向量的矩阵乘法,后面会提到用一种专门的算法来实现二者的乘积。
多次使用链式法则,便可求得 d E L B O ( λ K , θ , x ) d λ 0 {dELBO(\lambda_{K}, \theta, x) \over d\lambda_{0}} dλ0dELBO(λK,θ,x)。这样 E L B O ( λ K , θ , x ) ELBO(\lambda_{K}, \theta, x) ELBO(λK,θ,x)的梯度就可传到 ϕ \phi ϕ了。
所以上面的分析可以分为两个过程:
第一个过程是前向迭代
K
K
K次得到最优的变分参数
λ
K
\lambda_{K}
λK:
- λ 0 = e n c ( x ; ϕ ) \lambda_{0}=enc(x;\phi) λ0=enc(x;ϕ)
- λ k + 1 = λ k + α ∇ λ E L B O ( λ k , θ , x ) \lambda_{k+1}=\lambda_{k}+\alpha \nabla_{\lambda}ELBO( \lambda_{k}, \theta, x) λk+1=λk+α∇λELBO(λk,θ,x)
第二个过程是后向迭代 K K K次,将 L K = E L B O ( λ K , θ , x ) L_{K}=ELBO(\lambda_{K}, \theta, x) LK=ELBO(λK,θ,x)的梯度传到 λ 0 \lambda_{0} λ0:
- 通过 E L B O ( λ K , θ , x ) . b a c k w a r d ( ) ELBO(\lambda_{K}, \theta, x).backward() ELBO(λK,θ,x).backward()得到 d L K d λ K {dL_{K} \over d\lambda_{K}} dλKdLK
- d L K d λ 0 = d λ K d λ K − 1 ∗ . . . ∗ d λ 1 − λ 0 d L K d λ K {dL_{K} \over d\lambda_{0}}={d\lambda_{K} \over d\lambda_{K-1}}*...*{d\lambda_{1} \over - \lambda_{0}}{dL_{K} \over d\lambda_{K}} dλ0dLK=dλK−1dλK∗...∗−λ0dλ1dλKdLK
- 通过(1)式得到 E L B O ( λ K , θ , x ) ELBO(\lambda_{K},\theta, x) ELBO(λK,θ,x)对 ϕ \phi ϕ的梯度。
对 θ \theta θ也是同理。
最后算法框架如下图:

关于海森矩阵与向量的乘积,使用了 Hessian-vector products方法求解,并没有算二阶导。
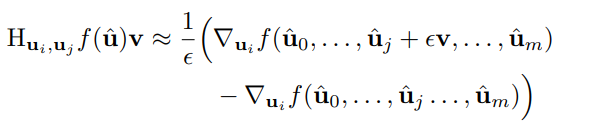











 该文探讨了变分自编码器(VAE)与随机梯度变分推断(SVI)的结合,提出了一种称为 Semi-Amortized VAE 的方法。VAE 使用共享的推理网络计算变分参数,而 SVI 则针对每个样本进行优化。SA-VAE 利用推理网络初始化 SVI 的变分参数,然后通过 SVI 进行微调,从而平衡了速度和性能。这种方法解决了 VAE 中因固定网络输出导致的次优变分参数问题,同时减少了 SVI 的计算成本。
该文探讨了变分自编码器(VAE)与随机梯度变分推断(SVI)的结合,提出了一种称为 Semi-Amortized VAE 的方法。VAE 使用共享的推理网络计算变分参数,而 SVI 则针对每个样本进行优化。SA-VAE 利用推理网络初始化 SVI 的变分参数,然后通过 SVI 进行微调,从而平衡了速度和性能。这种方法解决了 VAE 中因固定网络输出导致的次优变分参数问题,同时减少了 SVI 的计算成本。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








