二叉树（C语言）

树可以使用链表也可以用数组实现

数组的实现通过下表与树的节点的序列对应，但是该方不够灵活，而且在C语言中，数组不进行下界检查，而且不能进行动态增长。

在比较通用的实现方式使用的是树链表实现。

对于大量的数据输入，链表的线性范文时间太慢，不宜使用，树的大部分操作的运行时间平均为O(log N)

具体参照源码：

http://download.csdn.net/detail/mcu_tian/9540527

二叉树

二叉树是最简单、应用最广泛的树，通过构造表达式树，对表达式树的一些操作作为实例。

将计算表达式（只有“*”、“+”操作符，操作数用字母代替，假设输入都是合法的，不会对表达式合法性进行检查）转换为后缀表达式，通过栈的方式进行转换（参考）：

http://blog.csdn.net/mcu_tian/article/details/51493081

二叉树的节点定义如下

typedef char TreeElementType;
struct TreeNode
{
    TreeElementType element;
    struct TreeNode *right;
    struct TreeNode *left;
};
typedef struct TreeNode *nodePtr;
typedef struct TreeNode *tree;
typedef struct TreeNode node;

构建表达式树：

tree CreateExpTree(char* expStr) //输入后缀的表达式字符串，并且返回表达式树根节点指针
{
    int nstr;
    tree tmpTree;
    nodePtr tmpPtr;
    nodePtr *ptrArray;

    char ctmp;
    int ni=0;
    int i = 0;//指针数组的位置标记

    nstr = strlen(expStr);  
    ptrArray = (nodePtr *)malloc(nstr*sizeof(nodePtr));//节点指针数组
/*
 * 构建表达式树,逐字符的分析表达式字符串
 * 该表达式树的构建使用的是类似于堆得方法
 * 当字符为操作数的时候（即字母），将标记位置（i）对应的指针数组元素指向该节点，并将该节点的左右孩子节点指针设置为NULL
 * 当字符为操作符的时候（即‘+’或‘*’），将该节点的左右孩纸（left、right）设置为指针数组对应标记位置（i）的前两个元素。
 * 指针数组的标记位（i）减2，再将位置标记对应的数组元素赋值为改节点的地址
 * 在迭代遍历完成之后，返回树的根节点指针，即为节点指针数组的首元素（只有表达式输入没有问题，那么最后i一定为0）
 */
    for(;ni<nstr;++ni)  
    {
        ctmp = expStr[ni]; 
        if(islower(ctmp)||isupper(ctmp))
        {
            tmpPtr = (nodePtr)malloc(sizeof(node));
            tmpPtr->left = NULL;
            tmpPtr->right = NULL;
            tmpPtr->element = ctmp;
            ptrArray[i]=tmpPtr;
            ++i;
        }
        else
        {
            tmpPtr = (nodePtr)malloc(sizeof(node));
            tmpPtr->right = ptrArray[--i];
            tmpPtr->left = ptrArray[--i];
            tmpPtr->element = ctmp;

            ptrArray[i] = tmpPtr;
            ++i;
        }
    }
    tmpTree = ptrArray[0];
    free(ptrArray);
    return tmpTree;
}

二叉树的遍历

在构建好树之后，那么接下来就是对树进行遍历了

树的遍历有前序遍历、中序遍历、后序遍历

其中前中后对应的是根节点

前序遍历顺序为    根节点->左孩子节点->右孩子节点

中序遍历顺序为    左孩子节点->根节点->右孩子节点

后序遍历顺序为    左孩子节点->右孩子节点->根节点

树的遍历是通过递归实现的：

前序遍历：

int PreorderTraversal(tree btree,TreeElementType *result) //输入遍历树的根节点指针，然后将遍历结果输入到reuslt指向的数组中，返回遍历节点的数量
{
    static unsigned int i = 0;
    if(btree == NULL)
    {
        return i;
    }
    result[i] = btree->element;
    ++i;
    PreorderTraversal(btree->left,result);
    PreorderTraversal(btree->right,result);
    return i;
}

中序遍历：

int InorderTraversal(tree btree,TreeElementType *result)//同上
{
    static unsigned int i;
    if(btree == NULL)
    {
        return i;
    }
    InorderTraversal(btree->left,result);
    result[i] = btree->element;
    ++i;
    InorderTraversal(btree->right,result);
    return i;
}

后序遍历：二叉树的摧毁通过后序遍历，逐个进行节点的释放

int PostorderTraversal(tree btree,TreeElementType *result)//同上
{
    static unsigned int i;
    if(btree == NULL)
    {
        return i;
    }
    PostorderTraversal(btree->left,result);
    PostorderTraversal(btree->right,result);
    result[i] = btree->element;
    ++i;
    return i;
}

计算表达式为：

(a+b*c)+((d*e+f)*g)

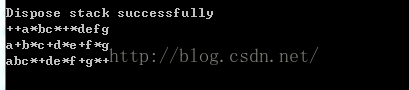
构建表达式树后，运行结果如下图（分别前序遍历、中序遍历、后序遍历）：