矢量(英语:Vector)是数学、物理学和工程科学等多个自然科学中的基本概念,指一个同时具有大小和方向的几何对象,因常常以箭头符号标示以区别于其它量而得名。直观上,矢量通常被标示为一个带箭头的线段(如右图)。线段的长度可以表示矢量的大小,而矢量的方向也就是箭头所指的方向。物理学中的位移、速度、力、动量、磁矩、电流密度等,都是矢量。与矢量概念相对的是只有大小而没有方向的标量。
在数学中,矢量也常称为向量,即有方向的量。并采用更为抽象的矢量空间(也称为线性空间)来定义,而定义具有物理意义上的大小和方向的向量概念则需要引进了范数和内积的欧几里得空间。
目录[隐藏] |
[编辑]表示方法
在文字表述时,如果已知矢量的起点和终点分别是A和B,那么这个矢量可以记为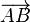 。如果是为了和其他量区别,则在符号顶上加上箭头表示矢量,如
。如果是为了和其他量区别,则在符号顶上加上箭头表示矢量,如  。
。
注:过往在排版过程中,要在字母上加上箭头比较困难,不像手写那么容易。所以在以往的书本印刷中,矢量多数会用粗体字母表示,如 ,但这样做却增加了阅读困难,因为要区分是否粗体字有时不容易,例如
,但这样做却增加了阅读困难,因为要区分是否粗体字有时不容易,例如  和
和  肉眼看很易混淆。但随着时代和技术进步,在加上电脑辅助排版,为求清楚明确起见,书籍中用粗体字母代表矢量的情况也越来越少了。
肉眼看很易混淆。但随着时代和技术进步,在加上电脑辅助排版,为求清楚明确起见,书籍中用粗体字母代表矢量的情况也越来越少了。
矢量的直观图形表示则一般使用带箭头的线段。而遇到某些特殊情况需要表示与记载纸面垂直的矢量,则会使用圆圈中打叉或打点的方式来表示(如右图)。圆圈中带点的记号(⊙)表示由纸下方指向纸上方的矢量,而圆圈中带叉的记号(⊗)则表示由纸的上方指向纸下方的矢量。由于这种记号不表示矢量的大小,所以必须时需要在旁边或其它地方另外注明。
在直角坐标系中,定义有若干个特殊的基本矢量,其它的矢量可以通过这些基本矢量来表示。在常见的三维空间直角坐标系Oxyz里,基本矢量就是以横轴(Ox)、竖轴(Oy) 以及纵轴(Oz) 为方向的三个单位矢量 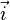 、
、 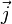 、
、 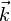 。这三个矢量取好以后,其它的矢量就可以通过三元数组来表示,因为它们可以表示成一定倍数的三个基本矢量的总合。比如说一个标示为(2,1,3)的矢量就是2个矢量
。这三个矢量取好以后,其它的矢量就可以通过三元数组来表示,因为它们可以表示成一定倍数的三个基本矢量的总合。比如说一个标示为(2,1,3)的矢量就是2个矢量 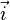 加上1个矢量
加上1个矢量 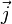 加上3个矢量
加上3个矢量 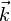 得到的矢量。
得到的矢量。
在进行矩阵运算时,矢量也可以表达成列矢量和行矢量(如下例)。
[编辑]简介
物理学和一般的几何学中涉及的矢量概念严格意义上应当被称为欧几里得矢量或几何矢量,因为它们的定义是建立在通常所说的欧几里得空间上的。按照定义,欧几里得矢量由大小和方向构成。在线性代数中,矢量是所谓矢量空间中的基本构成元素。矢量空间是基于物理学或几何学中的空间概念而形成的一个抽象概念,是满足一系列法则的元素的集合。欧几里得空间便是线性空间的一种。矢量空间中的元素就可以被称为矢量,而欧几里得矢量则是特指欧几里得空间中的矢量。
在一些上下文中,会假设矢量有确定的起点和终点,当起点和终点改变后,构成的矢量就不再是原来的矢量。这样的矢量也被称为固定矢量。在另一些时候,会认为矢量的起点和终点并不那么重要。两个起点不一样的矢量,只要大小相等,方向相同,就可以称为是同一个矢量。这样的矢量被称为自由矢量。在数学中,一般只研究自由矢量。一些文献中会提到矢量空间带有一个特定的原点,这时可能会默认矢量的起点是原点。[1]
[编辑]例子
[编辑]一维矢量
某人家门口是一条南北向的道路。他散步时先向南行走100米,那么他位置的移动就可以用一个大小为100米,方向为南的矢量来表示。之后他再向北走300米,这一次的移动可以用一个大小为300米,方向为北的矢量来表示。散步的人总共相对于他家的位移则可以用大小为200米,方向为北的矢量来表示。几何学上看来,这些矢量都在同一条一维的直线上,只有两个互相平行的方向。
[编辑]物理学的例子
在物理学中,许多常见的量都是用矢量描述,例如运动学中的位移、速度、加速度,力学中的力、力矩,电磁学中的电流密度、磁矩、电磁波等等。其中矢量的大小不一定是表示长度,还可以表示力的大小、电场或磁场的强弱等等。
[编辑]基本性质
矢量的大小是相对的,在有需要时,会规定单位矢量,以其长度作为1。每个方向上都有一个单位矢量[2]。
矢量之间可以如数字一样进行运算。常见的矢量运算有:加法,减法,数乘矢量以及矢量之间的乘法(数量积和矢量积)。
[编辑]加法与减法
矢量的加法满足平行四边形法则和三角形法则。具体地,两个矢量  和
和  相加,得到的是另一个矢量。这个矢量可以表示为
相加,得到的是另一个矢量。这个矢量可以表示为  和
和  的起点重合后,以它们为邻边构成的平行四边形的一条对角线(以共同的起点为起点的那一条,见下图左),或者表示为将
的起点重合后,以它们为邻边构成的平行四边形的一条对角线(以共同的起点为起点的那一条,见下图左),或者表示为将  的终点和
的终点和  的起点重合后,从
的起点重合后,从  的起点指向
的起点指向  的终点的矢量:
的终点的矢量:
两个矢量  和
和  的相减,则可以看成是矢量
的相减,则可以看成是矢量  加上一个与
加上一个与  大小相等,方向相反的矢量。又或者,
大小相等,方向相反的矢量。又或者, 和
和  的相减得到的矢量可以表示为
的相减得到的矢量可以表示为  和
和  的起点重合后,从
的起点重合后,从  的终点指向
的终点指向  的终点的矢量:
的终点的矢量:
当这两个矢量数值、方向都不同,基本矢量  时,矢量和计算为
时,矢量和计算为
并且有如下的不等关系:

[编辑]反矢量和零矢量
与数字一样,一个矢量也有反矢量。一个矢量  的反矢量与它大小相等,但方向相反,一般记作
的反矢量与它大小相等,但方向相反,一般记作  。如果矢量
。如果矢量  是矢量
是矢量  的反矢量,那么
的反矢量,那么  也是
也是  的反矢量[2]。
的反矢量[2]。
零矢量是指大小为零的矢量。零矢量实质上是起点与终点重合的矢量,它的方向是不确定的,可以根据需要假设其方向。两个反矢量的和就是零矢量[2]。
[编辑]标量乘法
一个标量 k 和一个矢量  之间可以做乘法,得出的结果是另一个与
之间可以做乘法,得出的结果是另一个与  方向相同或相反,大小为
方向相同或相反,大小为  的大小的 k 倍的矢量,可以记成
的大小的 k 倍的矢量,可以记成  [2]。-1乘以任意矢量会得到它的反矢量,0乘以任何矢量都会得到零矢量
[2]。-1乘以任意矢量会得到它的反矢量,0乘以任何矢量都会得到零矢量  。
。
[编辑]数量积
数量积也叫点积,它是矢量与矢量的乘积,其结果为一个标量。几何上,数量积可以定义如下:
设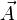 、
、 为两个任意矢量,它们的夹角为
为两个任意矢量,它们的夹角为 ,则他们的数量积为:
,则他们的数量积为:
数量积被广泛应用于物理中,如做功就是用力的矢量点乘位移的矢量,即  。
。
[编辑]矢量积
矢量积也叫叉积,矢量积,它也是矢量与矢量的乘积,不过需要注意的是,它的结果是个矢量,但由于其结果是由坐标系确定,所以其结果被称为伪矢量。
设有矢量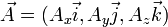 、
、 ,
,
则其矢量积的矩阵表达式可写作:
[编辑]混合积
三个矢量  、
、 和
和  的混合积定义为:
的混合积定义为:
[编辑]线性相关性
对于m个矢量  ,
,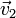 ,……,
,……, ,如果存在一组不全为零的m个数
,如果存在一组不全为零的m个数 、
、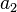 、……、
、……、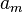 ,使得
,使得  ,那么,称m个矢量
,那么,称m个矢量 ,
,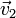 ,……,
,……, 线性相关。如果这样的m个数不存在,即上述矢量等式仅当
线性相关。如果这样的m个数不存在,即上述矢量等式仅当 =
=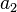 = …… =
= …… = 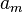 = 0时才能成立,就称矢量
= 0时才能成立,就称矢量 ,
,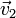 ,……,
,……, 线性无关。[4]
线性无关。[4]
[编辑]矢量与基
矢量空间分为有限维矢量空间与无限维矢量空间。在有限维矢量空间中,可以找到一组(有限个)矢量 ,使得任意一个矢量
,使得任意一个矢量  都可以唯一地表示成这组矢量的线性组合:
都可以唯一地表示成这组矢量的线性组合:
其中的标量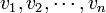 是随着矢量
是随着矢量  而确定的。这样的一组矢量称为矢量空间的基。给定了矢量空间以及一组基后,每个矢量就可以用一个数组来表示了[5]。两个矢量
而确定的。这样的一组矢量称为矢量空间的基。给定了矢量空间以及一组基后,每个矢量就可以用一个数组来表示了[5]。两个矢量  和
和 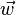 相同,当且仅当表示它们的数组一样。
相同,当且仅当表示它们的数组一样。
两个矢量  和
和 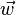 的和:
的和:
它们的数量积为:
而标量k与矢量v的乘积则为:
[编辑]矢量的模长
矢量的大小也叫做范数或模长,记作 。有限维空间中,已知矢量的坐标,就可以知道它的模长:
。有限维空间中,已知矢量的坐标,就可以知道它的模长:









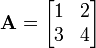



![\begin{array}{lcl}\vec{a} &=& \begin{bmatrix} a\\ b\\ c\\\end{bmatrix} \\\vec{a} &=& [ a\ b\ c ].\end{array}](http://upload.wikimedia.org/math/4/2/4/4242f9825958780458a821da10586fec.png)


























 4001
4001

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








