梯度含义的理解

梯度的概念贯穿很多机器学习算法，理解其概念很重要。但是很多人仍然很迷惑，对梯度和导数的概念混淆不请，这里说下我自己的理解。

首先网络和教材有很多关于梯度的解释，诸如：

1、梯度是某点切平面的法向量，

2、梯度是多元函数增长最快的自变量的方向

3、梯度方向垂直于xoy平面的等高线

一般的认知某点的梯度和某点的导数有很大的联系，其中导数是某条曲线的切线，切线是函数值变化最快的方向，而梯度则是函数值增加最快的方向（增加也是变化），因此直观上讲，在某些情况应该可以认为导数和梯度是一回事（都是使函数值变化最快，不管同向还是反向，至少方向是“共线”的）。但是在梯度的定义这，从1和3的定义可知，法向量，垂直这样的字眼把人整的云里雾里，如下图是两条曲线的梯度方向：

那么，问题到底出在哪？为什么一向认为的切线方向成了垂直呢？

其实，梯度确实是切线方向，只是我们看的所谓法向量，垂直是站在自变量的角度。而切线方向是针对因变量的角度。这句话和第2条解释相通，即梯度是使函数增长（因变量）最快的自变量的方向，简称梯度是函数增长最快的方向。

举例说明：

先以2元函数z=f(x,y)为例，如图。

认知梯度首先明确：自变量是x和y，而因变量（函数）是z，梯度是让z增长最快的方向。

这里在三维坐标系下，z=f(x,y)是一个三维曲面，就好比一座山峰，目前我处于A点，要想让z增长的最快，就沿着图中上山最抖的方向走。此时上山最抖的方向是沿着函数曲面的切线方向，从这里看出梯度还是相切。那么为什么变成垂直方向了呢？

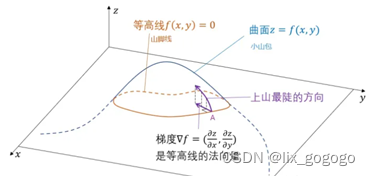
重新看下定义2，梯度是让z增长最快时自变量的方向，也就是x和y的方向。意思是这条切线在x和y的方向是怎么样的，即梯度最后要归结于x, y如何变化。

而要想得到梯度在x,y的方向，可以先投影到xoy平面上，即把曲面降维。因为x, y, z轴相互正交，梯度在z上的投影对梯度在x, y上的分量没作用。

从降维后的曲线可知，现在梯度的方向确实是垂直方向，也可以说是切线（切平面）的法线方向，这还没完，这只是梯度在xoy平面的形态，而非在自变量即x轴和y轴上的体现。此时接分别往x轴和y轴上投影，就得到了x方向的梯度fx'和y方向的梯度fy'。

这里顺便提一下，如果我们认为xoy平面的切线是梯度，则此时的因变量不是z，而是y（x是因变量）或者x（y是自变量）。

所以，在认知梯度时要抓住一点，就是梯度是谁的梯度，谁是因变量。梯度对于因变量而言是切线方向，但是对于降低维度后的自变量组成的空间而言（变成等值线或等值面），梯度是切平面的法线。