Codeforces 821E Okabe and El Psy Kongroo【Dp+矩阵快速幂】套路题

E. Okabe and El Psy Kongroo

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Okabe likes to take walks but knows that spies from the Organization could be anywhere; that's why he wants to know how many different walks he can take in his city safely. Okabe's city can be represented as all points (x, y) such that x and y are non-negative. Okabe starts at the origin (point (0, 0)), and needs to reach the point (k, 0). If Okabe is currently at the point (x, y), in one step he can go to (x + 1, y + 1), (x + 1, y), or (x + 1, y - 1).

Additionally, there are n horizontal line segments, the i-th of which goes from x = a_i to x = b_i inclusive, and is at y = c_i. It is guaranteed that a₁ = 0, a_n ≤ k ≤ b_n, and a_i = b_i - 1 for 2 ≤ i ≤ n. The i-th line segment forces Okabe to walk with y-value in the range 0 ≤ y ≤ c_i when his x value satisfies a_i ≤ x ≤ b_i, or else he might be spied on. This also means he is required to be under two line segments when one segment ends and another begins.

Okabe now wants to know how many walks there are from the origin to the point (k, 0) satisfying these conditions, modulo 10⁹ + 7.

Input

The first line of input contains the integers n and k (1 ≤ n ≤ 100, 1 ≤ k ≤ 10¹⁸) — the number of segments and the destination x coordinate.

The next n lines contain three space-separated integers a_i, b_i, and c_i (0 ≤ a_i < b_i ≤ 10¹⁸, 0 ≤ c_i ≤ 15) — the left and right ends of a segment, and its y coordinate.

It is guaranteed that a₁ = 0, a_n ≤ k ≤ b_n, and a_i = b_i - 1 for 2 ≤ i ≤ n.

Output

Print the number of walks satisfying the conditions, modulo 1000000007 (10⁹ + 7).

Examples

Input

1 3
0 3 3

Output

4

Input

2 6
0 3 0
3 10 2

Output

4

Note

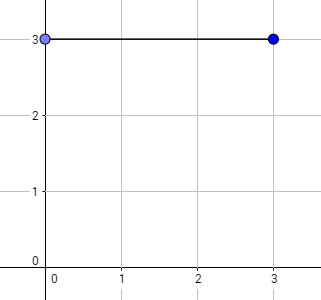
The graph above corresponds to sample 1. The possible walks are:

• 
• 
• 
• 

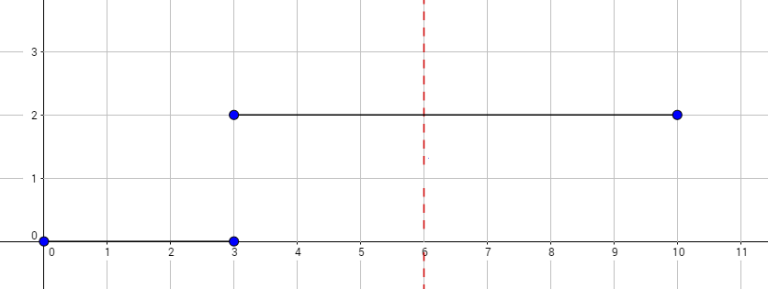
The graph above corresponds to sample 2. There is only one walk for Okabe to reach (3, 0). After this, the possible walks are:

• 
• 
• 
• 

题目大意：

我们现在位于（0,0）处，目标是走到（K，0）处。

每一次我们都可以从（x，y）走到（x+1，y-1）或者（x+1，y）或者（x+1，y+1）三个位子之一。

现在一共有N段线段，每条线段都是平行于X轴的。

我们如果此时x是在这段线段之内的话，我们此时走到的点（x，y）需要满足0<=y<=Ci.

现在保证一段线段的终点，一定是下一段线段的起点。

问我们从起点走到终点的行走方案数。

思路：

看到数据范围，很套路的Dp+矩阵快速幂。

而且这个题的Dp转移方程不难写，其实看起来这个E比D简单的多= =

假设我们此时只有一段线段且K很小，那么我们可以设定Dp【i】【j】表示走到点（i，j）的方案数。

那么很显然Dp【i】【j】+=Dp【i-1】【j】+Dp【i-1】【j-1】+Dp【i-1】【j+1】；

初始化dp【0】【0】=1即可。

然而这里K很大，那么我们对于每一段的状态转移过程使用矩阵快速幂优化一下即可。

设定矩阵的时候，我们就可以忽略掉X轴这个维度，设定dp【i】去转移即可：

过程维护上一次到达线段终点的可行方案数，然后继续转移下一段线段。

直到最终为止。

代码不难实现，稍微注意一点细节。

Wa在了第七组一下，已经标注上Wa点了。在代码中不难理解。

Ac代码：

#include<stdio.h>
#include<string.h>
using namespace std;
#define ll __int64
const ll mod=1000000007;
typedef struct Matrix
{
    ll mat[17][17];
}matrix;
matrix A,B,pre;
Matrix matrix_mul(matrix a,matrix b,ll len)
{
    matrix c;
    memset(c.mat,0,sizeof(c.mat));
    ll i,j,k;
    for(ll i=0;i<=len;i++)
    {
        for(ll j=0;j<=len;j++)
        {
            for(ll k=0;k<=len;k++)
            {
                c.mat[i][j]+=((a.mat[i][k])%mod*(b.mat[k][j])%mod)%mod;
                c.mat[i][j]%=mod;
            }
        }
    }
    return c;
}
Matrix matrix_quick_power(matrix a,ll k,ll len)
{
    matrix b;
    memset(b.mat,0,sizeof(b.mat));
    for(ll i=0;i<=len;i++)
    b.mat[i][i]=1;//单位矩阵b
    while(k)
    {
        if(k%2==1)
        {
            b=matrix_mul(a,b,len);
            k-=1;
        }
        else
        {
            a=matrix_mul(a,a,len);
            k/=2;
        }
    }
    return b;
}
int main()
{
    ll n,end;
    while(~scanf("%I64d%I64d",&n,&end))
    {
        memset(pre.mat,0,sizeof(pre.mat));
        memset(A.mat,0,sizeof(A.mat));
        for(ll i=0;i<16;i++)
        {
            for(ll j=i-1;j<i+2&&j<16;j++)
            {
                if(j>=0&&j<=15)
                {
                    A.mat[i][j]=1;
                }
            }
        }
        ll flag=0;
        pre.mat[0][0]=1;
        for(ll i=1;i<=n;i++)
        {
            ll L,R,y;
            scanf("%I64d%I64d%I64d",&L,&R,&y);
            if(R>end)R=end,flag=1;
            B=matrix_quick_power(A,R-L,y);
            for(ll j=y+1;j<=15;j++)pre.mat[j][0]=0;//Wa 7 的点
            B=matrix_mul(B,pre,y);
            for(ll j=0;j<=y;j++)
            {
                pre.mat[j][0]=B.mat[j][0];
            }
            if(flag==1)break;
        }
        printf("%I64d\n",B.mat[0][0]);
    }
}