题目:有一个棋盘和8个要放到上面的皇后。唯一的要求是皇后之间不能构成威胁。也就是说,必须把它们放置成每个皇后都不能吃掉其他皇后的状态, 怎样才能做到?皇后要如何放置?
分析:这是一个典型的回溯问题,首先尝试放置第一个皇后(在第1行),然后放置第二个,以此类推,如果发现不能放置下一个皇后,就回溯到上一步,试着将皇后放到其他的位置,最后,尝试完所有可能的方案。
在Python中可以使用元组或者列表,每个元组中都表示相应行的皇后的位置(即列)。例如,state[0] == 3表示在第一行的皇后在第四列(从0开始计数)。
实现代码:
首先寻找冲突:由conflict函数判断下一个的皇后的位置会不会有新的冲突。如果下一个皇后和前面的皇后有同样的水平位置,或者在一条对角线上,就会发生冲突,则返回True。
接着使用递归来寻找每一个皇后能够占据的合适的位置。
最后由函数prettyprint形象地打印出一个解决方案。
def conflict(state, nextX):
nextY = len(state)
for i in range(nextY):
if abs(state[i]-nextX) in (0, nextY-i):
return True
return False
def queens(num = 8, state = ()):
for pos in range(num):
if not conflict(state, pos):
if len(state) == num-1:
yield (pos,)
else:
for result in queens(num, state+(pos,)):
yield (pos,)+result
def prettyprint(solution):
def line(pos, length=len(solution)):
return '.'*pos+'X'+'.'*(length-pos-1)
for pos in solution:
print line(pos)
运行结果如下:
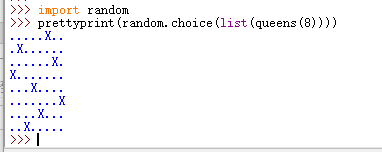
是不是很有趣呢~~






















 144
144

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








