【Graph Neural Network 图神经网络】2.Spectral-based Graph Convolutional Networks 基于谱域的图卷积网络

一、图卷积网络（GCN）

卷积图神经网络（GCN，图卷积网络）与递归图神经网络关系密切。与使用收缩约束迭代节点状态不同，ConvGNNs在架构上使用具有固定数量的不同卷积层来处理循环相互依赖，下图说明了这一关键区别。由于图卷积与其他神经网络的融合更加高效方便，近年来它的普及率迅速提高。

GCN可分为两类，基于谱域Spectral的和空间Spatial的。基于谱域的方法从图信号处理的角度引入滤波器来定义图卷积，其中图卷积运算被解释为从图信号中去除噪声。而基于空间的方法继承了RecGNNs的思想，通过信息传播来定义图卷积。
本文主要介绍基于谱域的图卷积网络。

---

二、谱域理论基础

这一节内容主要参考https://www.zhihu.com/question/54504471/answer/332657604，在此简略阐述一遍。
一句话总结基于谱域的图卷积：对节点特征$f$进行傅里叶变换后，生成以拉普拉斯矩阵的特征向量为基的谱图，然后依据卷积定理求得卷积核$g$对$f$卷积后提取的特征。

0. 基本概念

图用$G=(V,E)$表示，$V$中元素为节点（vertex），$E$中元素为边（edge）。按照边是否有指向性分为有向图和无向图，按照边是否有权值分为有权图和无权图。
度矩阵$D$表示对角阵，对角上的元素为各个节点的度。顶点$v_i$的度表示和该顶点相关联的边的数量。
邻接矩阵$A$表示节点间的连接关系，是n阶方阵（n为节点数量）。无向图邻接矩阵是对称矩阵，而有向图的邻接矩阵不一定对称。无权图的邻接矩阵由0和1组成，有权图会依据权值变化。

1. 拉普拉斯矩阵（Laplacian）

常用的拉普拉斯矩阵有三种，这里用到了前两种，分别是标准和归一化后的形态：

1. Combinatorial Laplacian: $L=D-A$
2. Symmetric normalized Laplacian: $L_{sys}=D^{-\frac{1}{2}}L{D}^{-\frac{1}{2}}$
   
   为什么要用拉普拉斯矩阵？因为它是半正定对称矩阵，可以进行特征分解，且一定有$n$个线性无关相互正交的特征向量，构成的矩阵$U$为正交矩阵，满足$U{U}^T=E$，所以有：
   $$L=U\left(\begin{array}{ccc}{\lambda }_1& & \\ & \ddots & \\ & & {\lambda }_n\end{array}\right)U^{-1}=U\left(\begin{array}{ccc}{\lambda }_1& & \\ & \ddots & \\ & & {\lambda }_n\end{array}\right)U^T$$

2. 傅里叶变换（Fourier Transform）

传统的傅里叶变换定义为：
$$F(w)=ϝ[f(t)]=\int f(t)e^{-iwt}dt$$其中$e^{-iwt}$是信号$f(t)$的基函数，也是拉普拉斯算子的特征函数。

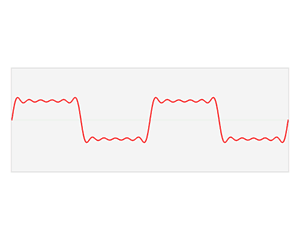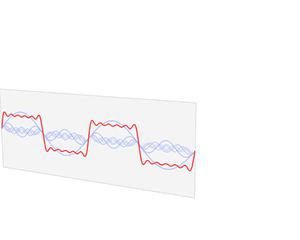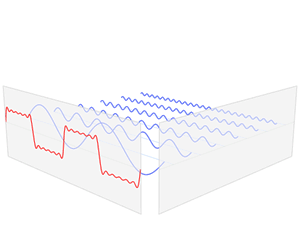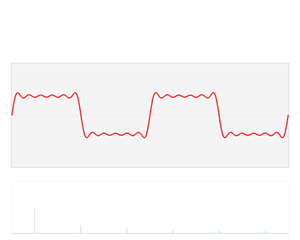
如何把传统的傅里叶变换以及卷积迁移到图上？核心工作就是把$e^{-iwt}$类推为图对应的拉普拉斯矩阵的特征向量。
传统傅里叶变换是连续形式的，在处理图时用到的是傅里叶变换的离散形式。由于拉普拉斯矩阵进行特征分解以后，可以得到$n$个线性无关的特征向量，构成空间中的一组正交基，因此归一化拉普拉斯矩阵算子的特征向量构成了图傅里叶变换的基。图傅里叶变换将输入图的信号投影到了正交空间，相当于把图上定义的任意向量，表示成了拉普拉斯矩阵特征向量的线性组合。
由此定义图上的傅里叶变换：
$$F({\lambda }_l)=\hat{f}({\lambda }_l)=\sum _{i=1}^{N}f(i)u_l(i)$$其中，是$f$是图上的$N$维向量，$f(i)$表示图中某个节点的特征，$u_l(i)$表示第$l$个特征向量的第$i$个分量，那么特征值（频率）${\lambda }_l$下的，$f$的图傅里叶变换就是与${\lambda }_l$对应的特征向量$u_l$进行内积运算。
利用矩阵乘法将Graph上的傅里叶变换推广到矩阵形式：$$\hat{f}=U^{T}f$$
同理，传统的傅里叶逆变换是对频率$w$求积分：$${ϝ}^{-1}[F(w)]=-\frac{1}{2\Pi }\int F(w)e^{-iwt}dw$$迁移到Graph上变为对特征值${\lambda }_l$求和：
$$f(i)=\sum _{l=1}^N\hat{f}({\lambda }_l)u_l(i)$$利用矩阵乘法将图上的傅里叶逆变换推广到矩阵形式：
$$f=U\hat{f}$$

3. 卷积

卷积定理：函数卷积的傅里叶变换是函数傅立叶变换的乘积，即对于函数 $f(t)$与$g(t)$两者的卷积是其函数傅立叶变换乘积的逆变换：
$$f\ast g={ϝ}^{-1}(ϝ(f)\cdot ϝ(g))$$结合前文关于图傅里叶变换和逆变换的定义有：
f ∗ g = U ( ( U T f ) ⋅ ( U T g ) ) f*g=U((U^Tf)\cdot(U^Tg)) f∗g=U((UTf)⋅(<