一. 引入
赫夫曼(Huffman)树又称最优二叉树,也就是带权路径最短的树。
二. 概念
有几个概念,在wiki上也有说明:
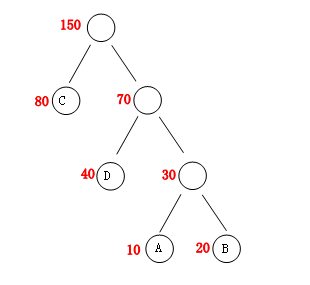
节点的权: 节点中红色部分就是权,在实际应用中,我们用“字符”出现的次数作为权。
路径长度:可以理解成该节点到根节点的层数,比如:“A”到根节点的路径长度为3。
树的路径长度:各个叶子节点到根节点的路径长度总和。
赫夫曼树也就是带权路径长度最小的一棵树。
三.示例
构建Huffman树
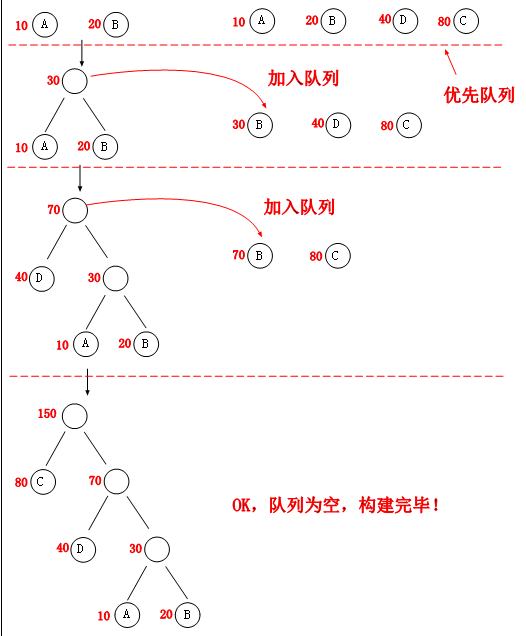
Huffman树的构建采用自低向上的方式,这里采用优先级队列(Java.util.PriorityQueue)来存放当前需要构建的节点。也可以自己实现完全二叉树(full binary tree)来实现构建Huffman树。
构建过程图示
四.应用
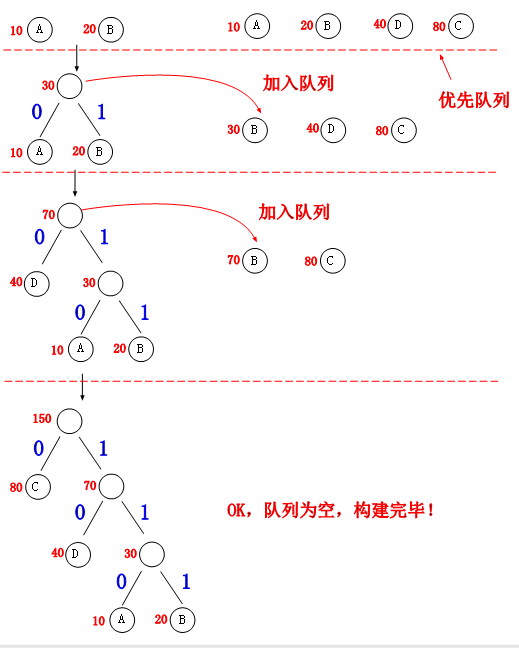
Huffman树的典型应用就是在数据压缩方面,下面我们就要在赫夫曼树上面放入赫夫曼编码了,我们知道普通的ASCII码是采用等长编码的,即每个字符都采用2个字节,而赫夫曼编码的思想就是采用不等长的思路,权重高的字符靠近根节点,权重低的字符远离根节点,标记方式为左孩子“0”,右孩子“1”,如下图。
从图中我们可以看到各个字符的赫夫曼编码了,获取字符的编码采用从根往下的方式收集路径上的‘0,1’,如:
A:110。
B:111。
C:0。
D:10。
最后我们来比较他们的WPL的长度:
ASCII码=10*2+20*2+40*2+80*2=300
Huffman码=10*3+20*3+40*2+80*1=250
可以看到,赫夫曼码压缩了50个0,1字符,太牛逼了,是吧。
五.编码
1.构建Huffman树代码
private static Tree buildTree(Map<Character, Integer> statistics, List<Node> leafs) {
Character[] keys = statistics.keySet().toArray(new Character[0]);
PriorityQueue<Node> priorityQueue = new PriorityQueue<>();
for (Character character : keys) {
Node node = new Node();
node.chars = character.toString();
node.frequence = statistics.get(character);
priorityQueue.add(node);
leafs.add(node);
}
int size = priorityQueue.size();
for (int i = 1; i <= size - 1; i++) {
Node node1 = priorityQueue.poll();
Node node2 = priorityQueue.poll();
Node sumNode = new Node();
sumNode.chars = node1.chars + node2.chars;
sumNode.frequence = node1.frequence + node2.frequence;
sumNode.leftNode = node1;
sumNode.rightNode = node2;
node1.parent = sumNode;
node2.parent = sumNode;
priorityQueue.add(sumNode);
System.out.println("sumNode:" + sumNode + " leftNode:" + node1 + " rightNode:" + node2);
}
Tree tree = new Tree();
tree.root = priorityQueue.poll();
return tree;
}
2.压缩和解压缩
public static String encode(String originalStr, Map<Character, Integer> statistics) {
if (originalStr == null || originalStr.equals("")) {
return "";
}
char[] charArray = originalStr.toCharArray();
List<Node> leafNodes = new ArrayList<Node>();
buildTree(statistics, leafNodes);
Map<Character, String> encodInfo = buildEncodingInfo(leafNodes);
StringBuffer buffer = new StringBuffer();
for (char c : charArray) {
Character character = new Character(c);
buffer.append(encodInfo.get(character));
}
return buffer.toString();
}
private static Map<Character, String> buildEncodingInfo(List<Node> leafNodes) {
Map<Character, String> codewords = new HashMap<>();
for (Node leafNode : leafNodes) {
Character character = new Character(leafNode.getChars().charAt(0));
String codeword = "";
Node currentNode = leafNode;
try {
do {
if (currentNode.isLeftChild()) {
codeword = "0" + codeword;
} else {
codeword = "1" + codeword;
}
currentNode = currentNode.parent;
} while (currentNode.parent != null);
} catch (Exception e) {
e.printStackTrace();
}
codewords.put(character, codeword);
}
return codewords;
}
public static String decode(String binaryStr, Map<Character, Integer> statistics) {
if (binaryStr == null || binaryStr.equals("")) {
return "";
}
char[] binaryCharArray = binaryStr.toCharArray();
LinkedList<Character> binaryList = new LinkedList<>();
int size = binaryCharArray.length;
for (int i = 0; i < size; i++) {
binaryList.addLast(new Character(binaryCharArray[i]));
}
List<Node> leafNodes = new ArrayList<>();
Tree tree = buildTree(statistics, leafNodes);
StringBuffer buffer = new StringBuffer();
while (binaryList.size() > 0) {
Node node = tree.root;
do {
Character c = binaryList.removeFirst();
if (c.charValue() == '0') {
node = node.leftNode;
} else {
node = node.rightNode;
}
} while (!node.isLeaf());
buffer.append(node.chars);
}
return buffer.toString();
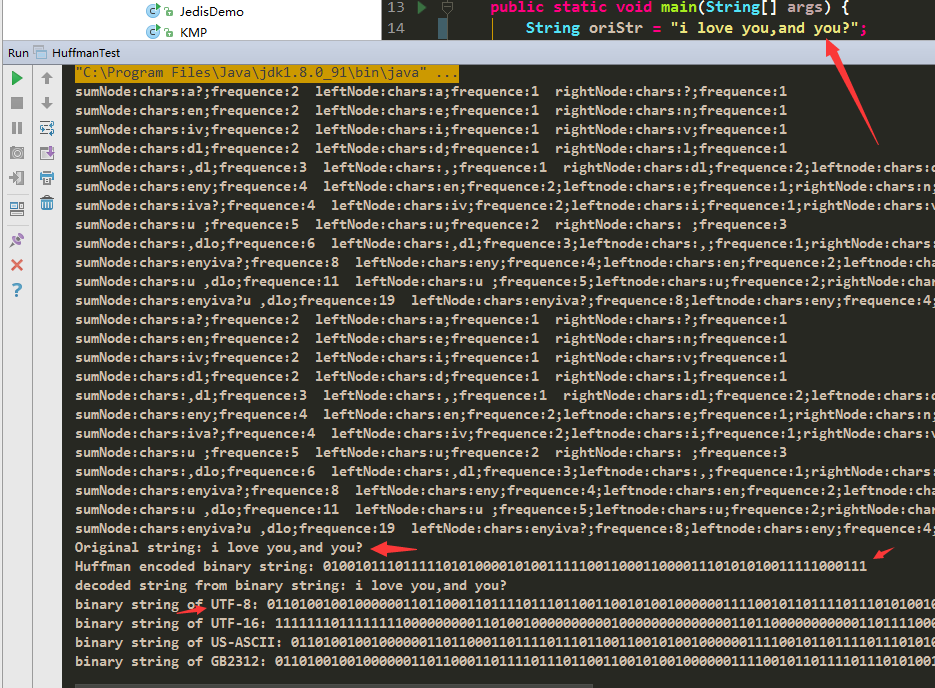
}结果是:
具体代码见我的github。
参考文献:
1. Huffman coding:http://rosettacode.org/wiki/Huffman_coding
2. wiki:https://en.wikipedia.org/wiki/Huffman_coding






















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








