有趣“树”——线段树

线段树

一.为什么要用它

一. 为什么要用它：
题目一：

1.求一个整形数组arr中arr[L]到arr[R]的数据之和，0 < L && L<= R && R < 5.
2.将整形数组arr中arr[3]修改为6。

解：
第一题的时间复杂度为O（n）需要一个个相加
第二题的时间复杂度为O（1）直接通过下标修改

题目二：arr2[n]=arr[0]+arr[1]+…+arr[n]

1.已知数组arr2，求一个整形数组arr中arr[L]到arr[R]的数据之和，0 < L && L<= R && R < 5.
2.已知数组arr2，将整形数组arr中arr1[3]修改为6,求arr2。

解：
第一题的时间复杂度为O（1）只需通过下标arr[R]-arr[L]则可得到数据
第二题的时间复杂度为O（n）更新完arr的数据，arr2需要需要n次修改

线段树可以将上述题目的时间复杂度缩减为O（log2）

二.创建线段树

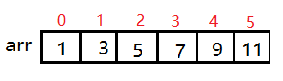
如图，有一组数组，我们如何将它转化为线段树呢？
线段树也是一种二叉树，父节点为子节点的和；
mid=（L+R）/2；
left_node = node * 2 + 1;
right_node = node * 2 + 2;
最终构建出线段树，如下图：

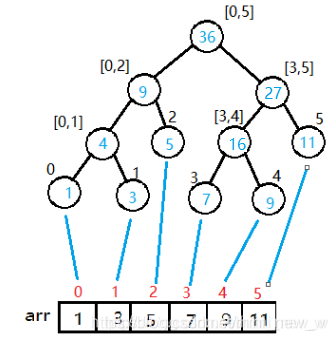
代码实现：

#include <iostream>
#include <stdio.h>
using namespace std;
#define MAX_LEN 100  //给tree一个尽量大的内存
/*
函数名：build_tree
作用：创建线段树
参数：arr[]:数组,tree[]：树,node：根结点,start：区间左边L,end：区间右边R
返回值：无
*/
void build_tree(int arr[], int tree[], int node, int start, int end) {
	if (start == end) {              //到达子节点
		tree[node] = arr[start];
	}
	else {
		int left_node = node * 2 + 1;
		int right_node = node * 2 + 2;
		int mid = (start + end) / 2;
		build_tree(arr, tree, left_node, start, mid);
		build_tree(arr, tree, right_node, mid + 1, end);
		tree[node] = tree[left_node] + tree[right_node];
	}
}

int main() {
	int arr[] = { 1, 3, 5, 7, 9, 11 };
	int size = 6;
	int tree[MAX_LEN] = { 0 };
	build_tree(arr, tree, 0, 0, size - 1);
	//打印观察结果
	for (int i = 0; i < 15; i++) {
		printf("tree[%d] = %d\n", i, tree[i]);
	}
	return 0;
}

结果：与tree数组一样

三.更新线段树

更新：arr[4] = 10，更新步骤如图：

代码实现：

#include <iostream>
#include <stdio.h>
using namespace std;
#define MAX_LEN 100  //给tree一个尽量大的内存
/*
函数名：build_tree
作用：创建线段树
参数：arr[]:数组,tree[]：树,node：根结点,start：区间左边L,end：区间右边R
返回值：无
*/
void build_tree(int arr[], int tree[], int node, int start, int end) {
	if (start == end) {              //到达子节点
		tree[node] = arr[start];
	}
	else {
		int left_node = node * 2 + 1;
		int right_node = node * 2 + 2;
		int mid = (start + end) / 2;
		build_tree(arr, tree, left_node, start, mid);
		build_tree(arr, tree, right_node, mid + 1, end);
		tree[node] = tree[left_node] + tree[right_node];
	}
}
/*
函数名：update_tree
作用：更新线段树
参数：arr[]:数组,tree[]：树,node：根结点,start：区间左边L,end：区间右边R,idx:要更新的数组下标，val：更新后的数值
返回值：无
*/
void update_tree(int arr[], int tree[], int node, int start, int end, int idx, int val) {
	if (start == end) {              //到达子节点
		arr[idx] = val;
		tree[node] = val;
	}
	else
	{
		int mid = (start + end) / 2;
		int left_node = node * 2 + 1;
		int right_node = node * 2 + 2;
		if (idx > start && idx <= mid)
			update_tree(arr, tree, left_node, start, mid, idx, val);
		else
			update_tree(arr, tree, right_node, mid + 1, end, idx, val);
		tree[node] = tree[left_node] + tree[right_node];
	}
}
int main() {
	int arr[] = { 1, 3, 5, 7, 9, 11 };
	int size = 6;
	int tree[MAX_LEN] = { 0 };
	build_tree(arr, tree, 0, 0, size - 1);   //构建线段树
	//打印观察结果
	/*for (int i = 0; i < 15; i++) {
		printf("tree[%d] = %d\n", i, tree[i]);
	}
	printf("\n");*/
	update_tree(arr, tree, 0, 0, size - 1, 4, 10);  //更新线段树
	//打印观察结果
	for (int i = 0; i < 15; i++) {
		printf("tree[%d] = %d\n", i, tree[i]);
	}
	return 0;
}

结果：与跟新后的tree一样：

四.区间更新

五.区间之和

求arr[2]到arr[5]的和

/*
函数名：query_tree
作用：求区级线段树
参数：arr[]:数组,tree[]：树,node：根结点,start：区间左边L,end：区间右边R,L:区间左端点，R：区间右端点
返回值：无
*/
int query_tree(int arr[], int tree[], int node, int start, int end, int L, int R) {
	if (R < start || L > end)
		return 0;
	else if (start >= L && end <= R)
		return tree[node];
	else if (start == end) 
		return tree[node];
	else{
		int mid = (start + end) / 2;
		int left_node = node * 2 + 1;
		int right_node = node * 2 + 2;
		int sum_left = query_tree(arr, tree, left_node, start, mid, L, R);
		int sum_right = query_tree(arr, tree, right_node, mid + 1, end, L, R);
		return sum_left + sum_right;
	}
}

int main() {
	int arr[] = { 1, 3, 5, 7, 9, 11 };
	int size = 6;
	int tree[MAX_LEN] = { 0 };
	build_tree(arr, tree, 0, 0, size - 1);   //构建线段树
	
	int s = query_tree(arr, tree, 0, 0, size - 1, 2, 5);
	//打印观察结果
	printf("query_tree = %d", s);
	return 0;
}