从零开始使用matlab实现EKF-SLAM算法（含完整代码）

mjmmm

于 2024-04-27 13:59:06 发布

阅读量1.7k

点赞数 15

文章标签： matlab 算法卡尔曼滤波器扩展卡尔曼 EKF SLAM EKF-SLAM

本文链接：https://blog.csdn.net/mjmmm/article/details/138174505

版权

EKF-SLAM算法

在机器人和自主导航领域，准确的测绘和定位对于成功运行至关重要。在为此目的开发的各种算法中，扩展卡尔曼滤波器 (EKF) 因其在处理与现实世界动态相关的非线性方面的有效性而脱颖而出。 EKF 是卡尔曼滤波器的扩展，可对当前均值和协方差的估计进行线性化，使其适用于需要精度和可靠性的各种应用。
扩展卡尔曼滤波器同步定位与建图 (EKF-SLAM) 算法建立在 EKF 的基础上，集成了 EKF 的功能，可解决机器人技术中最具挑战性的问题之一：同时定位与建图 (SLAM)。 EKF-SLAM采用EKF方法来同时估计机器人的状态和周围环境的布局，而无需事先了解位置。这种双重功能对于在未知环境中运行的自主系统至关重要，使它们能够在绘制区域地图时有效导航。 EKF-SLAM 算法一直是自动驾驶车辆和机器人系统开发的基石，为处理现实世界环境中固有的不确定性提供了一个强大的框架。

坐标系定义和机器人模型

1. 坐标系定义

在本项目中，我在全局坐标中定义了小车的状态转换模型和观察模型。在我的定义中，左方向被认为是正方向，车辆在时间 $k$ 的方向表示为 $\theta {_{k}}$ ，定义为车辆的航向轴与全局坐标y轴之间的角度，且向左偏转为正。

2. 汽车状态转移模型

$x_{k}$ 是状态向量
$u_{k,T}$ 是控制向量
$\Delta S$ 是单位时间内移动的距离，其值为 $V\cdot d_{t}$ （速度 x 时间）
$\Delta \theta$ 是单位时间内车辆的角度变化，也就是舵角
$\theta {_{k}}$ 是车辆在时间 $k$ 时基于y轴正方向的角度，向左偏转为正
$V$ （速度）和 $\Delta \theta$ （舵角）都包含均值为0，方差为 $Q$ 的高斯白噪声
加上 $\frac{\pi }{2}$ 是为了将相对于y轴的角度转化为相对于x轴的角度，保证cos和sin的计算值正确

3. 观测模型

$Z_{r}^{(i)}$ 是第 $i$ 个路标(landmark)和车辆当前坐标的距离
$Z_{\theta}^{(i)}$ 是第 $i$ 个路标(landmark)和车辆当前坐标的角度差
$I_{kx}^{(i)}$ 和 $I_{ky}^{(i)}$ 分别是第 $i$ 个路标(landmark)的真实 $x$ 和 $y$ 坐标
$x{_{k}}$ 和 $y{_{k}}$ 分别是车辆当前的 $x$ 和 $y$ 坐标
$\theta {_{k}}$ 是车辆在时间 $k$ 时基于y轴正方向的角度，向左偏转为正
$v_{k}$ 是均值为0，方差为 $R$ 的高斯白噪声
减去 $\frac{\pi }{2}$ 是为了将相对于x轴的角度转化为相对于y轴的角度，保证 $Z_{\theta}^{(i)}$ 的定义不会出错

EKF-SLAM状态变量定义

1. 系统的状态变量

$m_{n,x}$ 和 $m_{n,y}$ 是第 $n$ 个被观测到的路标的 $x$ 和 $y$ 值，也就是说，此处的坐标和路标的真实坐标在有噪声的情况下是不会完全相同的

2. 系统的控制变量

$V$ = 速度
$\Delta \theta$ = 舵角

3. 系统方程

$x_{t}=g(x_{t-1},u_{t})+Q$

$z_{t}=h(x_{t})+R$

$Q$ 和 $R$ 分别是模型的过程噪声和测量噪声
显然， $g(\cdot )$ 和 $h(\cdot )$ 对应的就是刚刚的车辆状态转移模型和测量模型，而这两个模型也显然是非线性的

对于以上这个非线性系统，直接使用传统的卡尔曼滤波是不行的，因为其只针对线性系统，比如下图：

所以，需要先对非线性系统进行局部的线性化，将线性化周围的系统状态看作是线性系统，这样对于非线性不太强的系统，可以认为线性化点周围的系统状态是满足卡尔曼滤波算法的条件的。而扩展卡尔曼算法（EKF）正是这样的一种算法。

扩展卡尔曼算法所使用的线性化方法为泰勒展开。对于非线性系统 $g(\cdot )$ 和 $h(\cdot )$ 进行一阶泰勒展开：

线性化后的扩展卡尔曼算法可以表述如下：

其中，除了刚刚提到的变量之外，中间变量 $K_{t}$ 是卡尔曼增益，算法不断更新的是状态变量 $\mu$ 和协方差矩阵 $\Sigma$

在本项目的EKF-SLAM算法中，和EKF相同，其核心就是不断更新状态变量 $x$ 和协方差矩阵 $\Sigma$ :

若令：

则需要更新的状态变量 $x$ 和协方差矩阵 $\Sigma$ 可以进一步简化表示为：

Q：那么具体如何更新这两个矩阵呢？

A：大致上，使用的是EKF的更新公式，但是由于现在结合了SLAM，所以需要在EKF的基础修改原来的更新细则，增加SLAM的内容，详见接下来的“算法详解”

EKF-SLAM 算法详解

1. 预测阶段

在预测阶段，需要按照刚刚提到的EKF预测公式来更新状态变量和协方差矩阵：

对于本项目，这个式子只需替换我定义的状态变量和我定义过程噪声矩阵Q

$\bar{x_{t}}=g(x_{t-1},u_{t})$

$\bar{\Sigma _{t}}=G_{t}\Sigma _{t-1}G_{t}^{T}+Q_{t}$

1-1. 状态变量更新

由于路标是静止的，所以状态变量只需要根据车辆状态转移模型更新前三行：

1-2. 协方差矩阵更新

同样，由于路标是静止的，所以协方差矩阵中的 $\Sigma _{mm}$ 不需要更新，只需要考虑剩下三个子矩阵。

根据公式，需要计算的是雅可比矩阵 $G_{t}$ 和过程噪声的协方差矩阵 $Q_{t}$

1-2-1. 雅可比矩阵 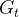$G_{t}$ 的计算

其中：

1-2-2. 过程噪声的协方差矩阵 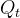$Q_{t}$ 的计算

其中：

但是，由于已知的Q是关于控制量的过程噪声，所以现在x，y，θ的方差并不知道，只知道控制量：速度V和舵角Δθ的方差，所以需要通过下式将控制量的协方差矩阵映射到状态变量：

其中：

现在，就可以根据以上求出的这些矩阵来计算新的协方差矩阵 $\Sigma _{t}$ 了！

2. 更新阶段

在预测阶段，需要按照刚刚提到的EKF更新公式来对状态变量和协方差矩阵进行修正：

对于本项目，这个式子只需替换我定义的状态变量和测量噪声矩阵R

2-1 卡尔曼增益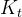 $K_{t}$ 的计算

根据公式，卡尔曼增益的计算需要观测模型的雅可比矩阵 $H_{t}$ 和测量噪声的协方差矩阵 $R_{t}$

其中，由于已知的R本身就是关于 $Z_{r}$ 和 $Z_{\theta }$ 的测量噪声，所以测量噪声的协方差矩阵 $R_{t}$ 可以直接表示为：

观测模型的雅可比矩阵 $H_{t}$ 的计算如下：

首先，定义 $\delta _{x}$ 和 $\delta _{y}$ 分别是车辆当前坐标到观测到的路标(landmarks)坐标的相对距离：

并且假设状态向量为：

然后 $H_{t}$ 的计算如下：

在这个式子中， $H_{t}^{i}$ 是对于只有一个路标 $i$ 时的雅可比矩阵，但是在实际观测中，大多数情况下观测到的路标不止一个，真实的状态向量是：

假设观测到的landmark（路标）序列是：

现在，假设路标序列 $Z_{t}$ 中的第 $i$ 个观测值对应于 $x_{t}$ 中的第j个路标观测值 $m_{j,x}$ ， $m_{j,y}$ ，则可以使用一个数组 $c$ 来表达这种映射关系：

这里有两点需要注意：

当车辆观测到新的路标时，路标序列中的路标在状态变量中找不到对应
车辆观测到的路标坐标是带噪声的，也就是说：如果在两个不同的时间步观察到了同一个路标坐标，返回的值也不是完全相同的，如果严格按照数值是否相同来判断是否是新路标，将会造成大量重复的误判，所以在更新阶段之前，需要进行数据关联

假设现在已经通过数据关联找到了对应的关系，对于已经关联完成的观测值可以进行下一步的推导：

刚刚我们已经计算了对于只有一个路标 $i$ 时的雅可比矩阵 $H_{t}^{i}$ ：

对于多个路标的情况下，由于路标是静止的，任意路标之间没有联系，因此第 $i$ 个路标的雅可比矩阵 $H_{t}^{i}$ 对于其他路标的相关偏导数全为0。由此，可以得出：当有多个路标时，第i个路标的雅可比矩阵 $H_{t}^{i}$ （注意刚刚 $H_{t}^{i}$ 的定义是只有一个路标，现在有区别）的值为：

其中 $F_{j}$ 为：

那么此时，对于更新阶段来说，总体步骤就是：对于已经完成数据关联的观测值进行遍历，对于每一个观测值计算其对应的 $H_{t}^{i}$ ，并由此计算对应的卡尔曼增益，然后根据卡尔曼增益来更新状态向量和协方差矩阵。假设完成数据关联的观测值有n个，则会计算n次 $H_{t}^{i}$ ，计算n次卡尔曼增益，最后更新n次状态向量和协方差矩阵。

3. 数据关联

回顾刚刚在提到路标序列和状态向量中的路标的对应关系中，提到：

当车辆观测到新的路标时，路标序列中的路标可能在状态变量中找不到对应
车辆观测到的路标坐标是带噪声的，也就是说：如果在两个不同的时间步观察到了同一个路标坐标，返回的值也不是完全相同的，如果严格按照数值是否相同来判断是否是新路标，将会造成大量重复的误判，所以在更新阶段之前，需要进行数据关联

数据关联的任务是：找到一种计算路标坐标之间相似度的方法，同时定义阈值，若相似度小于某个阈值，则判定为同一个路标；若大于某个阈值，则判定为新的路标；否则丢弃这个观测值。

这样做可以大大提升计算的效率，减少了由于噪声存在对于同一路标进行反复识别并误判的计算量浪费。

为了减小噪声和角度量纲不一致的影响，使用马氏距离而不是传统的欧氏距离来计算相关性，马氏距离定义如下:

$\vec{x}$ 和 $\vec{y}$ 属于同一分布
$S$ 代表该分布的协方差矩阵

3-1. 具体步骤伪代码

4. 状态向量增广

在数据关联阶段，返回了数据关联的结果，其中，对于成功找到关联的路标，可以进行EKF的更新。但如果更新之后直接进行下一步的预测，那么状态变量的路标数就永远都不会变了，这是因为还没有处理那些被判定为新的路标的路标值。所以此时需要在下一步的EKF预测之前，进行状态向量的增广，顾名思义，这一步就是将新观测到的路标(landmark)信息添加到状态向量及协方差矩阵
中，改变 $x$ 和Σ 的维度。

4-1 改变状态向量的维度

在已知新的路标的相对应 $Z_{r}$ 和 $Z_{\theta}$ 后，状态向量只需要根据观测模型公式来更新就可以了。

当然，新的路标可能不止一个，只需要遍历新的路标，然后一个个添加到状态变量中去就可以，对于每个新的路标值 $Z_{r}$ 和 $Z_{\theta}$ ，状态变量都需要更新两行：

4-2 改变协方差矩阵的维度

协方差矩阵的维度更新要稍微复杂一些，对于每一个新的路标值，首先需要对状态变量新增的两行组成的矩阵进行线性化，所以需要分别求这个矩阵对于 $x_{v}$ 和 $z$ 的雅可比矩阵：

回忆协方差矩阵的组成：

若令：

则需要更新的协方差矩阵 $\Sigma$ 可以进一步简化表示为：

此时，需要更新的是协方差矩阵中与路标相关的部分： $\Sigma _{x_{v}m}$ ， $\Sigma _{mx_{v}}$ ， $\Sigma _{mm}$ ，这些部分可以通过上面求的两个雅可比矩阵将观测模型的协方差矩阵和汽车运动模型的协方差矩阵转化到其对应的相关系数。

对于每一个新的landmark，协方差矩阵的更新流程如下：

Matlab代码结构

在我的项目中，代码总体分为两个阶段：数据生成阶段和算法实施阶段，总体上来说，数据生成阶段先生成真实的路径，以及对应时间步带噪声的变量。在算法实施阶段遍历刚刚的每一个时间步，在每一步中使用带噪声的变量进行EKF-SLAM算法。

数据生成阶段

算法实施阶段

Matlab完整代码

clc;
close all;
clear all;

% 模拟文件控制参数
GATE_REJECT = 4.0; % 判断为已知特征的最大距离
GATE_AUGMENT = 25.0; % 判断为新特征的最小距离

% 控制参数
V = 8; % m/s, 速度 %8, 越小稳定性越强
MAXG = 30*pi/180; % rad, 最大转向角
RATEG = 20*pi/180; % rad/s, 最大转向率
DT_CONTROLS = 0.025; % 控制频率

% 控制噪声参数
Q = [0.002^2 0; 0 (0.008* (pi/180))^2]; % 过程噪声的协方差矩阵
%Q = [20^2 0; 0 (0.008* (pi/180))^2];
%Q = [50^2 0; 0 (0.008* (pi/180))^2];

% 观测噪声
R = [0.5^2 0; 0 (pi/180)^2]; % 观测噪声的协方差矩阵

% 观测参数
MAX_RANGE = 30.0; % 米, 最大观测距离
DT_OBSERVE = 8*DT_CONTROLS; % 秒, 观测频率

% 生成运动轨迹的关键点
t = 0:0.8:6.28;
radius = 40;
data = [radius*cos(t); radius*sin(t)];
key_points = data + radius + 6;

% 生成地标
n_landmarks = 60; % 60个地标
border = [30, 30];
minpos = min((key_points'));
maxpos = max((key_points'));
minlm = minpos - border;
maxlm = maxpos + border;
landmarks(1, :) = minlm(1) + rand(n_landmarks, 1) * (maxlm(1) - minlm(1));
landmarks(2, :) = minlm(2) + rand(n_landmarks, 1) * (maxlm(2) - minlm(2));

% 获取状态
dt = DT_CONTROLS; % 控制频率
iwp = 1; % 初始路径点
G = 0; % 初始转向角
xtrue = [key_points(:, 1); pi/4]; % 初始位置
wp = key_points; % 路径点
dtsum = DT_OBSERVE + 0.0001;

% 根据无噪声的速度、舵角和车辆状态转换模型，获取每一步的真实值和带噪声的速度、舵角及测量值
i = 1;
k = 1;
while iwp ~= 0 % 当iwp为零时退出循环
    
    [G, iwp] = compute_steering(xtrue, wp, iwp, G, RATEG, MAXG, dt); % 更新转向角
    
    xtrue = vehicle_model(xtrue, V, G, dt);  % 更新车辆的真实位置
    
    % 更新收集的控制变量，添加控制噪声
    Vn = V + randn(1) * sqrt(Q(1, 1));
    Gn = G + randn(1) * sqrt(Q(2, 2));
  
    ob = 0;
    dtsum = dtsum + dt;
    
    % 当累计时间dtsum达到指定的观测频率DT_OBSERVE时，重置时间累加器并执行以下操作
    % 效果是每个观测周期进入一次
    if dtsum >= DT_OBSERVE 
        dtsum = 0;
        % 获取当前姿态与所有地标之间的相对x和y距离
        dx = landmarks(1, :) - xtrue(1);
        dy = landmarks(2, :) - xtrue(2);
        phi = xtrue(3);

        % 车辆前方半圆，半径为最大观测距离的范围内的路标
        ii = find((dx*sin(phi) + dy*cos(phi)) > 0 ...  % 地标是否在当前姿态前方?
              & (dx.^2 + dy.^2) < MAX_RANGE^2);            % 地标是否在当前姿态的最大观测距离内？
        
        dx1 = landmarks(1, ii) - xtrue(1);
        dy1 = landmarks(2, ii) - xtrue(2);
        z = [sqrt(dx1.^2 + dy1.^2); atan2(dy1, dx1) - phi - pi/2]; 
     
        
        % 添加观测噪声
        len = size(z, 2);
        if len > 0
            z(1, :) = z(1, :) + randn(1, len) * sqrt(R(1, 1));
            z(2, :) = z(2, :) + randn(1, len) * sqrt(R(2, 2));
        end
        % z现在是带噪声的观测

        ob = 1;  
        i = i + 1;   
    end
    
    % 收集数据
    state.xtrue = xtrue;
    state.Vn = Vn;
    state.Gn = Gn;
    state.zn = z;
    state.observation_update = ob;
    state.next_keypoint = iwp;
    data_original.states(k) = state;

    pause(0.00001); 
    k = k + 1;
end

states = data_original.states;
% 状态获取完成

% 获取序列长度
length = size(states, 2);

ture_trajectory = zeros(3, length);
model_pre_trajectory = zeros(3, length);
EKF_pre_trajectory = zeros(3, length);
P = zeros(3); % 协方差矩阵

x_model_pre = [key_points(:, 1); pi/4]; 
x = [key_points(:, 1); pi/4]; 

%###############################################################################%
% 算法仿真循环
fig = figure;
hold on;
for k = 1:length
    
    % 获取带噪声的控制变量和真实状态以及关键点信息
    Vn = states(k).Vn;
    Gn = states(k).Gn;
    xtrue = states(k).xtrue;
    iwp = states(k).next_keypoint;
    
    % EKF更新预测状态和协方差
    [x, P] = EKF_predict(x, P, Vn, Gn, Q, dt);
    % 获取只由模型预测的姿态
    x_model_pre = vehicle_model(x_model_pre, Vn, Gn, dt);
    
    if states(k).observation_update == 1
        % 获取带噪声的观测
        z = states(k).zn;
        
        % 数据关联
        [zf, idf, zn] = data_associate(x, P, z, R, GATE_REJECT, GATE_AUGMENT); 
        %zf---与地图中已有特征关联的观测
        %zn---认为是新特征的观测
        %idf---与zf关联的索引
        
        % 更新状态向量
        [x, P] = EKF_update(x, P, zf, R, idf); 
    
        % 状态向量增广
        for i = 1:size(zn, 2)
            [x, P] = add_one_z(x, P, zn(:, i), R);
        end
    end
    
    % 清除图像
    cla;
    axis equal
   
    ture_trajectory(:, k) = xtrue(1:3);
    model_pre_trajectory(:, k) = x_model_pre(1:3);
    EKF_pre_trajectory(:, k) = x(1:3);
    
    % 绘制历史轨迹
    plot(ture_trajectory(1, 1:k), ture_trajectory(2, 1:k), 'k--', 'linewidth', 3); % 黑色虚线
    
    % 绘制历史EKF预测轨迹
    plot(EKF_pre_trajectory(1, 1:k), EKF_pre_trajectory(2, 1:k), 'r', 'linewidth', 3); % 红色实线
    
    % 绘制历史模型预测轨迹
    plot(model_pre_trajectory(1, 1:k), model_pre_trajectory(2, 1:k), 'b-.', 'linewidth', 2); % 蓝色点划线
    
    % 绘制地标
    scatter(landmarks(1, :), landmarks(2, :), 'b*');
    
    % 绘制路径点
    plot(wp(1, :), wp(2, :), 'g.', 'markersize', 26);
    
    % 绘制目标点位置
    if iwp ~= 0
        plot(wp(1, iwp), wp(2, iwp), 'bo', 'markersize', 13, 'linewidth', 1);
    end
    
    pause(0.00000001)
end

%###############################################################################%

%---------------------------------FUNCTION-------------------------------------------%

function [G, iwp] = compute_steering(x, wp, iwp, G, rateG, maxG, dt)
    % 检查当前点是否已到达
    cwp = wp(:, iwp); % cwp = wp的第iwp列
    % 计算距离
    d2 = (cwp(1) - x(1))^2 + (cwp(2) - x(2))^2; % 计算当前实际位置与目标点之间的距离

    if d2 < 0.8^2 % 当前实际位置与目标点的距离小于0.8时，判定为已到达
        
        disp(['到达点：', num2str(iwp)]); % 调试信息
        
        % 如果满足距离条件，则进入下一个目的地
        iwp = iwp + 1;
        if iwp > size(wp, 2)
            % 如果循环完成，重置为零
            iwp = 0;
            return;
        end
        % 更新下一个路径点
        cwp = wp(:, iwp);  % cwp = wp的第iwp列，iwp刚刚增加，所以现在cwp存储下一个目标点的坐标
    end

    % 计算新的舵角
    target_angle = atan2(cwp(2)-x(2), cwp(1)-x(1)) - pi/2;
    newG = mod(target_angle - x(3), 2*pi); % 计算从当前车辆方向到目标点的角度差
    i = find(newG > pi);                                                  
    newG(i) = newG(i) - 2*pi;
    i = find(newG < -pi);
    newG(i) = newG(i) + 2*pi;

    % 根据角度差更新转向角G
    if abs(newG - G) > rateG * dt
        newG = G + sign(newG - G) * rateG * dt; % 限制转向角的变化率
    end

    % 限制转向角
    if abs(newG) > maxG
        newG = sign(newG) * maxG;
    end

    G = newG; % 更新舵角
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

function [z,H]= observe_model(x, idf)
%idf - 特征在状态中的索引

Nxv= 3; % 车辆姿态状态数
fpos= Nxv + idf*2 - 1; % xf在状态中的位置
H= zeros(2, length(x));

% 辅助值
dx= x(fpos)  -x(1); 
dy= x(fpos+1)-x(2);
d2= dx^2 + dy^2;
d= sqrt(d2);
xd= dx/d;
yd= dy/d;
xd2= dx/d2;
yd2= dy/d2;

% 预测z
z= [d;
    atan2(dy,dx) - x(3) - pi/2];

% 计算H
H(:,1:3)        = [-xd -yd 0; yd2 -xd2 -1];
H(:,fpos:fpos+1)= [ xd  yd;  -yd2  xd2];

end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

function xv = vehicle_model(xv, V, G, dt)

adjusted_steering = xv(3) + G/2 + pi/2;

% 规范化角度
vangle = mod(xv(3)+ G + pi, 2*pi) - pi;

xv = [xv(1) + V * dt * cos(adjusted_steering); 
      xv(2) + V * dt * sin(adjusted_steering);
      vangle];
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

function [x,P]= EKF_predict (x,P,v,g,Q,dt)

s = sin(x(3) + g/2 + pi/2); 
c = cos(x(3) + g/2 + pi/2);
vts = v * dt * s;
vtc = v * dt * c;

% 计算状态变量的雅可比矩阵
Gv= [1 0 -vts;
     0 1  vtc;
     0 0 1];

% 计算控制变量的雅可比矩阵
Gu= [dt*c -vts;
     dt*s  vtc;
     0 1];
  
% 更新移动机器人的预测协方差矩阵
P(1:3,1:3)= Gv*P(1:3,1:3)*Gv' + Gu*Q*Gu';
% 更新与移动机器人和地标相关的协方差矩阵元素
if size(P,1)>3
    P(1:3,4:end)= Gv*P(1:3,4:end);
    P(4:end,1:3)= P(1:3,4:end)';
end    

% 规范化角度
angle = mod(x(3) + g + pi, 2*pi) - pi;

% 根据模型更新移动机器人的预测姿态
x(1:3)= [x(1) + vtc; 
         x(2) + vts;
         angle];
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [zf,idf, zn]= data_associate(x,P,z,R,GATE_REJECT, GATE_AUGMENT)

zf= []; % 与地图中已有特征关联的观测
zn= []; % 被认为是新特征的观测
idf= []; % 与zf关联的索引

Nxv= 3; % 车辆姿态状态的数量
Nf= (length(x) - Nxv)/2; % 地图中已有的特征数量

% 对最近邻进行线性搜索
for i=1:size(z,2)
    jbest= 0; % 用于存储最佳匹配特征的索引
    nbest= inf; % 用于存储最佳匹配特征的得分（使用马氏距离）
    outer= inf; % 用于存储最低的非门限通过得分
    
    for j=1:Nf
        %计算关联
        [zp,H]= observe_model(x, j);
        v= z(:,i)-zp; 
        
        %v(2) pi2pi
        angle = mod(v(2), 2*pi);
        ti=find(angle>pi);
        angle(ti)=angle(ti)-2*pi;
        ti=find(angle<-pi);
        angle(ti)=angle(ti)+2*pi;
        v(2) = angle;

        % 马氏距离
        S= H*P*H' + R; 
        nis= v'*inv(S)*v;
        nd= nis + log(det(S));
        
        
        if nis < GATE_REJECT && nd < nbest % 如果在门限内，存储最近邻
            nbest= nd;
            jbest= j;
        elseif nis < outer % 否则存储最好的nis值
            outer= nis;
        end
    end
    
    % 将最近邻添加到关联列表中
    if jbest ~= 0
        zf=  [zf  z(:,i)];
        idf= [idf jbest];
    elseif outer > GATE_AUGMENT % z太远而无法关联，但足够远以被认为是新特征
        zn= [zn z(:,i)];
    end
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

function [x,P]= EKF_update(x,P,z,R,idf)

% 检查是否有观测
if size(z,2) == 0
    return; % 如果没有观测，则立即返回
end

lenz = size(z,2); % 观测的数量
lenx = length(x); % 状态向量的长度
H = zeros(2*lenz, lenx); % 初始化观测模型的雅可比矩阵
v = zeros(2*lenz, 1); % 初始化观测残差向量
RR = kron(eye(lenz), R); % 观测噪声协方差矩阵

% 为所有观测构建H矩阵和v向量
for i = 1:lenz
    ii = 2 * i + (-1:0);
    [zp, H_temp] = observe_model(x, idf(i));
    H(ii, :) = H_temp;
    
    angle_residual = mod((z(2, i) - zp(2) + pi), 2 * pi) - pi;
    v(ii) = [z(1, i) - zp(1); angle_residual]; 
end

% 使用乔列斯基分解进行更新
PHt = P*H';
S = H*PHt + RR;
S = (S+S')*0.5; % 确保对称
SChol = chol(S);
SCholInv = inv(SChol); % 三角矩阵
W = PHt * (SCholInv*SCholInv'); % 计算卡尔曼增益
x = x + W*v; % 更新状态
P = P - W*H*P; % 更新协方差

end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

function [x, P] = add_one_z(x, P, z, R) % 用于增广
len = length(x);
r = z(1); % 距离
b = z(2); % 方位

s = sin(x(3) + b + pi/2);
c = cos(x(3) + b + pi/2);

% 用新的地标位置增广x
% 根据调整后的方位计算地标位置
x = [x;
     x(1) + r * c; % 新地标的x位置
     x(2) + r * s]; % 新地标的y位置

% 车辆和测量模型的雅可比矩阵
Gv = [1 0 -r * s;
      0 1  r * c];
Gz = [c -r * s;
      s  r * c];
  
% 增广P：更新新地标的协方差矩阵
rng = len + 1 : len + 2;
P(rng, rng) = Gv * P(1:3, 1:3) * Gv' + Gz * R * Gz'; % 特征协方差
P(rng, 1:3) = Gv * P(1:3, 1:3); % 车辆到特征的交叉相关
P(1:3, rng) = P(rng, 1:3)'; % 特征到车辆的交叉相关
if len > 3
    rnm = 4:len;
    P(rng, rnm) = Gv * P(1:3, rnm); % 地图到特征的交叉相关
    P(rnm, rng) = P(rng, rnm)'; % 特征到地图的交叉相关
end
end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

Matlab仿真结果

实验采用的初始 过程噪声协方差矩阵Q和测量噪声协方差矩阵R如下：

为了进行仿真的对比，我的图像绘制了三条路径：

黑色虚线：不带噪声的真实路径
蓝色长短线：仅由汽车运动模型生成的带噪声路径
红色实线：由EKF-SLAM算法实现的带噪声路径

其他图形：

蓝色‘*’号：随机生成路标的真实坐标
绿色实心圆：汽车的目标点

①初始参数下的表现

首先，使用初始的Q和R运行仿真：

可见，在较低的噪声水平下，EKF路径和模型路径并不能拉开差距，二者都紧密的跟随着真实路径，甚至看不到真实路径的黑线

②噪声水平提高10,000倍下的表现

将噪声提高10000倍并运行仿真：

可见，在噪声水平提高后，EKF和模型路径开始拉开差距，模型路径由于噪声的累计开始偏离路径而EKF依然可以较为准确的跟踪真实路径

③噪声水平提高50,000倍下的表现

将噪声水平进一步提高到50000倍并运行仿真：

可见，在噪声水平再次提高后，模型路径由于强大的噪声累计已经偏离的非常严重，EKF此时也受到了严重的影响，但是依然坚挺

④减少路标下噪声水平提高10,000倍下的表现

最后，为了验证EKF的原理，将路标数量急剧减少，并保持10000倍的噪声水平进行仿真：

可见，在路标很少的情况下，EKF算法也无法有效的规避噪声的累计，和仅靠模型的路径一起偏离真实路径越走越离谱

仿真结论

在landmark数量充足的情况下，EKF-SLAM算法相比单纯的运动模型，可以有效的减少噪声累加带来的影响，显著提升了跟踪的性能

参考

mjmmm

关注

15
点赞
踩
38

收藏

觉得还不错? 一键收藏
2
评论
从零开始使用matlab实现EKF-SLAM算法（含完整代码）

扩展卡尔曼滤波器同步定位与建图 (EKF-SLAM) 算法建立在 EKF 的基础上，集成了 EKF 的功能，可解决机器人技术中最具挑战性的问题之一：同时定位与建图 (SLAM)。 EKF-SLAM采用EKF方法来同时估计机器人的状态和周围环境的布局，而无需事先了解位置。这种双重功能对于在未知环境中运行的自主系统至关重要，使它们能够在绘制区域地图时有效导航。 EKF-SLAM 算法一直是自动驾驶车辆和机器人系统开发的基石，为处理现实世界环境中固有的不确定性提供了一个强大的框架。
复制链接

扫一扫