本文针对交换排序中的快速排序。
快速排序是对冒泡排序的改进。
它引入枢轴的概念,可以任意选key数组中的一个值做枢轴,一般都取key[0],然后分别从高地址到低地址把小的数据放到小的位置;从低地址到高地址把大的数据放到大的位置,经过high-low+1次比较,使得high=low而且high处存放回key[0]数据,这就完成了依次划分(partition)操作,效果是high前的数据不比high处数据大,high后的数据都不比high处数据小,high处的数据就是最终完成时应该放的数据。
然后用递归的方法分别对低子表和高子表进行快速排序。
它的平均时间是knInn,n是记录个数,k是一个常数,而k是同数量级的排序中最小的,所以平均时间比之前的任何排序方法都快。
但是在最坏情况下,即序列已经逆序排放,这样快速排序就会退化成时间复杂度是O(n的平方)。改进的办法就是采用“三者取中法”,取第一个位置、最后一个位置、中间位置的数据中大小适中的那个和第一个位置的数据互换,然后再排,就可以极大改善时间消耗。当然还可以进一步改善的。
在空间上除了2路插入排序需要malloc一个数组外,其他都只需要不超过一个记录的空间;而快速排序需要栈来实现递归,所以在每一次划分后,如果能够取长度短的子序列先快速排序,就能降低栈的深度。
程序:
#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 50
#define N 15
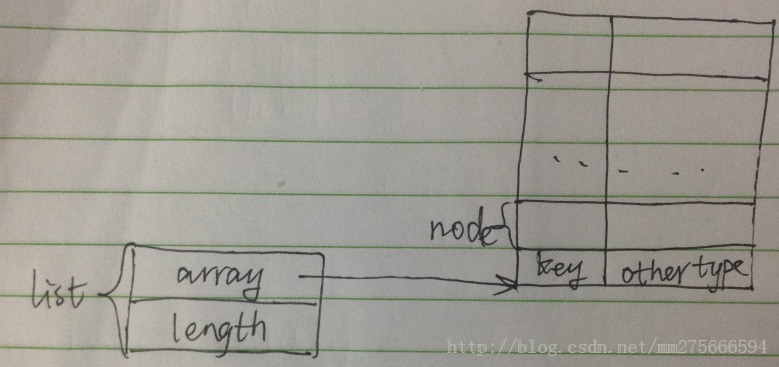
typedef struct{
int key;
int other;
}node;
typedef struct
{
node array[MAXSIZE + 1];
int length;
}list;
//对l->array[low..high]作快速排序
void quicksort(list *l,int low,int high)
{
int pivot;
if(low < high){
pivot = partition(l,low,high);
if((high - pivot) > (pivot > low)){
quicksort(l,low,pivot - 1); //对低子表快速排序
quicksort(l,pivot + 1,high); //对高子表快速排序
}
else{
quicksort(l,pivot + 1,high); //对高子表快速排序
quicksort(l,low,pivot - 1); //对低子表快速排序
}
}
}
int partition(list *l,int low,int high)
{
int pivot;
l->array[0] = l->array[low]; //选枢轴值并备份
pivot = l->array[low].key;
while(low < high){
while(low < high && l->array[high].key >= pivot)
--high;
l->array[low] = l->array[high]; //高位置比枢轴值小的交换到低位置
while(low < high && l->array[low].key <= pivot)
++low;
l->array[high] = l->array[low]; //低位置比枢轴值大的交换到高位置
}
l->array[low] = l->array[0];
return low; //此时low = high
}
//打印序列
void print(list *l)
{
int i;
for(i = 1;i <= l->length;i++)
printf("%d %d\t",l->array[i].key,l->array[i].other);
printf("\n");
}
void main()
{
node data[N]={{5,6},{13,5},{22,2},{2,4},{6,5},{99,7},{6,15},{1,22},{15,12},{58,12},{48,40},{26,48},{38,35},{72,58},{61,22}};
list l;
int i;
for(i = 0;i < N;i++)
l.array[i + 1] = data[i];
l.length = N;
printf("befor sort:\n");
print(&l);
quicksort(&l,1,N);
printf("after quick sort:\n");
print(&l);
}
结果:
[15:25:25]# ./c
befor sort:
5 6 13 5 22 2 2 4 6 5 99 7 6 15 1 22 15 12 58 12 48 40 26 48 38 35 72 58 61 22
after quick sort:
1 22 2 4 5 6 6 15 6 5 13 5 15 12 22 2 26 48 38 35 48 40 58 12 61 22 72 58 99 7

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








