Codeforeces 453A Little Pony and Expected Maximum

A. Little Pony and Expected Maximum

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Twilight Sparkle was playing Ludo with her friends Rainbow Dash, Apple Jack and Flutter Shy. But she kept losing. Having returned to the castle, Twilight Sparkle became interested in the dice that were used in the game.

The dice has m faces: the first face of the dice contains a dot, the second one contains two dots, and so on, the m-th face contains m dots. Twilight Sparkle is sure that when the dice is tossed, each face appears with probability . Also she knows that each toss is independent from others. Help her to calculate the expected maximum number of dots she could get after tossing the dice n times.

Input

A single line contains two integers m and n (1 ≤ m, n ≤ 105).

Output

Output a single real number corresponding to the expected maximum. The answer will be considered correct if its relative or absolute error doesn't exceed 10  - 4.

Sample test(s)

input

6 1

output

3.500000000000

input

6 3

output

4.958333333333

input

2 2

output

1.750000000000

Note

Consider the third test example. If you've made two tosses:

1. You can get 1 in the first toss, and 2 in the second. Maximum equals to 2.
2. You can get 1 in the first toss, and 1 in the second. Maximum equals to 1.
3. You can get 2 in the first toss, and 1 in the second. Maximum equals to 2.
4. You can get 2 in the first toss, and 2 in the second. Maximum equals to 2.

The probability of each outcome is 0.25, that is expectation equals to:

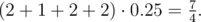
You can read about expectation using the following link: http://en.wikipedia.org/wiki/Expected_value

题意：

一个骰子有M个面，一共抛N次，问选择最大值的期望是多少。

题解：抛N次筛子都有一个一个最大值。有不知道多少种情况。我们可以算出各种M个值的概率再乘上M，求和，即是题目的解。如何求抛N次各个M个值的概率？我们可以动手自己画一下。

共M个面，抛k次。我们求K值的概率(反正最后要除以M^N，先不论)。显然如果第一次抛为K，则随后n-1次抛法随意小于等于K即可，所以概率有K^n-1，随后我们假设第二次抛为K,则我们第一次只能小于K，也就是K-1，否则重复了，随后的n-2次随意小于等于K即可。所以此时概率为(k-1)^1*k^n-2。以此类推，第三次概率为：(k-1)^2*k^n-3.直到n次。我们将其和加起来就是K值的概率。此式明显是等比数列。我们假设最后一项为初始项即为(k-1)^(n-1)。比值为k/(k-1)。我们根据等比数列求和公式可得Sn=a1(1-q^n)/(1-q)=k^n-(k-1)^n。这时将其值除上(M^N)乘上K值就可以算是期望了。当然K要从1枚举到M求和才是最终解。由于当前项与前一项有着千丝万缕的联系，我们可以用递归法求出答案。

#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <iostream>
#include <cmath>
#include <queue>
#include <map>
#include <stack>
#include <list>
#include <vector>
using namespace std;
#define LL __int64
double ksm(double a,int b)
{
	double ans=1;
	while (b!=0)
	{
		if (b & 1)
			ans*=a;
		b>>=1;
		a*=a;
	}
	return ans;
}
int main()
{
	int n,m,i;
	scanf("%d%d",&m,&n);
	double ans=0;
	for (i=1;i<=m;i++)
	{
		double pre=ksm((i-1)*1.0/m,n);
		double now=ksm(i*1.0/m,n);
		ans+=(now-pre)*i;
		pre=now;
	}
	printf("%.12lf\n",ans);
	return 0;
}