【控制理论】#4 稳定性

稳定性的定义

说到稳定性，我们会认为稳定平衡点是稳定的，即当状态变量小范围偏离平衡点时，无论其位于左侧还是右侧，都将随时间回到该平衡点。但在很多情况下，我们无法保证如此严格的稳定，也能容忍一定程度的波动，例如家中的温控系统、抽水马桶的水位等。

李雅普诺夫意义下的稳定性将稳定性的定义延展到了这些稳定性要求较为宽松的情况。为了简化分析，我们以一个平衡点在${\mathbf{z}}_f=0$的二阶系统，则李雅普诺夫稳定性要求平衡点${\mathbf{z}}_f$满足

$$\begin{array}{rl}& \forall t_0,\forall \epsilon >0,\exists \delta (t_0,\epsilon ):\Vert \mathbf{z}(t_0)\Vert <\delta (t_0,\epsilon )\\ \Rightarrow & \forall t⩾t_0,\Vert \mathbf{z}(t)\Vert <\epsilon \end{array}$$

其中，$\epsilon$是人为给定的容忍度，$\delta$是系统根据$\epsilon$确定的初始扰动区。用通俗一点的话讲，对于一个可以容忍的状态变量波动范围，只要系统的初始状态位于平衡点周围的一块初始扰动区内，就可以保证系统的状态变量随着时间增加永远不会超出该容忍范围。可以通过相轨迹更加直观地理解

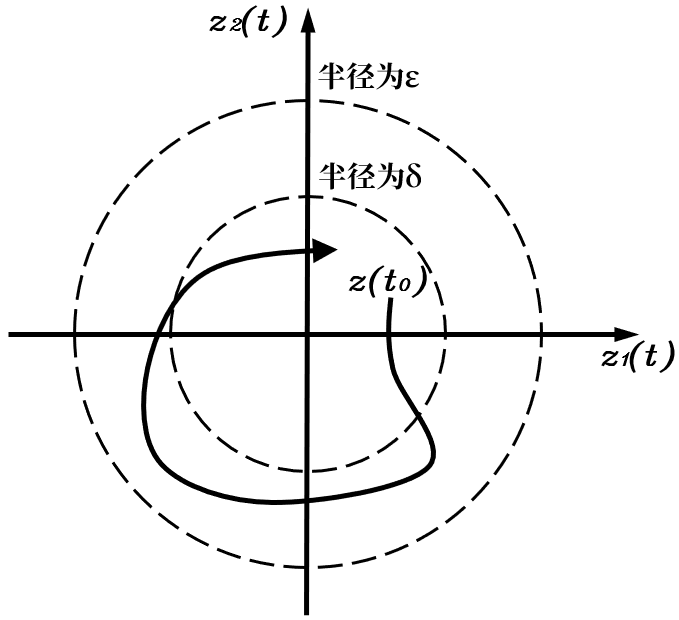
初始扰动区的精确范围并不总是一个圆，使用范数只是为了数学上的严谨和方便，$\delta$更严谨地说是初始扰动区所能容纳的以平衡点为圆心的圆的最大半径，因而会出现划分初始扰动区的圆之外的初始点随时间增加仍然能保持在容忍区内变化的情况。

而一开始所说的状态变量最终收敛于平衡点的情况属于稳定性中的渐进稳定性，即对于平衡点${\mathbf{z}}_f=0$满足

$$\begin{array}{rl}& \exists \delta (t_0)>0:\Vert \mathbf{z}(t_0)\Vert <\delta (t_0)\\ \Rightarrow & \underset{t\to \infty }{\lim }\Vert \mathbf{z}(t)\Vert ={\mathbf{z}}_f=0\end{array}$$

用相轨迹表示为

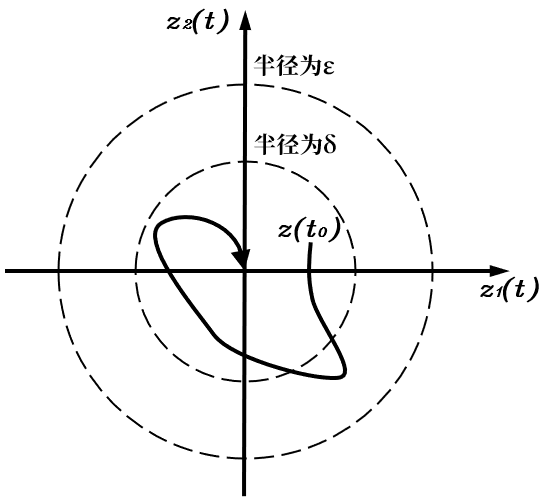
如果平衡点不符合李雅普诺夫稳定性和渐近稳定性，则不稳定。

在满足渐近稳定性的条件下，如果$\delta (t_0)$可以取到无限大，那么就可以推断出平衡点是全局稳定。对于李雅普诺夫稳定性由于$\delta <\epsilon$的条件限制，没有这样的定义，但有一种类似的情况，即系统全局收敛，但并非最终收敛于一个点，而是被控制在一个小的误差范围内，被称作一致最终有界。

稳定性与传递函数

传递函数的极点可以用于判断系统的稳定性。对于一个用传递函数描述的系统

$$X(s)=U(s)G(s)$$

单位冲激响应作为系统最根本的动态特性，是分析稳定性的重要依据。在单位冲激输入下，系统输出的拉普拉斯变换即传递函数本身。在分析传递函数的极点时，其可以写成下面这个形式

$$\begin{array}{rl}X(s)& =G(s)\\ & =\frac{(s-s_{z1})(s-s_{z2})\cdots (s-s_{zm})}{[(s-s_{p1})(s-s_{p2})\cdots (s-s_{pq})][(s-{\sigma }_1\pm \mathrm{j}{\omega }_1)(s-{\sigma }_2\pm \mathrm{j}{\omega }_2)\cdots (s-{\sigma }_r\pm \mathrm{j}{\omega }_r)]}\end{array}$$

其中传递函数$G(s)$包含$m$个零点、$q$个实数根极点和$r$对共轭复数根极点。对其使用分式分解法并进行拉普拉斯逆变换可得

$$x(t)=\sum _{i=1}^q{A}_i{e}^{s_{pi}t}+\sum _{k=1}^r{B}_k{e}^{{\sigma }_{k}t}\sin ({\omega }_{k}t+{\phi }_k)$$

其中$A_i,B_k\ne 0$和${\phi }_k$由传递函数分式分解后各分式的分子得到。

通过上式可以得出以下结论

• 传递函数极点的实数部分$s_{pi}$和${\sigma }_k$将决定系统输出$x(t)$的稳定性：
  • 当所有的$s_{pi},{\sigma }_k<0$时，$x(t)$将随着时间的增加而不断衰减并趋于$0$，满足渐近稳定性。
  • 当至少一个$s_{pi},{\sigma }_k>0$时，$x(t)$将随着时间的增加而发散，系统不稳定。
  • 当所有的$s_{pi},{\sigma }_k⩽0$时：
    • 如果存在${\sigma }_k=0$，$x(t)$将随着时间的增加保持在一个范围内振荡，满足李雅普诺夫稳定性。
    • 否则如果存在$s_{pi}=0$，$x(t)$将随着时间的增加趋于常数，满足渐近稳定性。
• 如果传递函数极点存在虚数部分${\omega }_k$，则系统会产生振荡，只会在实数部分中提到的第三种情况区分系统是渐近稳定还是李雅普诺夫稳定，其他情况不影响系统的稳定性。

在经典控制理论中，稳定特指渐近稳定，李雅普诺夫稳定被称为临界稳定。在这样的定义下，前文讨论的动态系统稳定的条件是传递函数的极点均在复平面的左半部分（不包括虚轴）。

当系统的单位冲激响应满足渐近稳定条件时，针对每一个有界的输入$u(t)$，系统的输出$x(t)$也有界，这种性质被称为有界输入有界输出稳定（BIBO稳定）。如果一个系统不满足BIBO稳定，就意味着一个有限的输入可能会导致无穷幅度的输出，进而可能对系统造成破坏性的影响。

稳定性与状态空间方程

在状态空间方程中，状态矩阵的特征值可以用于判断系统的稳定性。使用状态空间方程描述线性时不变系统的一般表达式为

$$\begin{array}{c}\frac{\mathrm{d}\mathbf{z}(t)}{\mathrm{d}t}=\mathbf{Az}(t)+\mathbf{Bu}(t)\\ \mathbf{y}(t)=\mathbf{Cz}(t)+\mathbf{Du}(t)\end{array}$$

根据前两篇笔记的内容，对于一个二阶系统，在零输入状态下，我们可以总结出状态矩阵$\mathbf{A}$的特征值与稳定性的关系如下表所示

特征值分类	平衡点类型	稳定性分析
均为负数	稳定节点	渐近稳定
一正一负	鞍点	不稳定
均为正数	不稳定节点	不稳定
纯虚数共轭复数	中心点	李雅普诺夫稳定
实大于$0$的共轭复数	不稳定焦点	不稳定
实部小于$0$的共轭复数	稳定焦点	渐近稳定

通过将零状态输入下二维状态变量的平衡点稳定判定方法沿用到更高维度的情况下，我们可以得到关于状态空间方程稳定性的两个结论：

• 如果$\mathbf{A}$的特征值的实部都不大于$0$，它的平衡点将符合李雅普诺夫稳定性。
• 如果$\mathbf{A}$的特征值的实部都小于$0$，它的平衡点将符合渐近稳定性。

研究系统稳定性的判据可以有助于我们明确控制器的设计目标，实现满足稳定性要求的控制系统。