算法通关村——快速排序

深析快速排序

1、快速排序概念

​ 快速排序属于交换排序，通过元素之间的比较和交换位置来达到排序的目的。

​ 快速排序会在每一轮排序中挑选一个基准元素，并让其他比它大的元素移动到数组一边，比它小的元素移动到数组另一边，从而把数组拆解成两部分，如下图所示：

​

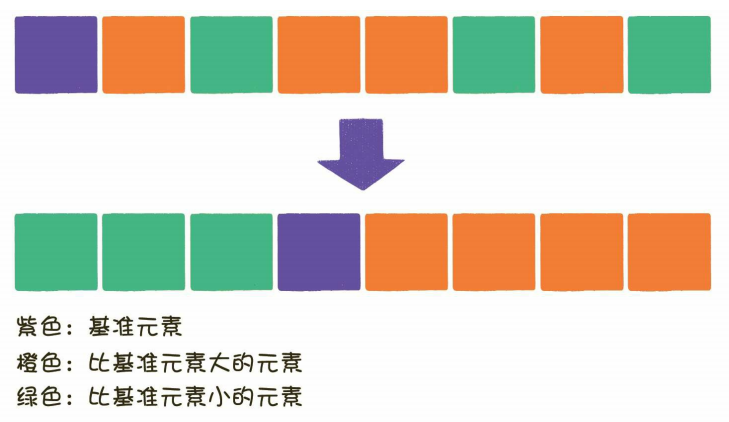
​ 之后再重新在左部分和右部分各自执行快速排序，在将左右两个序列拍好序之后，整个序列就有序了。这里排序进行左右划分的时候是一直划分到子序列只包含一个元素的情况，然后再递归返回。具体的流程如下：

​

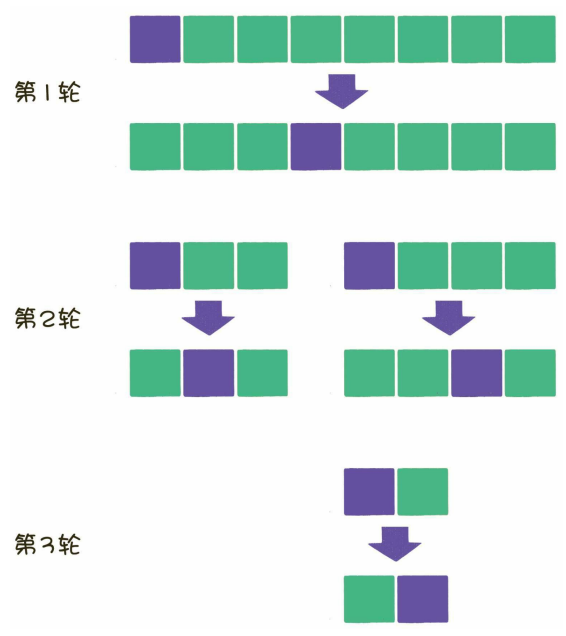
​ 每一轮的比较和交换，需要把数组全部都遍历一遍，时间复杂度是O(n)。假设元素个数是n个，那么平均情况下需要logn轮，因此快速排序算法总体的平均时间复杂度是O(nlogn)。

2、快速排序的代码实现

​ 快速排序的核心框架就是**“二叉树的前序遍历 + 对撞型双指针”**，具体的代码如下：

public static void quickSort(int[] arr, int left, int right) {
    if (left < right) {
        int pivot = arr[right];
        int i = left - 1;
        for (int j = left; j < right; j++) {
            if (arr[j] < pivot) {
                i++;
                int temp = arr[i];
                arr[i] = arr[j];
                arr[j] = temp;
            }
        }
        //哨兵移动到位置pivotIndex上
        int pivotIndex = i + 1;
        int temp = arr[pivotIndex];
        arr[pivotIndex] = arr[right];
        arr[right] = temp;
        
        quickSort(arr, left, pivotIndex - 1);
        quickSort(arr, pivotIndex + 1, right);
    }
}

​ 下面结合具体的一个数组[26, 53, 48, 15, 13, 48, 32, 15]来看一下一次划分的过程。

​

​

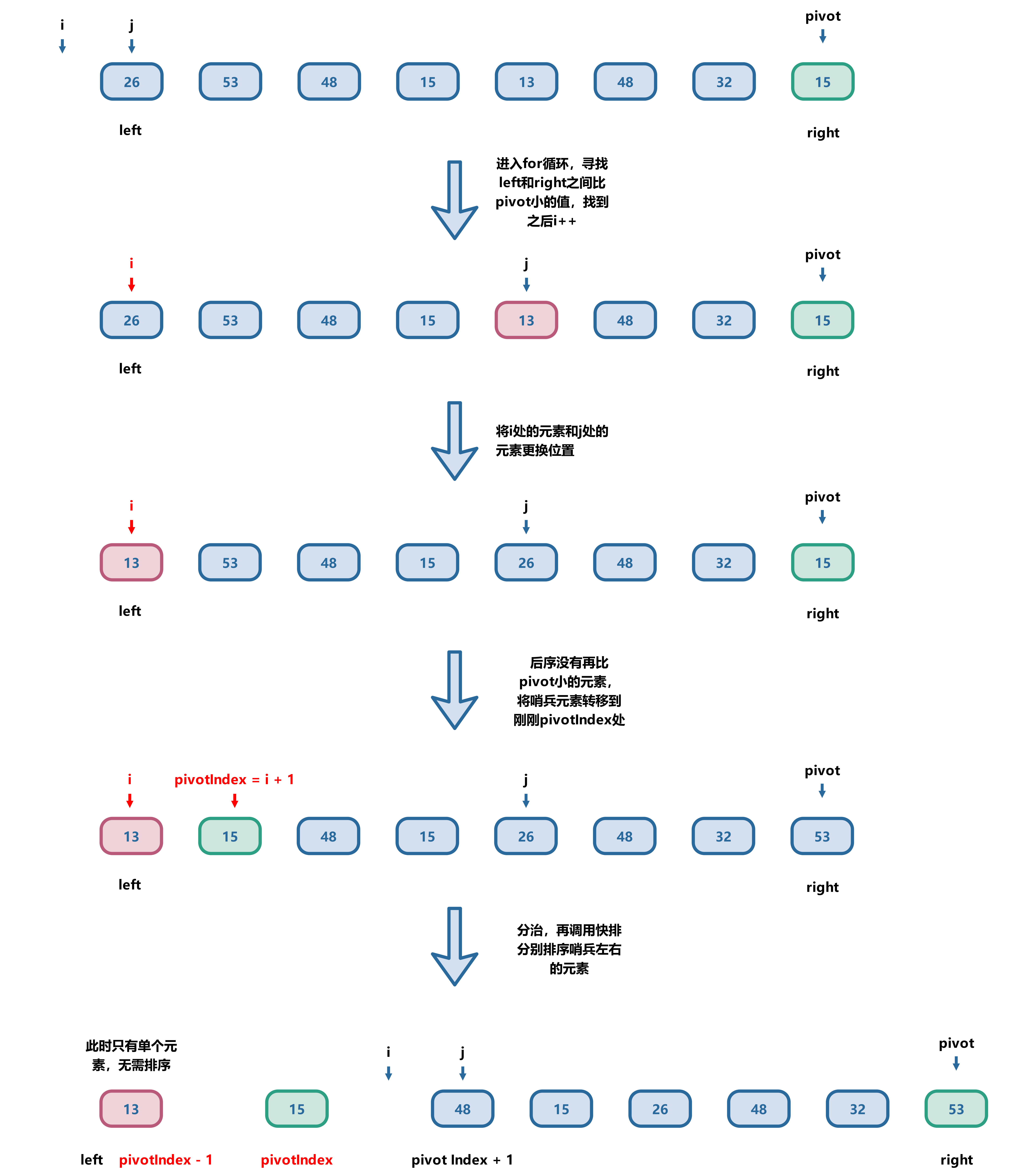
​ 这里i的作用就是负责索引比pivot小的元素，从上图中也可以看到，每发现一个比pivot小的元素，i就加1，同时把该元素调到i的位置，当一次排序结束后，我们可以使pivotIndex = i + 1，再把最开始的pivot对应的arr[right]调换到pivotIndex上，这样pivotIndex左边的元素就都是比pivot小的，右边的元素都是比pivot大的。

​

​ 快排还可以用下面这一种实现：

pubilc static void quickSort(int[] arr, int left, int right) {
    if (start >= end) {
        return;
    }
    //这里就是一个对撞的双指针操作
    int left = start;
    int right = end;
    int pivot = arr[(start + end) / 2];
    
    while (left <= right) {
        //这里是从左边开始找，找到一个比pivot大的元素，然后停下来
        while (left <= right && ar[left] < pivot) {
            left++;
        }
        //这里是从右边开始找，找到一个比pivot小的元素，然后停下来
        while (left <= right && ar[right] > pivot) {
            right--;
        }
        //将刚刚找到的两个元素调换位置，这样比pivot小的元素就在其左边，比他大的在右边
        if (left <= right) {
            int temp = arr[left];
            arr[left] = arr[right];
            arr[right] = temp;
            //调换完位置后继续往中间找
            left++;
            right--;
        }
        //直到left > right，这时pivot左边的元素都是比它小的，pivot右边的元素都是比它大的
    }
    
    //先处理元素再分别递归两侧分支，与二叉树的前序遍历非常像
    quickSort(arr, start, right);
    quickSort(arr, left, end);
}

3、复杂度分析

​ 快速排序的时间复杂度计算比较麻烦。从原理来看，如果我们选择的pivot每次都在正中间，效率是最高的，但是这是无法保证的，因此我们需要从最好、最坏的中间情况分析

• 最坏情况就是如果每次选择的恰好都是low节点作为pivot，如果元素恰好都是逆序的，此时时间复杂度为$O(n^2)$

• 如果元素刚好是有序的，则时间复杂度为$O(n)$

• 这种的情况是每次选择的都是中间节点，此时序列每次都是长度相等的序列，此时时间复杂度为$O(nlo{g}_{2}n)$