prufer数列学习笔记

学了一种新姿势叫prufer数列，可以用来解一些关于无根树计数的问题。

prufer数列是一种无根树的编码表示，对于一棵n个节点带编号的无根树，对应唯一一串长度为n-2的prufer编码。

（1）无根树转化为prufer序列。

首先定义无根树中度数为1的节点是叶子节点。

找到编号最小的叶子并删除，序列中添加与之相连的节点编号，重复执行直到只剩下2个节点。

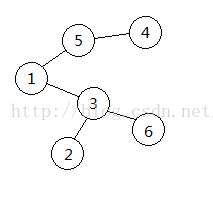
如下图的树对应的prufer序列就是3，5，1，3。

具体实现可以用一个set搞定，维护度数为1的节点。复杂度O(nlgn)。

/**********************
给一棵无根树进行prufer编码
**********************/

#include <iostream>
#include <cmath>
#include <cstdlib>
#include <time.h>
#include <vector>
#include <cstdio>
#include <cstring>
#include <set>
using namespace std;
#define maxn 1111111
#define maxm 2111111

set <int> gg;
struct node {
	int u, v, next;
} edge[maxm];
int n, head[maxn], cnt, degree[maxn];
bool vis[maxn];

void add_edge (int u, int v) {
	edge[cnt].u = u, edge[cnt].v = v, edge[cnt].next = head[u], head[u] = cnt++;
}

int main () {
	cin >> n;
	memset (head, -1, sizeof head);
	memset (degree, 0, sizeof degree);
	memset (vis, 0, sizeof vis);
	gg.clear ();
	cnt = 0;
	for (int i = 1; i < n; i++) {
		int u, v;
		scanf ("%d%d", &u, &v);
		add_edge (u, v);
		add_edge (v, u);
		degree[u]++, degree[v]++;
	}
	for (int i = 1; i <= n; i++) {
		if (degree[i] == 1) {
			gg.insert (i);
			vis[i] = 1;
		}
	}

	set<int>::iterator it;
	int prufer[maxn], id = 0;
	for (; id <= n-3;) {
		int u = (*(it = gg.begin ()));
		gg.erase (u);
		for (int i = head[u]; i != -1; i = edge[i].next) {
			int v = edge[i].v;
			if (vis[v])
				continue;
			degree[v]--;
			prufer[++id] = v;
			if (degree[v] == 1) {
				gg.insert (v);
				vis[v] = 1;
			}
		}
	}
	for (int i = 1; i <= id; i++) {
		cout << prufer[i] << " ";
	} cout << endl;
	return 0;
}

（2）prufer序列转化为无根树。

设点集V={1,2,3,...,n}，每次取出prufer序列中最前面的元素u，在V中找到编号最小的没有在prufer序列中出现的元素v，给u，v连边然后分别删除，最后在V中剩下两个节点，给它们连边。最终得到的就是无根树。

具体实现也可以用一个set，维护prufer序列中没有出现的编号。复杂度O(nlgn)。

/**********************
prufer序列解码
**********************/

#include <iostream>
#include <cmath>
#include <cstdlib>
#include <time.h>
#include <vector>
#include <cstdio>
#include <cstring>
#include <set>
using namespace std;
#define maxn 1111111
#define maxm 2111111

int n;
int prufer[maxn], node[maxn], cnt;
set<int> gg; //在prufer序列里没有出现的点
int vis[maxn]; //这个点是不是在prufer序列里面
bool used[maxn]; //这个点有没有使用过

int main () {
	cin >> n;
	gg.clear ();
	memset (vis, 0, sizeof vis);
	memset (used, 0, sizeof used);
	cnt = 0;
	for (int i = 1; i <= n-2; i++) {
		cin >> prufer[i];
		vis[prufer[i]]++;
	}
	for (int i = 1; i <= n; i++) {
		if (!vis[i]) {
			gg.insert (i);
		}
	}
	set<int>::iterator it;
	for (int i = 1; i <= n-2; i++) {
		int v = (*(it = gg.begin ())), u = prufer[i];
		cout << u << "-" << v << endl;
		used[v] = 1;
		gg.erase (v);
		vis[u]--;
		if (!vis[u] && !used[u]) {
			gg.insert (u);
		}
	}
	it = gg.begin ();
	cout << *it << "-" << *(++it) << endl;
	return 0;
}

最后有一个很重要的性质就是prufer序列中某个编号出现的次数+1就等于这个编号的节点在无根树中的度数。