（ECCV 2022）E-NeRV: Expedite Neural Video Representation with Disentangled Spatial-Temporal Context-CSDN博客

E-NeRV: Expedite Neural Video Representation with Disentangled Spatial-Temporal Context （ECCV 2022）

Paper：https://arxiv.org/abs/2207.08132
Code:https://github.com/kyleleey/E-NeRV

Abstract

最近，视频的图像级隐式神经表示(NeRV)因其与常规的像素级隐式表示相比具有良好的结果和快速的速度而受到欢迎。然而，当扩展到理想的性能时网络结构中的冗余参数可能会导致模型规模较大。造成这一现象的关键原因是NeRV的耦合表述，它直接从帧索引输入中输出视频帧的时空信息。在本文中，我们提出了E-NeRV，它通过将图像隐式神经表示分解到独立的空间和时间上下文中，显著地加快了NeRV。在新公式的指导下，我们的模型在保留表示能力的同时，大大减少了模型参数的冗余。我们通过实验发现，我们的方法可以在更少的参数下，在很大程度上提高性能，从而使收敛速度提高了8倍以上。

1. Introduction

隐式神经表示(INR)近年来越来越流行。它提出了一种表示连续信号的新方法 $f_\theta:\R^m \to \R^n$ ，将信号属性编码为一个函数，该函数将 $m$ 维输入(如坐标)映射到期望的 $n$ 维输出(如RGB值、占用率、密度)，并通过带有权重 $θ$ 的深度神经网络参数化该函数。与常规的网格化表示不同，紧凑的INRs被证明适用于复杂场景和任意尺度采样，以及大量3D任务和图像表示。尽管INR普遍存在，但对视频信号兼容INR的研究却很少。

在过去的INR工作中，视频被视为图像的额外补充。他们通常采用三维时空坐标 $(x, y, t)$ 作为输入并输出RGB值。以下大部分关注视频INRs的工作[41,63]采用这种配置。然而，当处理分辨率大、帧数多的视频序列时，这种类型的视频INR的训练和推理速度将提高3次方次。相比之下，最近提出的NeRV[2]方法将视频信号的INR重新表示为 $f_\theta: R→R^{3×H×W}$ 。基于视频是图像片的概念，NeRV提出了一种不同于其他像素级视频INR的图像级视频INR。NeRV以时间轴上的帧索引作为输入，直接输出所需的帧图像。在NeRV[2]中，实验证明训练和推理速度比以前的方法快得多。NeRV结合了卷积结构的成功和GAN的网络设计为它的NeRV块，赋予了重构大分辨率和高保真帧的能力。通过改变NeRV块中的通道尺寸，我们可以得到一系列不同尺寸的NeRV模型(参数越多的NeRV模型自然表现更好)。然而，随着通道尺寸的增大，模型尺寸会迅速增大。这个缺点主要来自于NeRV模型的架构，它带来了大量不必要和冗余的参数(当通道尺寸增加25%时，模型尺寸增大2倍)。我们将其归因于NeRV的设计动机:NeRV以混合的方式考虑每一帧图像中的空间和时间信息，并直接从一个特定的时间帧索引生成，这导致了沉重的模型和次优性能。
在这里插入图片描述

受视频GAN研究将内容和运动信息进行分解的启发，我们提出了图像级视频INR，其可以显式地分离时空背景，并将它们融合在一起进行最终预测，重构了原始NeRVe网络架构。基于这一动机(如图1所示)，我们可以有效地降低基线模型的参数大小(从12M到5M)，同时保持大部分性能。我们进一步在卷积块中引入时间嵌入，以提高表示能力。此外，我们发现了NeRV块中多余的设计并改进它。我们将我们的方法命名为E-NeRV，因为它从视频隐式表示的解纠缠角度加速了原始NeRV。我们系统地研究了多种设计选择，并将我们的方法与基线NeRV模型进行了比较。我们的贡献总结如下:

我们确定了图像级视频INR-NeRV中的冗余结构，这是它在放大以获得更好性能时的主要限制，并将此缺点归因于它的混合方式。
我们提出了一种新的时空背景分离的图像视频隐式神经表示E-NeRV。
我们证明了我们的方法在收敛速度(8×)和较少参数的情况下，始终优于NeRV基线。此外，不同的视频INR下游应用之间的优越性能是一致的。

2. Related Work

2.1 Implicit Neural Representation

近年来，隐式神经表示(INR)以其对多种信号建模的强大能力而受到广泛的关注。它通过一个函数来参数化一个特定的信号，该函数输出所提供的坐标类输入的所需属性，并使用深度神经网络(通常是多层感知器，MLP)来近似该函数。因此，信号隐式编码在网络参数中。例如，图像[6,27,43]可以定义为每个像素位置的RGB值，3D物体或场景可以表示为每个3D点的占用率[29,38]、有符号距离[35]或亮度场[30]。INRs主要用于3D视觉任务，如重建和新视图合成。

在这一趋势下，视频的隐性表征并没有得到深入的研究。常规视频隐式表示通常以像素的时空索引 $x, y, t)∈\R^3$ 为输入输出特定像素在特定帧内的RGB值。这种简单的定义适合图像尺寸较小的短视频剪辑，如[43,27]中的7 × 224 × 224。[41]进一步估计了连续视频表示的光流。但这种设置已经不适合大尺度图像分辨率数百帧的视频，由于帧数和像素的增加，需要很长时间进行优化和推理[2]。此外，[27]中提出的用于上下文嵌入的范例也不能支持具有大量帧数的视频。视频INRs的另一个研究方向是生成对狂网络。DiGAN[62]不是直接从潜码生成视频，而是从上下文和运动潜码生成视频INRs参数。StyleGAN-V[44]进一步利用卷积算子进行大规模图像合成。然而，在这项工作中，我们专注于将INR拟合到特定的视频，而不是在基于GAN的方法中生成不同的内容。

最近提出的NeRV[2]对视频采用了图像级隐式表示，而不是以前的像素式表示。通过将隐式表示与卷积的进步相结合进行图像合成，NeRV以更少的训练和推理时间获得了有前景的结果。NeRV之后,我们
E-NeRV通过解纠缠公式进一步改进了架构，获得了优越的性能和快速收敛。

2.2 Optimization of INRs

尽管INRs的表达能力获得了成功，但它们自然需要很长时间来优化以获得可观的性能。人们提出了许多方法来缓解这一问题，并获得更好的表示能力。

从函数特性的角度来看，研究可分为研究最优编码方法和应用网络正则化。 考虑到INRs倾向于在高维网络输入下学习更好的映射函数，许多后续工作都专注于更好的编码方法。考虑到INRs倾向于在高维网络输入下学习更好的映射函数，许多后续工作都专注于更好的编码方法。径向基函数(RBF)[7]利用嵌入RBF编码的加权和。在傅立叶特征网络(FFN)[47]中提出的位置编码(PE)使用一组傅立叶函数将输入投影到高维上，后续的工作[21,13]在频率上采用从粗到细的策略，以获得更好的收敛性。与使用现有函数不同，SPE[53]使用可学习样条函数，最新的instant-ngp[31]为共享嵌入空间构造了可训练的哈希映射。关于正则化，在视图合成中已经研究了许多关于3D属性的一致性约束[16,8,32]。文献[46]通过元学习方法对域内初始化进行正则化。基于分布的[40]和基于lipschitz的[23]正则化可应用于MLP的光滑先验，以获得更好的收敛性和泛化性。

从网络体系结构的角度来看，最近的一些工作旨在通过针对三维稀疏性的精心设计的体系结构来加速三维INRs的训练和/或推理。一种常用的方法是将MLP的特征存储在预定义的体素空间[23]、点云[58]或八叉树结构[60]中，从而减少训练和推理中点查询的次数。在更大的范围内，SIREN[43]用正弦激活函数取代了现有mlp中常用的RELU激活，并显示出对复杂信号的坚实拟合能力。ACORN[26]和CoordX[20]旨在通过不同的方法减少基于坐标的模型的查询数量: ACORN[26]采用分层的方式对多尺度坐标进行分解而CoordX[20]设计了一个分割的MLP架构，以利用输入坐标点之间的局部性。下面的MINER[42]通过跨尺度相似先验改进了ACORN。

我们的工作从架构的角度加速了NeRV，因为我们观察了现有的不必要和冗余的结构。通过引入我们的解纠缠公式，我们证明了具有更少参数的结果模型可以保持大部分性能，甚至超过NeRV基线。当扩展到与基线NeRV模型相同的尺寸时，我们的E-NeRV显示出更好的性能和更快的收敛速度。

3. Preliminaries

NeRV是一种图像级表示方法，通过映射函数 $f_θ : \R → \R^{3×H×W}$ 表达视频信号，映射函数由网络权重 $\theta$ 参数化得到。给定一个包含 $T$ 帧的视频 $V= \{v_t\}_{t=1}^T$ ，输入是一个标准化为 $t \in [0, 1]$ 的标量帧索引值，输出是整幅相应的帧图像 $v_t \in \R^{3 \times H \times W}$ 。通过仔细观察它的架构，这个公式可以分为两个部分:
在这里插入图片描述
其中 $γ (t)$ 表示[30]中提出的规则频率位置编码:

其中 $b$ 和 $l$ 是超参数。函数F代表MLP结构，G代表卷积生成器。更具体地说，它包含了一系列具有卷积和pixelshuffle层的NeRV块，用于上采样和图像生成。网络首先将输入帧索引的位置编码映射为一维特征向量，然后将该向量重塑为二维特征映射 $f_t∈\R^{C×h×w}$ ，在NeRV设置中 $(h, w) = (9, 16)$ 。接下来的卷积和Pixelshuffle操作将特征图逐渐变换为原始图像大小。 $1 \times 1$ 卷积与 $s i g m o i d$ 激活生成所需的三通道归一化RGB值。

NeRV的成功有几个原因。它采用了一种基于图像的表示，避免了逐像素训练和推理。文献[2]中的定量比较显示出与按像素表示相比，训练和推理速度有很大的提高。包含卷积和像素-shuffle的NeRV块适用于图像生成，最终性能的PSNR约为40，优于其他视频隐式神经表示。

[2]中提供了一系列不同尺寸和性能的模型。一个更大的模型可以获得更好的性能，以及模型放大的方法是增加NeRV块内的通道尺寸。然而，这种模式仍然存在缺陷。第一个问题是MLP的最后一层。为了生成特征向量能够重构为 $\times h \times w$ 的特征图。MLP的最后一层是特别宽的，一些简单的解决方案将导致很大的性能下降(详见第5.4节)。 然后，由于下面的大尺度因子Pixelshuffle层，卷积核也可以是巨大的。

NeRV将图像级视频隐式表示看作一个索引到图像的范式，而我们认为它是一个表述解纠缠的生成过程，框架索引只代表时间上下文。在第4节中，我们阐述了我们用时空解纠缠升级冗余结构的尝试，并在第5节中定量和定性地展示了我们方法的显著性能和收敛速度。

4. Methodology

所提出的E-NeRV的总体架构如图2所示。本节将介绍我们处理冗余参数和结构的方法。更具体地说，在4.1节中，我们阐述了如何分离空间和时间表示以及由此产生的公式和结构。而在第4.2节阐述了我们对NeRV块的升级设计。
在这里插入图片描述

4.1 Disentangled image-wise video INR

NeRV的第一个冗余部分出现在MLP的最后一层。例如，具有12.5M参数的NeRV-L模型，百分之七十的参数来自于最后一个MLP层，其输出为 $f_t \in 112 \times 9 \times 16$ 。虽然特征图的高度和宽度都比较小，但它需要大量的通道数来保证最终的性能。在实验中(第5.4节)，我们展示了一些小的修改，这些修改可能会缓解较大的参数，但与我们的相比会导致显著的性能下降。我们认为这个结构是必须存在的，因为NeRV只从输入 $t$ 直接生成帧特征图 $f_t$ ，同时这意味着从时间输入中同时得到空间和时间信息。

作为一种替代方法，我们建议将时空信息进行分离，让时间输入成为对空间空间进行操作的特征向量。具体来说，我们将 $f_t$ 的生成重新表述为:
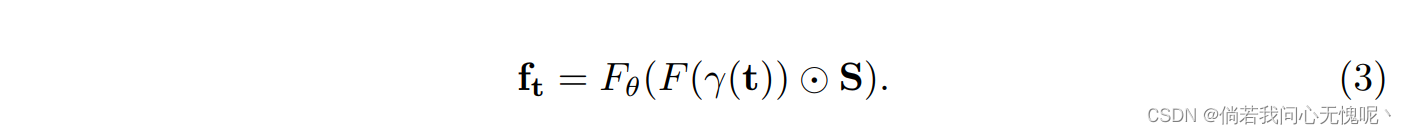
在这里插入图片描述
这里F仍然代表MLP网络，但参数尺寸小得多，因为在我们的方法中F的输出只是d维向量，其中 $\ll C × h × w$ 。我们将时空信息分解成编码为 $F (γ (t))$ 的时空信息，和编码在空间上下文嵌入 $S∈\R^{d×h×w}$ 中的空间域。然后利用 $F_θ$ 轻量网络将分离的时空信息融合到时空嵌入中。

由于 $S$ 被期望包含空间上下文，我们使用规范化的网格坐标初始化它。因此我们得到了初始化的空间上下文 $S_0∈R^{2 \times h×w}$ 。首先，我们使用类似于Eq. 2中的频率位置编码 $γ (\cdot)$ 将 $S_0$ 编码为 $\hat{S_0}$ 。然后，我们在这里采用单头自注意和残差连接的小型变Transformer[49]，鼓励空间位置之间的特征融合，得到空间上下文 $S$ :
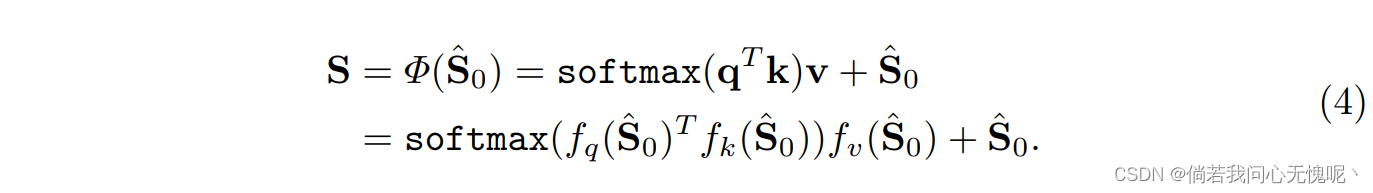
在这里插入图片描述

~~***这是Transformer的一个小公式***~~

其中 $f_{\ast}$ 表示不同的投影网络，将输入特征图的通道维度投影到所需的维度 $d_t$ 。其中 $q, k, v$ 表示Transformer中的查询，键和值。现在可以将 $S$ 视为包含所需空间上下文的嵌入。在表示不同的视频时， $Φ$ 中的可学习参数是不同的。换句话说，我们用 $Φ$ 的权重参数化视频中的空间信息。

接下来，在解纠缠过程完成后，我们需要将时间向量 $F(γ(t))∈\R^d$ 与空间上下文 $S∈\R^{d×h×w}$ 进行融合，得到时空信息。首先，我们将时间向量与 $S$ 中所有位置的每个特征向量按元素顺序相乘，然后利用 $F_θ$ 进一步将特征融合在一起。这里的 $F_θ$ 可以是任何操作，只要它能鼓励空间和通道特征融合。我们使用了一个类似 $Φ$ 的微型多头注意转换器网络，它具有远程建模和特征融合的能力。在实验中，我们进一步将这种选择与其他选择进行比较(第5.4节)。

此外，我们观察到NeRV中的时间信息只与公式1中函数G开始处的特征映射有关。因此，我们进一步将时间上下文融合到G中的每个NeRV block中，使时间嵌入得到充分和彻底的利用。在实验中，我们发现这种设计可以进一步提高性能。具体而言，我们从GAN[15]的设计中获得灵感，并将时间语境作为风格向量的概念。不同于用元素乘法得到粗略的时空特征图，这里的时间信息只起到分布位移的作用。

如图2上半部分所示，我们使用一个小型MLP用于生成时间特性 $l_t \in \R^{d_0}$ 。然后对于第 $i$ 块 $(i = 1 ， \dots 5)$ ，线性层 $M_i$ 产生全通道平均 $µ_i$ 和相应的标准偏差 $σ_i$ 。我们将第 $i$ 块的输入特征映射表示为 $f_t^i$ 。这个新生成的分布将特征映射转换为具有时间上下文的实例规范化:
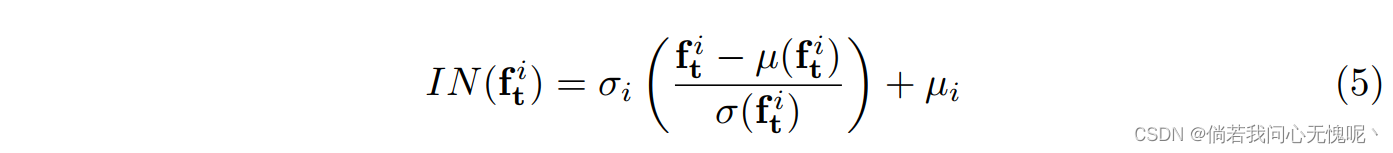
在这里插入图片描述
其中 $µ(f_t^i)$ 和 $σ(f_t^i)$ 是跨空间维度计算的。这个操作在每个块的开始进行，让时间信息引导相应帧的生成。

4.2 Upgraded NeRV Block

如第3节所述，另一个冗余结构位于NeRV块中。由于卷积需要生成足够的通道进行进一步的pixel shuffle操作，如果输入特征映射的信道维数为 $C_1$ ，期望输出尺寸为 $C_2$ ，上样本比例因子为 $s$ ，核大小为 $3 \times 3$ ,不考虑偏差，则需要训练的权重大小为 $C_1 × C_2 × s × s × 3 × 3$ 。当比例因子s较大时，例如，第一个NeRV块中的s = 5，如果我们扩大输入和输出通道维度以获得更好的性能，则尺寸可能非常大(高达整个模型的65%)。

为了解决这个问题，我们用一个微妙的设计修改了NeRV块:我们用连续两个带有小通道的卷积来代替原始卷积核。然后我们将像素洗牌操作放在中间，并引入一个中间维度 $C_0$ 。用 $co n v (\cdot ， \cdot)$ 表示具有相应输入输出通道尺寸的卷积核，我们的新架构可以表示为：
在这里插入图片描述
新公式中的参数为: $3 × 3 × C_0 × (C_1 × s × s + C_2)$ 。实践中，我们将 $C_0$ 设为 $min(C_1,C_2)/4$ 。如果 $C_1 \le C_2$ ，参数大小之比为 $(C_1/4C_2 + 1/4s^2) \approx C_1/4C_2 \leq 1/4$ 。我们发现替换了第一个NeRV采用这种设计的块可以极大地简化尺寸，同时保持大部分性能(参见第5.2节)。原因是第一个块的比例因子等于5，从而导致了一个超大的模型。下面因子等于2的块不会从这个修改中受益太多，所以在我们的最终设置中，我们用升级的版本替换第一个NeRV块。

5. Experiments

5.1 Datasets and Implementation Details

我们对从scikit-video和UVG[28]数据集中收集的8个不同的视频序列进行了定量和定性的比较实验，类似于NeRV中的实验室。每个视频序列约150帧，分辨率为1280 × 720。我们对模型的每个块设置上比例因子5、2、2、2、2，从大小为16 × 9的特征图重构出1280 × 720的图像。为了进行公平的比较，我们遵循原始NeRV实现的训练计划。我们使用Adam优化器[17]训练模型。除指定外，每个模型在每个视频序列上训练300个epoch，批处理大小为1。

我们采用参数为12.57M的NeRV-L作为基线。对于模型中与我们的修改不想关的部分，我们遵循与NeRV中相同的设置，比如激活选择。我们设置 $d = d_t = 256$ 用于空间和时间特征融合， $d_0 = 128$ 用于时间实例归一化。我们将模型中的所有位置编码层设置为与公式2中表述的NeRV的位置编码相同，并使用b = 1.25和l = 80(如果没有另外表示)。对于训练目标，我们使用与[2]相同的L1和SSIM损失组合。
在这里插入图片描述
其中 $\alpha$ 设置为0.7，T表示视频帧的总体数量， $v_t$ 表示重建的帧图像并且 $\hat{v_t}$ 表示相应的地面真值。请参考补充材料，以获得更多的实现细节，实验，结果和可视化。

5.2 Process of Removing Redundan Part and Scalling Up

在本节中，我们展示了如何用我们提出的方法替换冗余的结构和参数，并在卷积阶段逐步将保存的参数分配到通道中，最终得到参数更少但性能更好的E-NeRV。

整个过程如图3所示。我们首先用方程3中解纠缠的公式和相应的结构替换重的MLP。这一步可以将参数从12.57M降低到5.5M，而得到的模型仍然可以得到38.04的PSNR。相比之下，[2]中参数较多的神经网络- m模型只能达到36.05 PSNR的较差性能。然后，我们先将卷积块中的通道进行缩放，得到一个尺寸类似于NeRV-L的模型，缩放后的模型可以得到41.70的PSNR。
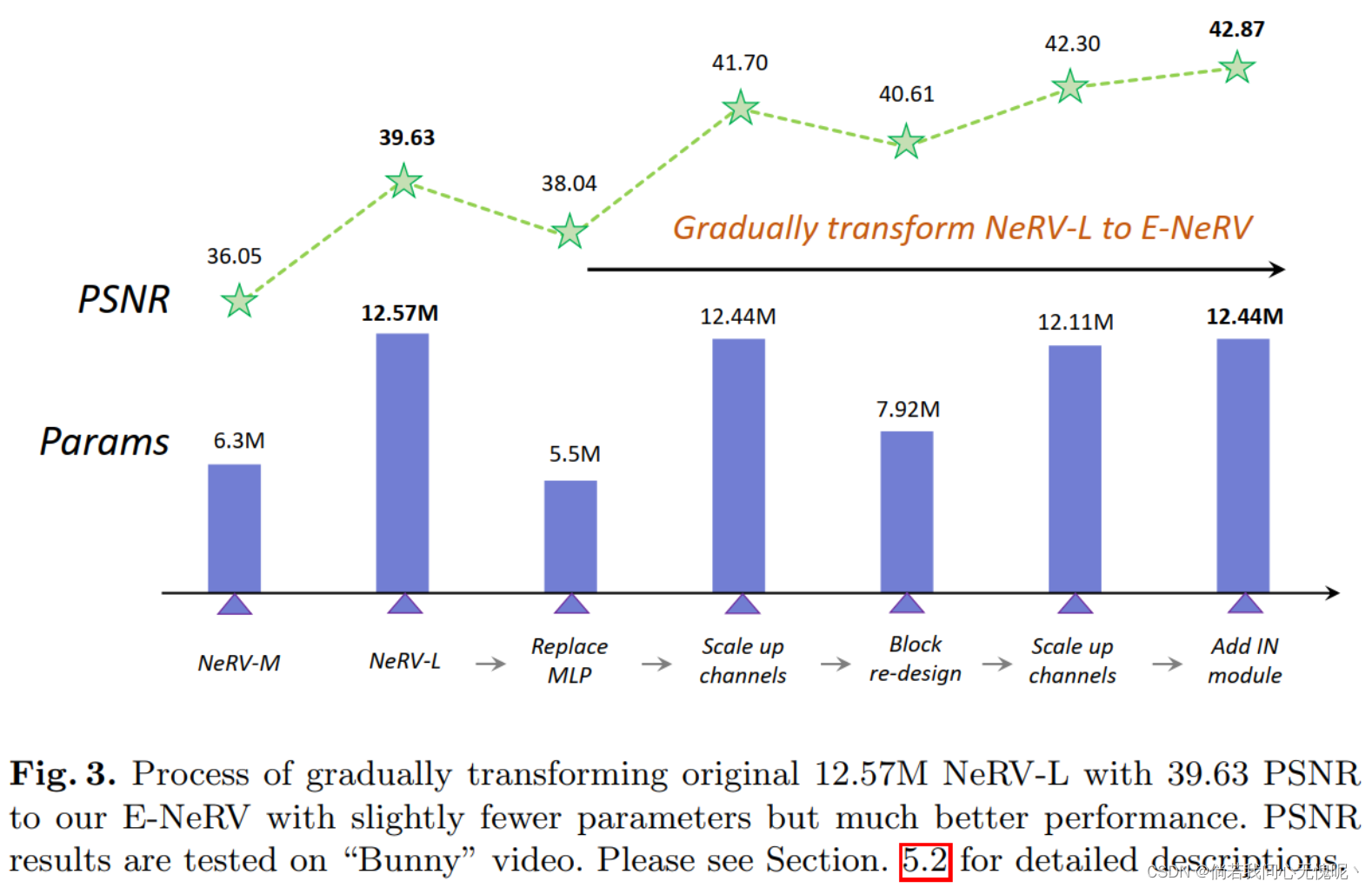
在这里插入图片描述
在第一次缩放之后，另一个冗余结构出现了:具有5倍缩放因子和大通道尺寸的NeRV Block可能会令人难以承受，所以我们用我们的新设计替换它。如图3所示，得到的模型减少了37%的参数。值得注意的是，与原始NeRV-L相比，得到的模型已经有更少的参数(7.92M vs. 12.57M)，但性能更好(40.61M vs. 39.63M)。然后，我们再次扩大通道，最后为我们提出的E-NeRV添加时间实例归一化分支。

5.3 Main Results

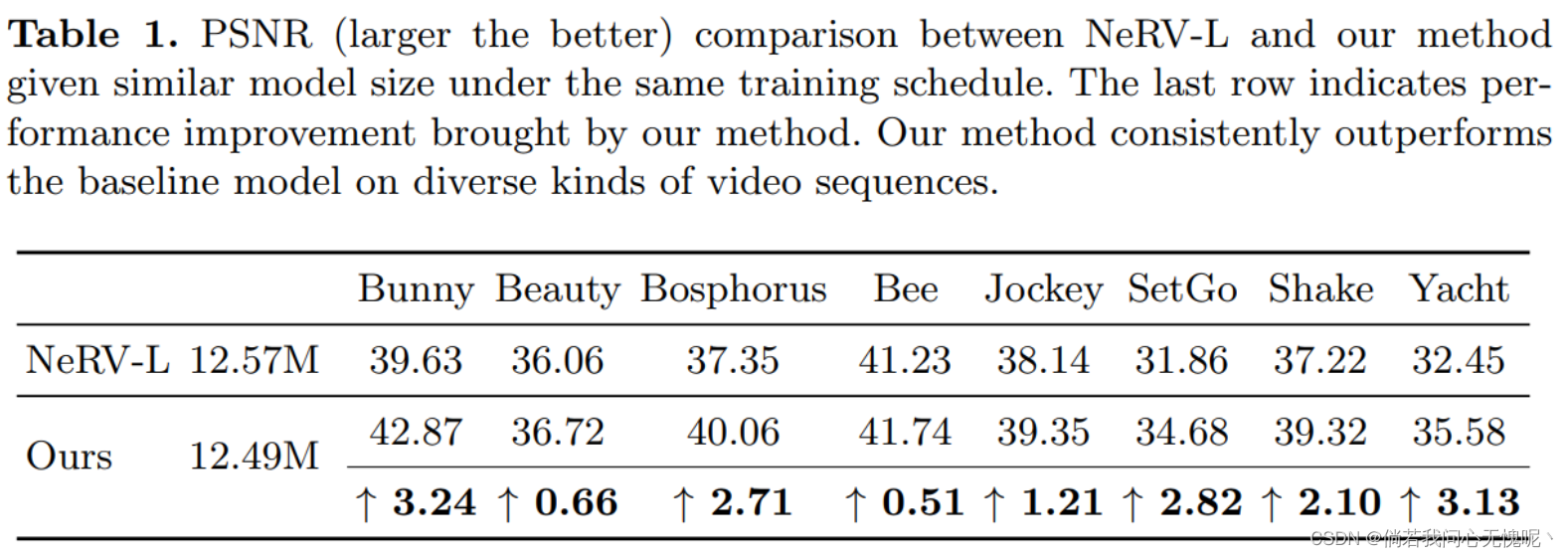
我们在表1中提供了我们的方法和NeRV的比较。我们参考[2]与像SIREN[43]和FFN[30]这样的基于像素的视频INRs进行进一步的比较，这表明NeRV在性能和速度上都超过了这些方法。虽然我们提出的E-NeRV具有相似的速度和参数，但在不同的视频序列上，它始终比NeRV表现更好。

因为我们提出的E-NeRV的设计不使用任何类型的先验数据，我们声称这种改进存在于使用E-NeRV来表示任何视频序列时。值得注意的是，我们的方法可以为表1中内容更动态的视频带来更大的提升，例如“兔子”和“游艇”视频。我们认为这是因为我们的解纠缠隐式表示可以更好地模拟具有更多动态内容的视频的空间和时间变化。
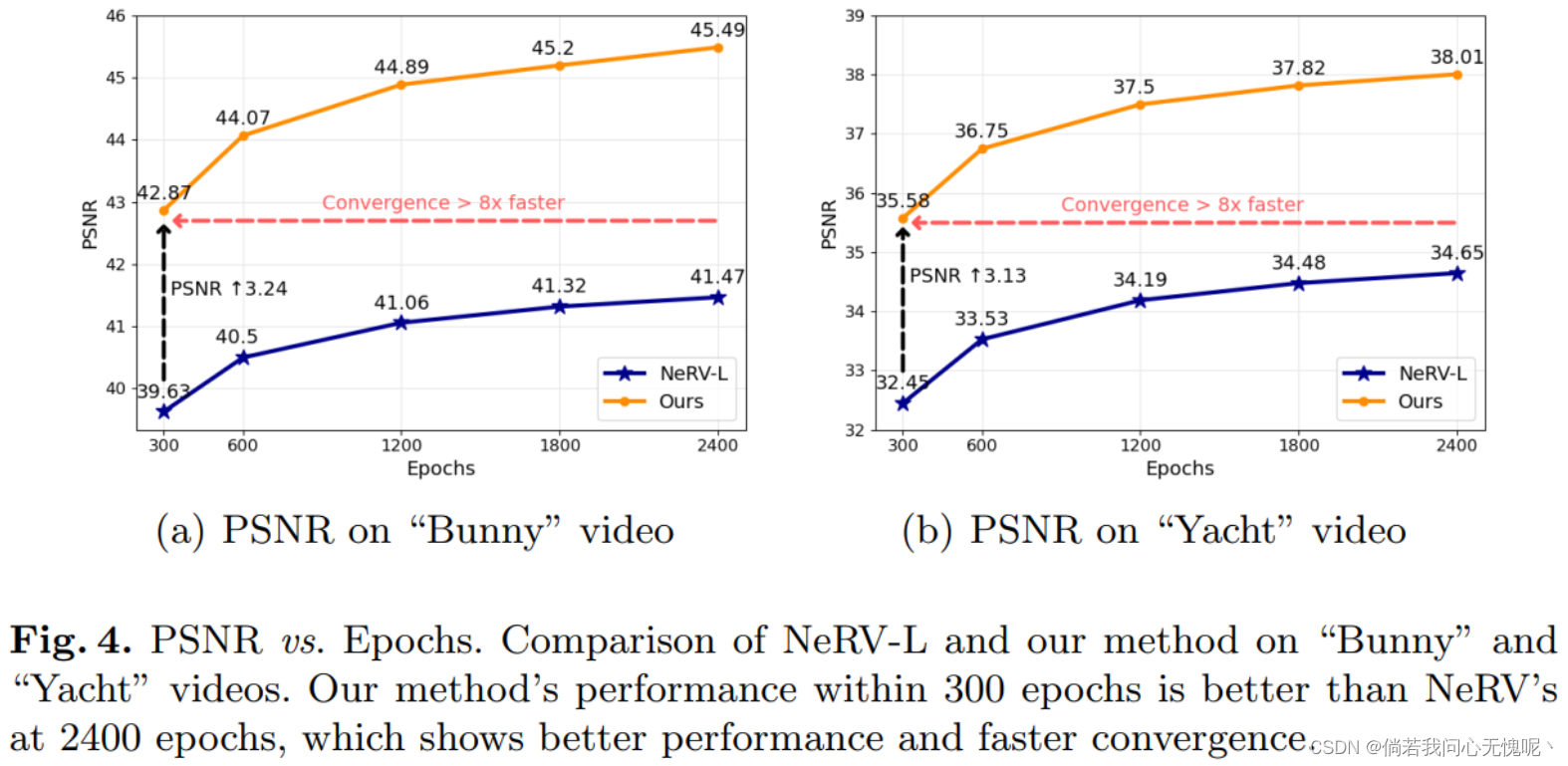
在这里插入图片描述
由于训练INR来拟合视频序列是一个过拟合的过程，较长的时间表自然会带来更好的性能。换句话说，如果提出的方法的性能超过另一种方法在相同的策略下，它保证了更好的性能和更快的收敛速度。在图4中，我们提供了我们的方法与NeRV在不同训练计划的“Bunny”和“Yacht”视频上的比较。我们的方法在300个时间点上的性能大大超过了基线。它也超过了基线在2400期的性能，收敛速度快了8倍。实际上，在所有不同的视频中，我们的方法在300 epoch时的性能优于基线在2400 epoch时的性能。我们在补充部分提供了详细的结果。
在这里插入图片描述

5.4 Comparison with Alternatives

我们将我们的方法与试图删除冗余参数或在Eq. 3中进行 $F_\theta$ 融合的四种替代方法进行比较:

NeRV- $C_s$ :由于输出大小为 $C \times h \times w$ 的MLP的最后一层参数过多，我们增加了一个低于 $C$ 的中间通道尺寸 $C_s$ 。MLP输出大小为 $C_s×h×w$ 的特征图，随着一个 $\times 1$ 的卷积将通道维度提升到 $C$ ，与NeRV块之前的原始设置相同。
NeRV-Split:受[20]中分裂结构的启发，我们重新设计了MLP结构，让它输出大小为 $C \times (h + w)$ 的张量，然后将其分成大小分别为 $C \times h$ 和 $C \times w$ 的两部分。通过张量积生成所需的 $C \times h \times w$ 特征图 $f_t$ 。
E-NeRV-MLP:由于 $F_θ$ 函数负责时空背景的特征融合，所以任何融合操作都可以。我们用连续两个空间通道为 $(h \times w)$ 和特征信道为 $(C)$ 的MLP替换了包含注意力模块的小型Transformer。
E-NeRV-Conv:我们使用 $\times 3$ 卷积块替换Tranformer块。卷积块融合窗口区域内的特征，并以滑动窗口的方式扫描整个特征映射。

结果如表2所示。为了公平比较如何降低参数的大小，我们建立了我们的方法的两个版本：我们删除了4.1中描述的在卷积块阶段引入时间上下文的部分结构，因为它可以进一步提高性能，并减小了卷积的信道维度，使得到的模型的参数大小与两个备选方案的大小相同。可以看出，在相似的参数设置下，我们的方法优于这些方法。

对于 $F_\theta$ 的特征融合方案，Transformer相比MLP或Conv能带来增量的性能增长，但三种模型都能以较大的优势击败NeRV-L。解纠缠的表示和结构本身可以显著降低尺寸，因此我们可以将保存的参数分配到卷积中以获得更好的性能。随着视觉变压器研究的快速发展，任何其他更复杂的结构，如变压器和卷积的结合，也受到欢迎，并可能进一步提高性能。我们说明，在一些内容几乎静止的视频中，如“美女”和“蜜蜂”，与动态视频相比，每种选择之间的差异很小。由于指标是在所有视频中平均的，所以备选方案之间的差异在表2中也可能是递增的，但在8个视频中部分排序关系是相同的。
在这里插入图片描述

5.5 Ablation Studies

在本节中，我们将研究我们提出的方法的三个新组成部分的影响:在网络的开始处引入空间融合函数 $Φ$ 、时空融合 $F_θ$ 和时间实例归一化方法，在每个卷积块中引入时间上下文。对所有的视频序列进行消融实验，并对得到的指标进行平均。如表3所示，E-NeRV的性能随着这些模块的逐渐增加而提高，并且这种递增的特性存在于所有实验视频序列中。值得注意的是，“Variant1”，在卷积阶段没有融合和时间上下文，在不同的视频序列中，仍然可以在两个指标上优于基线。更具体地说，简单地使用提出的解纠缠公式减少冗余参数并将其分布到下面的卷积块中，得到的具有相似参数的模型已经超过了NeRV-L。 我们认为这在一定程度上进一步证明了解纠缠动机的有效性。

5.6 Downstream application results

除了表示能力外，我们还比较了E-NeRV与NeRV在视频INR的不同下游任务上的性能，包括视频去噪和压缩。结果如表4所示。

两个实验都遵循NeRV的管道，我们进一步进行了不同修剪比的消融压缩。PSNR指标是所有视频序列的平均值。在去噪结果中，“噪声”指的是任何去噪之前的噪声帧。这里我们只与NeRV进行比较，因为他们在论文中击败了其他基于过滤和基于学习的方法。E-NeRV的去噪结果也证明了我们的解纠缠空间表示的优势，这是视频去噪的一个空间先验。

在压缩实验中，两种方法的性能都随着压缩比(图中Sparsity)的增加而下降，但E-NeRV在不同压缩比下的性能都较好。结果还表明，在E-NeRV中，基于帧的视频INR的压缩能力(即在压缩视频序列时修剪网络权值的管道)保持不变。详细的总体结果可以在附录中找到。
在这里插入图片描述

5.7 Temporal frequency analysis

傅里叶特征映射的频率对INR的表示能力[47]有很大影响。较小的频率可能导致输入之间的平滑，适合插值，但也会降低INR对训练点的拟合。在本节中，我们研究了不同频率对解纠缠表示的影响。我们以3:1的比例将视频分成可见帧和不可见帧两部分，调整频率，在我们的一般设置是1.25。结果如图5所示。
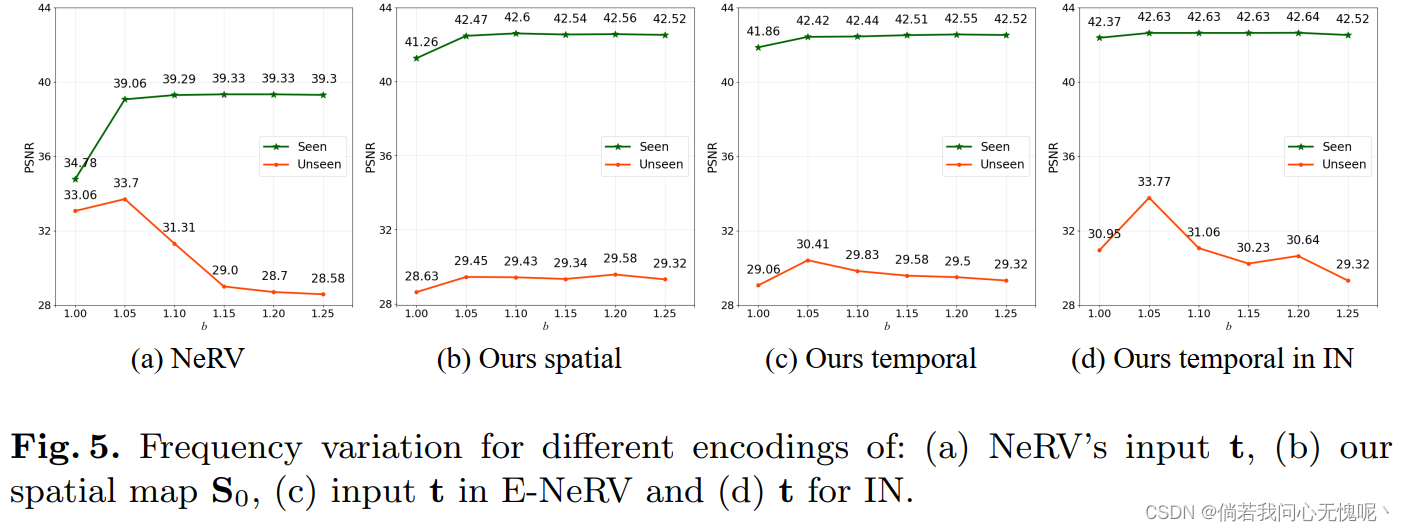
在这里插入图片描述
从NeRV在频率1.25处的插值(39.3/28.58)开始，我们可以看到，由于NeRV以耦合的方式考虑空间和时间，降低频率可以提高插值，但也会导致所见帧的性能下降(图5 (a))。相反，我们的解纠缠表示允许在三种编码中操纵频率:空间网格坐标、时间输入t和时间实例归一化中使用的t。具体来说，将In模块中的频率从1.25调整到1.05，可以在保持训练点性能的同时得到最优插值(图5 (d))，这可以被认为是我们的解纠缠结构的另一个优点。更多的数据集划分细节，插值结果和可视化可在补充。

6. Conclusion

在本文中，我们提出了一种图像级视频隐式表示，具能够将空间和时间上下文解纠缠。在之前基于图像的视频INR[2]的基础上，与基于像素的视频INR相比，我们的方法保留了其在训练和推理速度上的优势[47,43,27]，但在性能和收敛速度上有较大提升。我们定量地表明，我们提出的解纠缠结构和其他修改可以大大减少原有的不必要和冗余的参数。通过对保存的参数进行重新分配，我们的方法在参数更少的情况下性能更好，收敛速度快8倍。实验分析了该方法中各分量在不同视频序列上的作用。

最后，我们认为通过对我们的解纠缠表示应用更有效和更复杂的特征融合方法可以进一步改进我们的方法。在未来的工作中，我们计划将我们的图像视频INR应用于其他下游任务，如光流估计和视频超分辨率。