图的路径搜索

1. 深度优先遍历(Depth-First Traversal)

2.1 图的深度优先遍历的递归定义

　　假设给定图G的初态是所有顶点均未曾访问过。在G中任选一顶点v为初始出发点(源点)，则深度优先遍历可定义如下：首先访问出发点v，并将其标记为已访问过；然后依次从v出发搜索v的每个邻接点w。若w未曾访问过，则以w为新的出发点继续进行深度优先遍历，直至图中所有和源点v有路径相通的顶点(亦称为从源点可达的顶点)均已被访问为止。若此时图中仍有未访问的顶点，则另选一个尚未访问的顶点作为新的源点重复上述过程，直至图中所有顶点均已被访问为止。
　　图的深度优先遍历类似于树的前序遍历。采用的搜索方法的特点是尽可能先对纵深方向进行搜索。这种搜索方法称为深度优先搜索(Depth-First Search)。相应地，用此方法遍历图就很自然地称之为图的深度优先遍历。

1.2 深度优先搜索的过程

设x是当前被访问顶点，在对x做过访问标记后，选择一条从x出发的未检测过的边(x，y)。若发现顶点y已访问过，则重新选择另一条从x出发的未检测过的边，否则沿边(x，y)到达未曾访问过的y，对y访问并将其标记为已访问过；然后从y开始搜索，直到搜索完从y出发的所有路径，即访问完所有从y出发可达的顶点之后，才回溯到顶点x，并且再选择一条从x出发的未检测过的边。上述过程直至从x出发的所有边都已检测过为止。此时，若x不是源点，则回溯到在x之前被访问过的顶点；否则图中所有和源点有路径相通的顶点(即从源点可达的所有顶点)都已被访问过，若图G是连通图，则遍历过程结束，否则继续选择一个尚未被访问的顶点作为新源点，进行新的搜索过程。

2. 图路径搜索实际问题

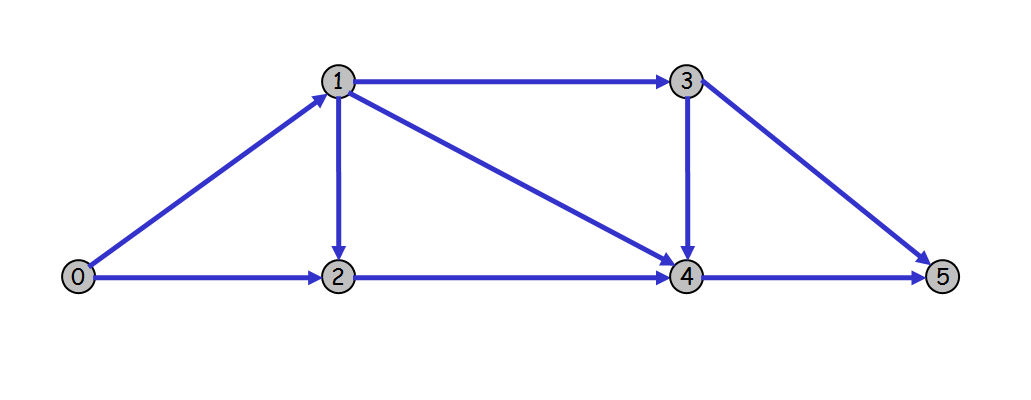
求下图中节点0到节点5的所有路径：

2.1 求解过程

第一步：建立相邻节点存储表，节点0与节点1和2；节点1与节点2、3和4；节点2与节点4；节点3与节点4和5；节点4与节点5；
第二步建立空栈，将其实节点0压人栈中；

1、 我们建立一个存储结点的栈结构，将起点0入栈，将结点0标记为入栈状态；
2、 从结点0出发，找到结点3的第一个非入栈状态的邻结点2，将结点2标记为入栈状态；
3、 从结点2出发，找到结点2的第一个非入栈状态的邻结点4，将结点4标记为入栈状态；
4、 从结点4出发，找到结点4的第一个非入栈状态的邻结点5，将结点5标记为入栈状态；
5、 栈顶结点5是终点，那么，我们就找到了一条起点到终点的路径，输出这条路径；
6、 从栈顶弹出结点5，将5标记为非入栈状态；
7、 现在栈顶结点为5，结点5没有除终点外的非入栈状态的结点，所以从栈顶将结点5弹出；
8、现在栈顶结点为4，结点4除了刚出栈的结点5之外，没有非入栈状态的相邻结点，那么我们将结点4出栈；
9、现在栈顶为结点2，结点2除了刚出栈的结点4之外，没有非入栈状态的相邻结点，那么我们将结点2出栈；
10、现在栈顶结点为0，从节点0出发，找到结点0的第一个非入栈状态的邻结点1，将结点1标记为入栈状态；一直查找到终点节点5。
11、重复步骤7-11，就可以找到从起点3到终点6的所有路径；
12、栈为空，算法结束。

求解详细代码如下：

#include <iostream>
#include <map>
using namespace std;
class node
{
public:
    int number;
    node *next;
    node(int a,node *b)
    {
       number=a;
       next=b;
    }
};

class stacks
{
    public:
    node * top;
    stacks(node * a=NULL)
    {
       top=NULL;
    }
    void push(int a)
    {
        if (top==NULL)
            top =new node(a,NULL);
        else top=new node(a,top);
    }
    void pop()
    {
       node *b=top;
       top=top->next;
       delete b;
    }
}; //保存已加入路径结点的栈
node* neighbour(int a);// ,int b
int cur_node;//当前结点，即为栈顶的结点
int next_node=8 ;//当前结点的下一个邻接点，即刚从栈顶弹出的结点，初始化为8
map<int,int> map_next;//每个结点的下一个邻接点，即刚从栈顶弹出的结点

int start=0;
int end=5;//起点为3，终点为6
stacks aray[6]={stacks(NULL),stacks(NULL),stacks(NULL),stacks(NULL),stacks(NULL),stacks(NULL)};
stacks stack(NULL);
int states[6];//保存结点状态的数组
int main()
{
    //初始化map_next
    for(int i=0;i<=5;i++)
    {
       map_next[i] = -1;
    }
    //初始化节点邻接表的信息  
    aray[0].push(1);aray[0].push(2);
    aray[1].push(2);aray[1].push(3);aray[1].push(4);
    aray[2].push(4);
    aray[3].push(4);    aray[3].push(5);
    aray[4].push(5);
    stack.push(start);//将起点入栈
    states[start]=1;//将起点标记为入栈状态
    node* tempnode=neighbour(3);
    cout<<"邻居节点："<<tempnode->number<<"下一个节点：" <<tempnode->next <<endl;
    int path[6];int len=0;
    while(NULL != stack.top) {//栈不为空
        if (stack.top->number==end){
            cout<<"end->start:   ";
            node* abc=stack.top;
            int i;
            i=0;
            while(abc->number != start){

                cout<<abc->number<<",";

                path[i++]=abc->number;
                abc=abc->next;
            }
            len=i+1;
            cout<<start <<" "<<"路径节点数="<<len<<endl;
            //cout << "start"<<endl;//输出已找到的路径
            stack.pop();//将栈顶结点弹出
            states[end]=0;//清除终点的状态
            map_next[end]=-1;
        }
        else{
            cur_node=stack.top->number;
            if(neighbour(cur_node) != NULL){//邻居不为空
                node *d =neighbour(cur_node);
                map_next[cur_node] = d->number;
                cur_node=d->number;
                stack.push(cur_node);
                states[cur_node]=1;
            }
            else{
                stack.pop();
                states[cur_node]=0;//删除的栈顶节点states置为0  通过该节点到不了目的地 
                map_next[cur_node] = -1;
            }
        }
    }
    return 0;
}

node* neighbour(int a){//,int b
    node *abc=aray[a].top;
    while ((NULL!=abc)){//结点abc不空
        if( states[abc->number]==1 )//邻居节点已经在栈stack里了
        {
            abc=abc->next;//所有的邻居节点初始化成一个栈了，继续找下一个邻居节点 
        }
        else//不在栈stack里
        {
            if(-1 == map_next[a])//就要abc作为返回值  如果a是最栈顶节点 
            {
                while(NULL!=abc && states[abc->number]==1)
                {
                    abc = abc->next;
                }
                return abc;
            }
            else if(abc->number == map_next[a])  //判断当前节点是否是a节点的邻居节点 
            {
                abc=abc->next;
                while(NULL!=abc && states[abc->number]==1)
                {
                    abc = abc->next;
                }
                return abc; //将abc的下一个结点返回
            }
            else
            {
                abc=abc->next;
            }
        }
    }
    return NULL;
}

程序运行结果如下；