Codeforces Round #396 (Div. 2) - Problem C - Mahmoud and a Message

题目链接：http://codeforces.com/contest/766/problem/C

开始的时候直接想到dfs，然后估摸着会超时，然后却选择性忽略了，因为写着写着就瞎掰出了一个故事：

n个年轻人在一片未开发的市场上创业的故事，故事最后的结局是超时。。

dfs实质还是遍历搜索，我没有剪枝（不知道咋剪），重复计算量太大，所以写完以后不仅是超时，而且是爆超。。test4就t了。。

无限制的情况下：                  铁定超啊。。

超时Dfs代码（纪念一下，哈哈）：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <string>
#include <cmath>
#include <vector>
#include <queue>
#include <stack>
#include <set>
#include <map>

using namespace std;

#define FOR(i,k,n) for(int i=k;i<n;i++)
#define FORR(i,k,n) for(int i=k;i<=n;i++)
#define scan(a) scanf("%d",&a)
#define scann(a,b) scanf("%d%d",&a,&b)
#define scannn(a,b,c) scanf("%d%d%d",&a,&b,&c)
#define mst(a,n)  memset(a,n,sizeof(a))
#define ll long long
#define N 1005
#define mod 1000000007
#define INF 0x3f3f3f3f

const double eps=1e-8;
const double pi=acos(-1.0);

int n;
char s[N];
int mLen[26];
ll tot;
int maxLen;
int minCnt;

void Dfs(int i,int cnt)//以i为首，i要创建公司
{
    //cout<<"test";
    if(i==n)
    {
        tot++;
        minCnt=min(minCnt,cnt);
        return ;
    }
    int j=i+1;
    int minLen=mLen[s[i]-'a'];//董事会的要求
    while(j<i+minLen&&j<n)//经董事会协商同意
    {
        if(j-i+1<=mLen[s[j]-'a'])
        {
            Dfs(j,cnt+1);//年轻人同意了，但为了自己当初的梦想仍要先出去闯荡一下，去创下业先
            //年轻人闯荡归来，进入董事会，成为董事会一员
            maxLen=max(maxLen,j-i+1);
            minLen=min(minLen,mLen[s[j]-'a']);
            j++;
        }
        else
        {
            //Dfs(j,cnt+1);//1.董事会同意但年轻人自己不同意，不愿为人臣，自己去开天辟地
            break;
        }
    }
    //if(j>=i+minLen)//2.董事会不同意，年轻人只能去自立门户
    //if(j<i+minLen&&j>=n)//3.董事会同意，但没人了，j==n要进入Dfs进行计数
    //if(j>=i+minLen&&j>=n)//4.董事会不同意，刚好也没人了，j==n要进入Dfs进行计数
    Dfs(j,cnt+1);//1234四种情况整合到一起
}

int main()
{
    //freopen("in.txt","r",stdin);
    //freopen("out.txt","w",stdout);

    cin>>n>>s;
    for(int i=0;i<26;i++)
        cin>>mLen[i];
    minCnt=INF;
    maxLen=1;
    Dfs(0,0);
    cout<<tot<<endl<<maxLen<<endl<<minCnt<<endl;
    return 0;
}

看到别人用dp，开始换思路，从数据规模上看也应该猜到大概是 的dp，两重循环，但是自己只能想到 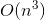的，还对着数据调了好久，可能数据不强，竟然让我擦着时限过了

dp思路：相邻项的数据关系

分成了两部分，第j项不和前面匹配 与 第j项和前面匹配

dp[i][j] = dp[i][j-1]（第j项不和前面匹配） +  { dp[i][k-1] | 从第k项到第j项可以匹配 }

dp[i][j]：从第i项到第j项分段方法总数，包括i,j

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <string>
#include <cmath>
#include <vector>
#include <queue>
#include <stack>
#include <set>
#include <map>

using namespace std;

#define FOR(i,k,n) for(int i=k;i<n;i++)
#define FORR(i,k,n) for(int i=k;i<=n;i++)
#define scan(a) scanf("%d",&a)
#define scann(a,b) scanf("%d%d",&a,&b)
#define scannn(a,b,c) scanf("%d%d%d",&a,&b,&c)
#define mst(a,n)  memset(a,n,sizeof(a))
#define ll long long
#define N 1005
#define mod 1000000007
#define INF 0x3f3f3f3f

const double eps=1e-8;
const double pi=acos(-1.0);

int n;
char s[N];
int mLen[26];
ll tot[N][N];
int maxLen;
int minCnt[N][N];

int main()
{
    //freopen("in.txt","r",stdin);
    //freopen("out.txt","w",stdout);

    cin>>n>>s;
    for(int i=0;i<26;i++)
        cin>>mLen[i];
    maxLen=1;
    for(int i=0;i<n;i++)
        for(int j=0;j<n;j++)
            minCnt[i][j]=N;
    mst(tot,0);
    for(int i=n-1;i>=0;i--)
    {
        for(int j=i;j<=n-1;j++)
        {
            //printf("*********[%d,%d]********\n",i,j);
            if(i<j)
            {
                tot[i][j]=tot[i][j-1];
                int k=j-1,tmp_max_len=mLen[s[j]-'a'];
                while(j-k+1<=tmp_max_len&&j-k+1<=mLen[s[k]-'a']&&i<=k-1)
                {
                    tot[i][j]=(tot[i][j]+tot[i][k-1])%mod;
                    tmp_max_len=min(tmp_max_len,mLen[s[k]-'a']);
                    maxLen=max(maxLen,j-k+1);
                    minCnt[i][j]=min(minCnt[i][j],minCnt[i][k-1]+1);
                    //printf("并入k=%d后，minCnt=%d\n",k,minCnt[i][j]);
                    k--;

                }
                if(i>k-1&&j-k+1<=tmp_max_len&&j-k+1<=mLen[s[k]-'a'])//k==i
                {
                    tot[i][j]=(tot[i][j]+1)%mod;
                    maxLen=max(maxLen,j-k+1);
                    minCnt[i][j]=1;
                    //printf("并掉i，minCnt=%d\n",minCnt[i][j]);
                }
                if(minCnt[i][j]==N) minCnt[i][j]=minCnt[i][j-1]+1;//printf("不能吞并任何，minCnt=%d\n",minCnt[i][j]);


            }

            else //i==j
                tot[i][j]=minCnt[i][j]=1;

        }
    }
    cout<<tot[0][n-1]<<endl<<maxLen<<endl<<minCnt[0][n-1]<<endl;
    return 0;
}

大神的 做法，发现我的想法饶了弯路，我的是"Z"型扫描线，大神的是"<"型扫描线，匹配的时候可以直接从前往后匹配啊！

cnt[i]：从i到末尾分段方法总数

#include <bits/stdc++.h>
using namespace std;

const int maxn = 1005, mod = 1e9+7;

int cnt[maxn], mn[maxn];

int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);

	int n;
	string s;
	cin >> n >> s;

	int a[26];
	for(int i = 0; i < 26; i++)
		cin >> a[i];

	int maxlen = 1;
	cnt[n] = 1;//配合递推式赋初值
	mn[n] = 0;//配合递推式赋初值
	for(int i = n-1; i >= 0; i--){
		int mx = maxn;
		mn[i] = maxn;
		for(int j = i; j < n; j++){
			mx = min(mx, a[s[j]-'a']);
			//cerr << i << " " << j << " " << mx << endl;
			if(mx < j-i+1) break;
			cnt[i] = (cnt[i] + cnt[j+1]) % mod;
			mn[i] = min(mn[i], 1 + mn[j+1]);
			maxlen = max(maxlen, j-i+1);
		}
	}

	cout << cnt[0] << "\n" << maxlen << "\n" << mn[0];

	return 0;
}