全错位排列有三种解法,嘿嘿,那我就要一探究竟!
一、递推
假设排列是1,2,3,4···n个数,Dn表示n个数的全错位排列的方法数。D1 = 0、D2 = 1
那么对于第1个位置,假设由k去占。现在就有两种情况:
1)、1和k互换了位置,k占1的位置,1占k的位置:那么此时相当于1和k位置确定,只需要讨论Dn-2的排列数。
2)、1没有占k的位置,而是占了其它的位置:那么此时相当于只确定了k的位置,需要讨论Dn-1的排列数。
但是有(n-1)个数需要讨论,所以可以得到下面的递推式:
然后等价变形为(两边同时处以n!,然后再移项整理):
然后展开递推式就可以得到错位排序的通项公式了。
二、容斥原理
记N(a1,a2,···,an)为n个数都没排错的方法数,那么对于以下情况,可以得到一些结论:
a1排对,记N(a1)=(n-1)!。因为a1已经排对了,那








 本文介绍了全错位排列的三种解法:递推法、容斥原理和母函数。通过详细阐述每种方法的思路,结合实例和公式推导,深入理解错位排列问题。并提供了相关练习题和参考资料。
本文介绍了全错位排列的三种解法:递推法、容斥原理和母函数。通过详细阐述每种方法的思路,结合实例和公式推导,深入理解错位排列问题。并提供了相关练习题和参考资料。
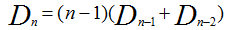
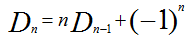
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 85
85

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








