为什么所有的世界地图都是“错”的？

当我们凝视世界地图时，是否曾怀疑过它的准确性？俄罗斯的国土面积仅为中国的1.8倍，但在传统地图上却显得庞大如三倍之巨；美国明明位于中国的西侧，却被标注为“东方”。

这些矛盾并非偶然，而是地图投影技术不可避免的产物。

本文将揭秘地图从球面到平面的转化过程，以及不同投影方法如何塑造了我们对世界的认知。

球面到平面无法避免的变形

地球是近似球体，而地图是二维平面。

将球面信息压缩到平面上，必然导致长度、面积、形状或方向的失真。

正如尝试将橘子皮平整展开时，边缘必然撕裂变形，地图投影的本质就是对这种“撕裂”的妥协。

将橘子皮平整展开

1829年，数学家高斯提出“橘皮定理”，橘子皮无法完美展开为平面，从数学层面证明了球面到平面的转化必然伴随变形。

将地球表面拉平

因此，地图投影的核心问题不是“是否失真”，而是“如何选择性失真”。

19世纪，德国数学家卡尔·弗里德里希·高斯通过数学严密证明了一个令人沮丧的结论，不存在一种既能保形又能保面积的完美投影。

卡尔·弗里德里希·高斯

这一论断如同达摩克利斯之剑，悬挂在所有地图制作者的头顶。

无论是追求方向精准的墨卡托投影，被广泛用于航海图，还是强调面积等比的高尔彼得斯投影，亦或是其他圆锥投影、方位投影方案，本质上都是在不同维度间的权衡取舍。

通用的世界地图版本“墨卡托投影” 

如何解决这个问题？

1500多年前，前辈们试图用各种方法把地球变成一个平面。

比利时地理学家格哈德斯墨卡托（Gerhardus Mercator）提出了地球被空心圆柱包围的假设基准面（赤道）与圆柱相切。    

基准纬线（赤道）与圆柱相切

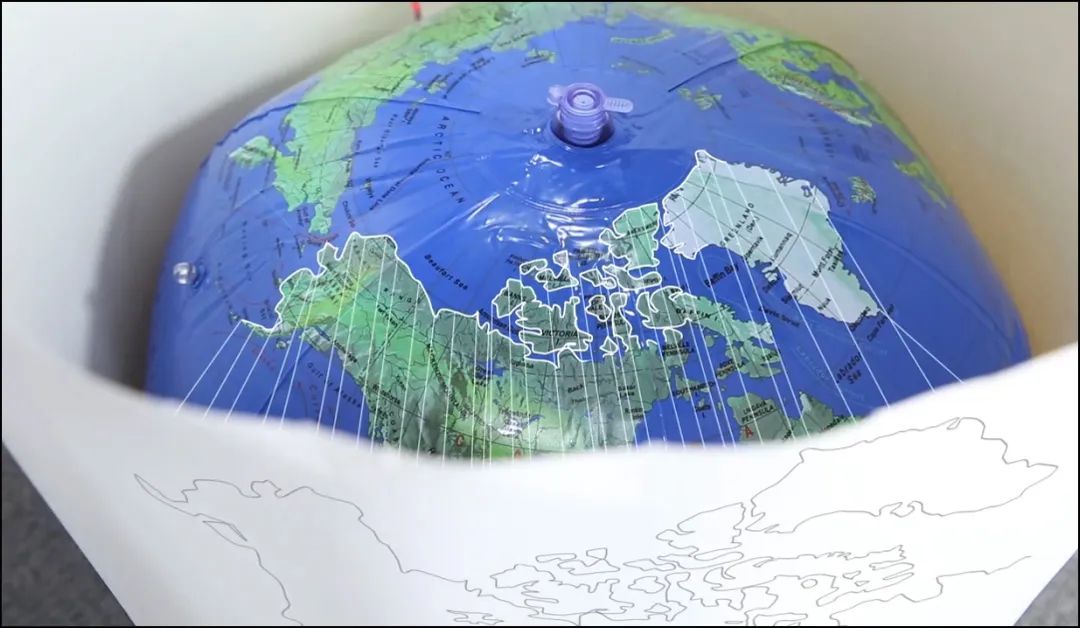
球面上的图形投影到圆柱体上

最后把圆柱体展开这就是一幅选定基准纬线的“墨卡托投影（Mercator）”绘制出的地图。

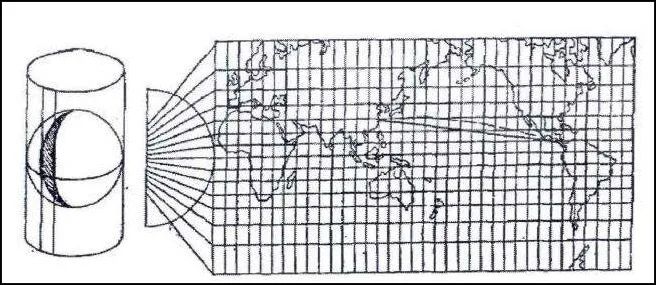
墨卡托投影

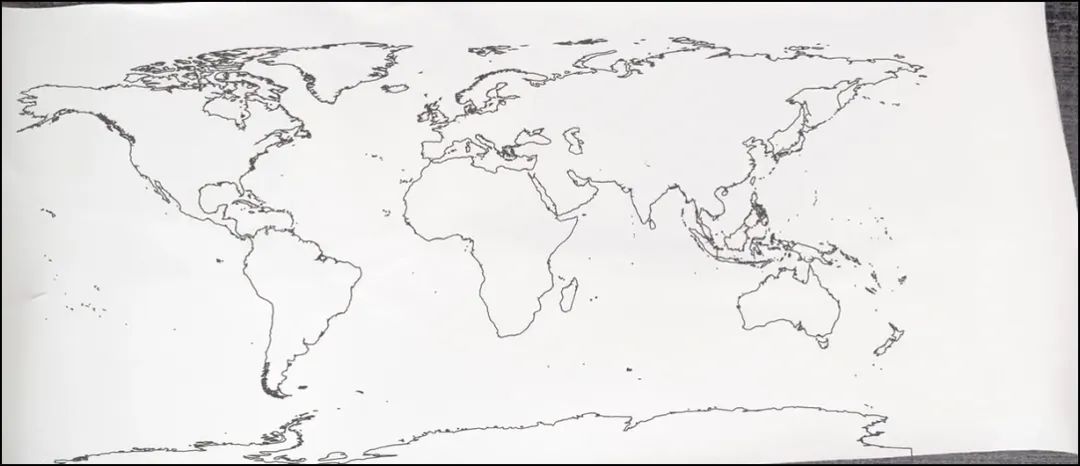
墨卡托投影

墨卡托投影将经纬网按等角条件投影到柱面上，然后将柱面展开成一个平面，得到一个平面经纬线网。    

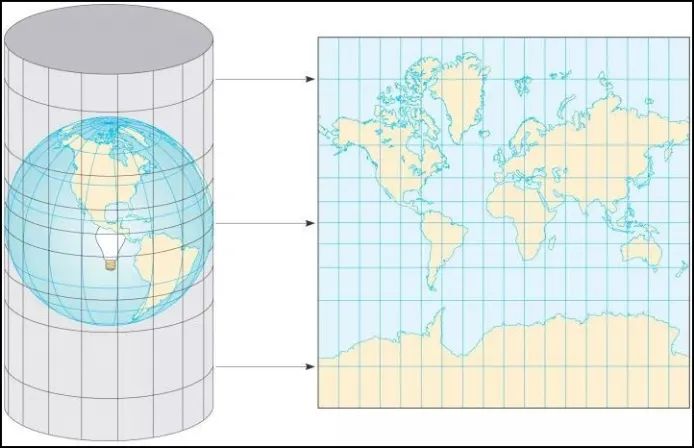
墨卡托投影

经投影后，子午线是一组垂直等距平行直线,纬度是一组垂直于经度的平行直线。

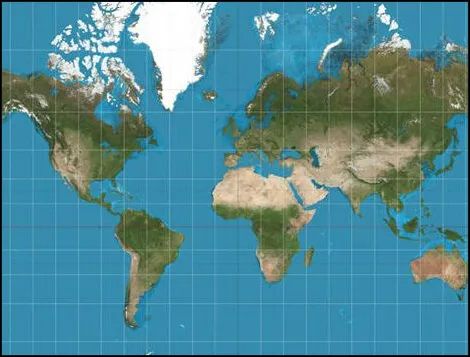
墨卡托投影

墨卡托投影上的任一点的任何方向的长度比均相等，即没有角度变形这也就意味着使用这种地图进行导航时能为地图上的两个点之间提供准确的角度。    

等距线以直线表示的特点，使其广泛应用于海图、航图的编制中。

这就是谷歌地图使用这种投影方法的原因,使用城市导航时。

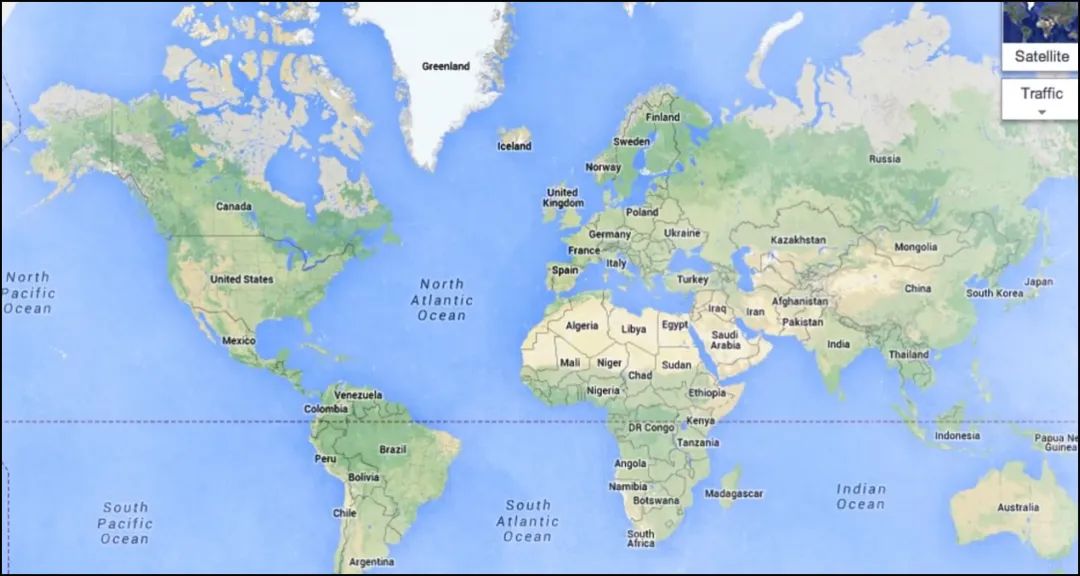
墨卡托投影可以确保转角不变形

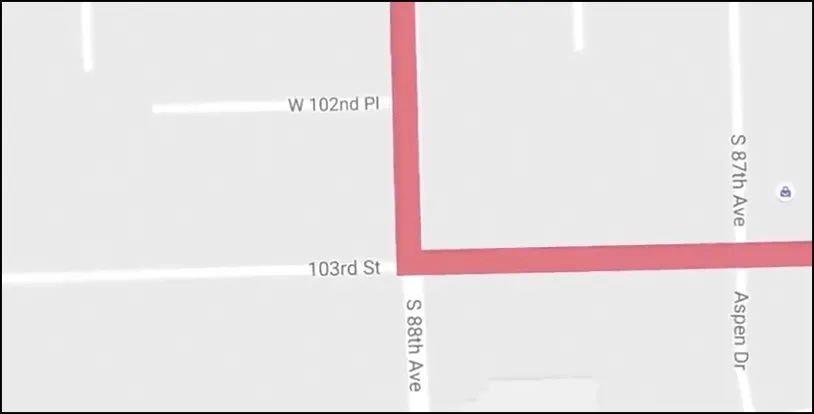
墨卡托投影可以确保转角不变形

墨卡托投影图首先确保每个国家的形状保持不变，但该地区的变形非常显著，并随着距离标准纬度的距离而增加。    

如果我们在地球上均匀分布同一区域的圆。

在墨卡托投影图上这些圆的面积会改变

圆圈的形状没有改变，但越靠近两极，面积就越大。

墨卡托投影地球面积面积变化

一个例子可以反映这种现象。

事实上，格陵兰岛的面积比非洲小得多。

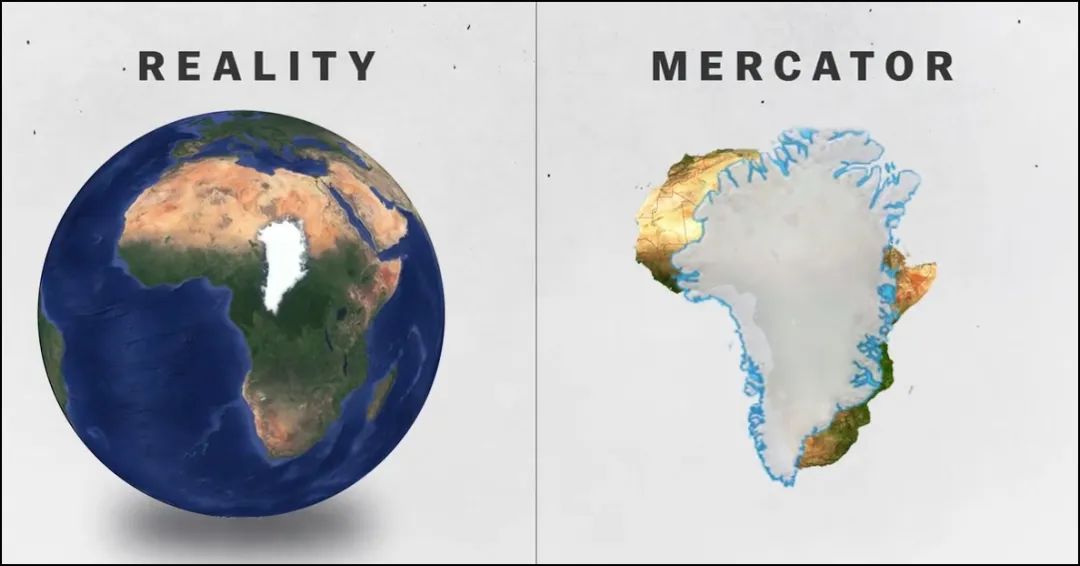
真实情况与墨卡托投影对比

但墨卡托投影图上的格陵兰岛面积几乎和非洲一样大。

高尔·皮德斯投影面积准确形状失真

如果我们想获得面积表示准确的地图可以使用等面积地图--高尔·彼得斯（Gall- Peters）投影世界地图。    

高尔彼得斯投影

高尔彼得斯投影世界地图是面积相等的地图投影。

它假设圆柱投影面和地球在南北纬30°（或50°）处切割。

根据球面透视法，将经纬度网络投影到等距圆柱体上。再沿一母线展成平面。

 高尔彼得斯投影

这种投影地图中各大陆比例基本正确，面积不发生变化但是扭曲了形状在水平面上，两极扭曲在垂直面上，赤道附近产生了扭曲比如非洲的面积是正确的但变得特别狭长我们可以再来对比一下格陵兰岛和非洲。

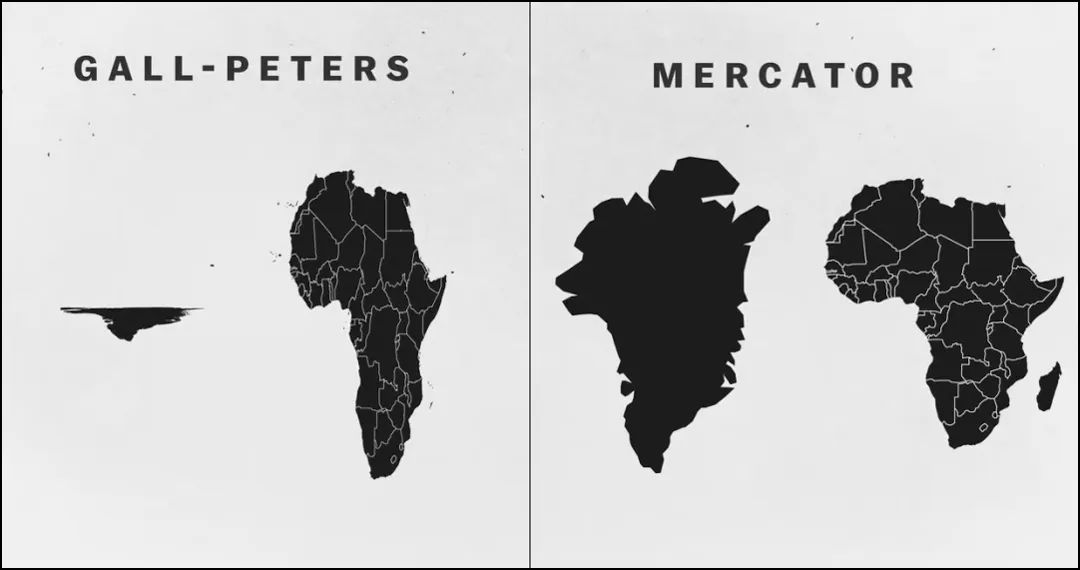
高尔彼得斯投影与墨卡托投影对比

面积比较看起来正常，但形状太“奇怪”。我们仍然使用等面积圆形进行演示。

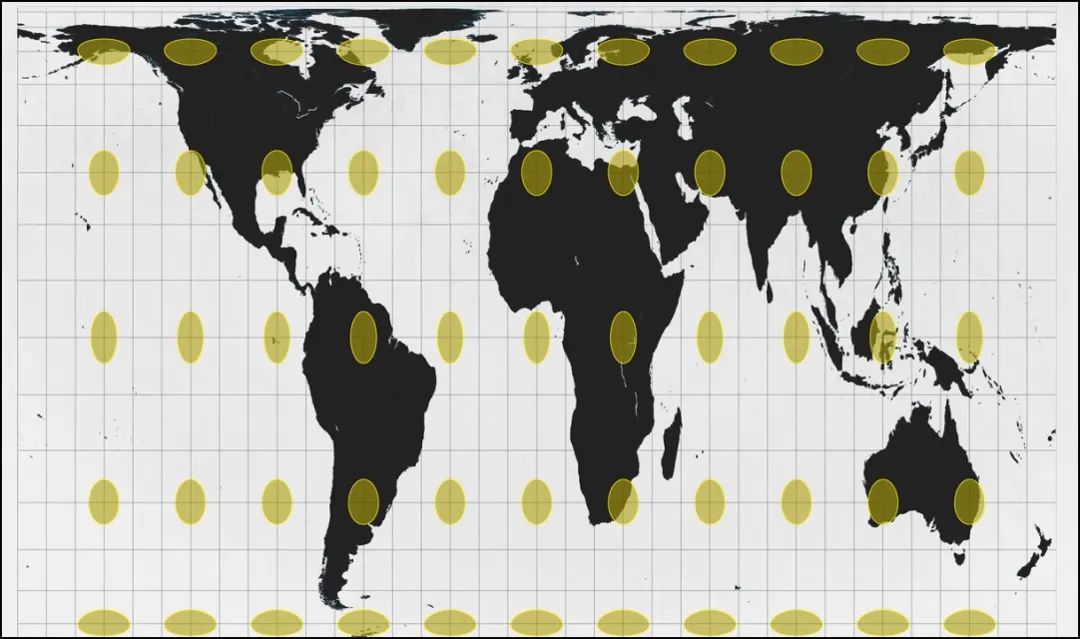
等面积圆形变化

可以看到高尔彼得斯投影世界地图中的圆形面积没有发生变化。

但几乎所有的形状都被拉成椭圆，两极被水平拉，赤道被纵向拉。

1998年美国国家地理学会使用了温克尔投影（Winkel Tripel）。

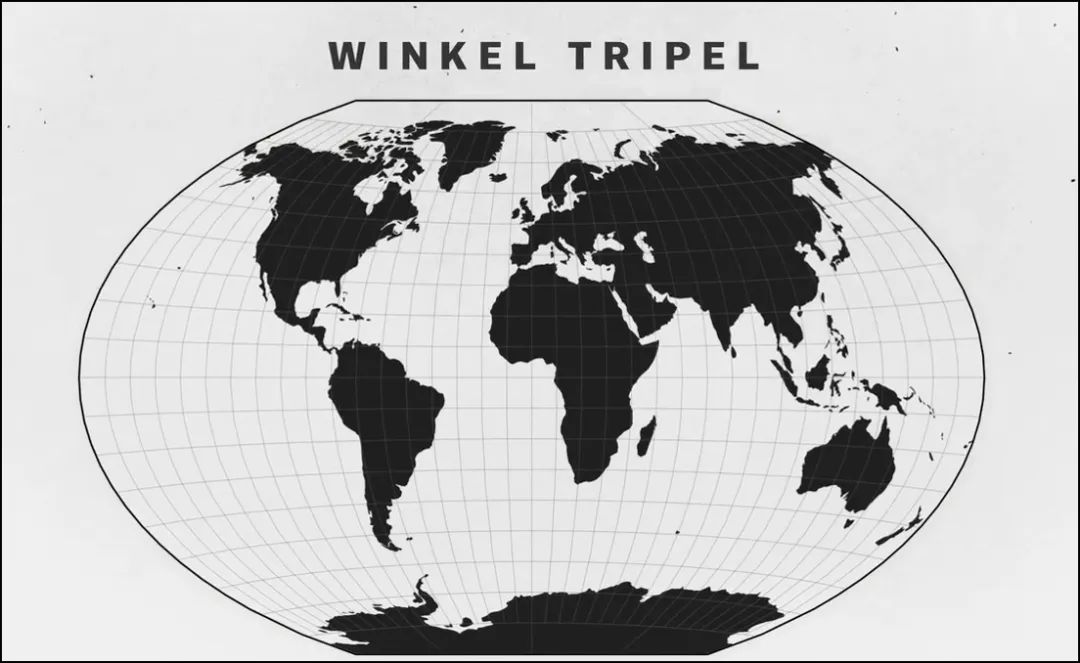
温克尔投影

因为这种投影方法可以在大小（面积）和形状之间达到最佳平衡性。

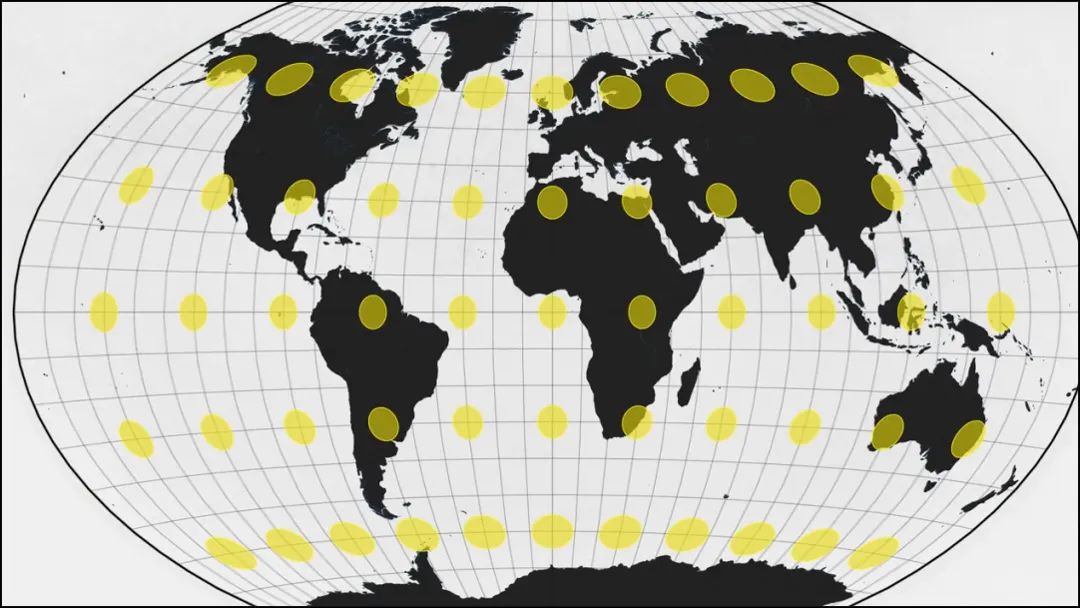
面积和形状之间达到最佳平衡

墨卡托投影和高尔·彼得斯投影只是圆柱投影中的投影方法之一。

根据轴的类型大致可分为正轴、水平轴和斜轴。

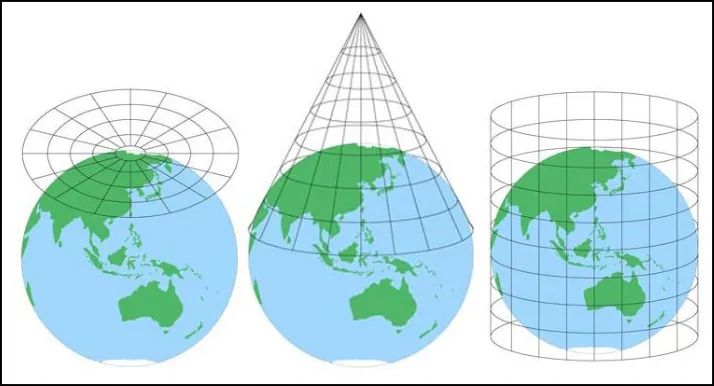
正轴、水平轴和斜轴

所以它至少可以分为九种不同的投影方法。    

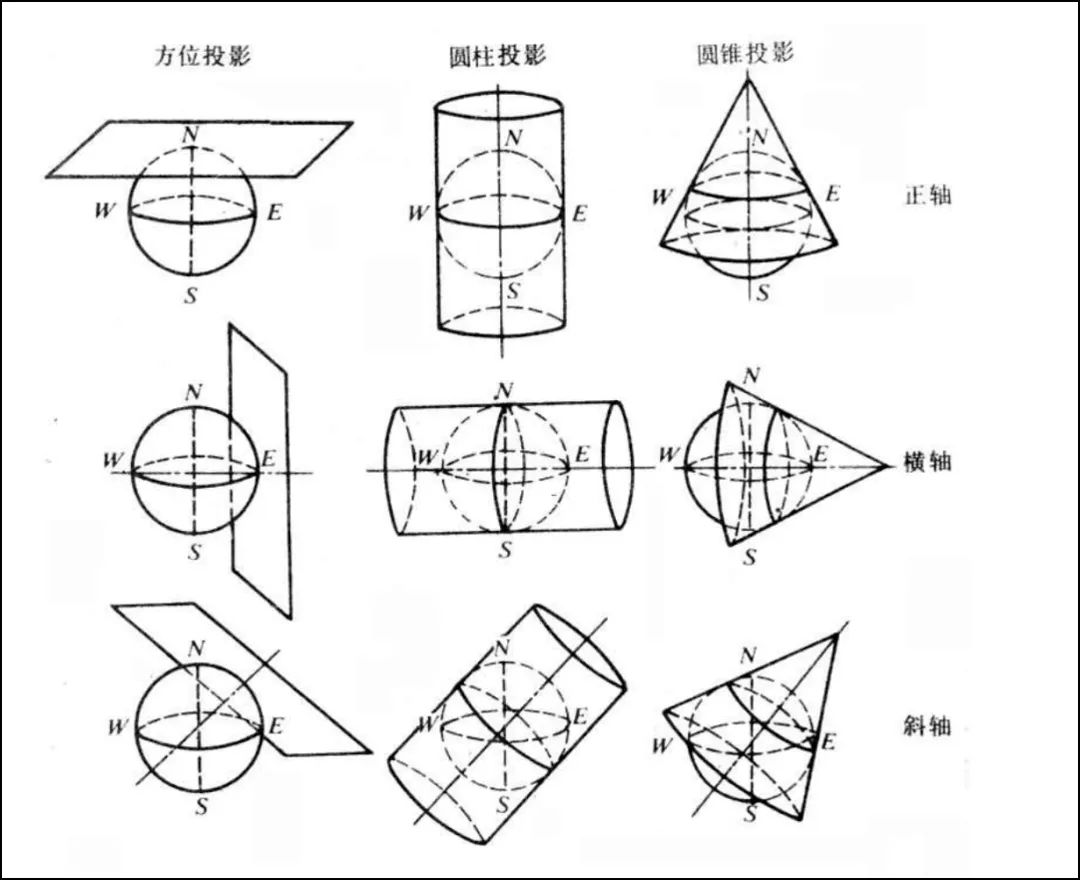
九种不同的投影方法

墨卡托投影和高尔·彼得斯投影就属于正轴圆柱投影一些常见的圆锥投影有等角正割圆锥投影、等距正割圆锥投影和等积正割圆锥投影。    

等角正割圆锥投影

等积正割圆锥投影

一些常见的方位投影有等积斜切方位投影和等角正切方位投影。    

等距正割圆锥投影

等积斜切方位投影

等角正切方位投影

古蒂等面积投影

此外，还有一些特殊的投影方法，如古德投影（Goodes-Homolosine），以保持大陆或海洋的完全分割。

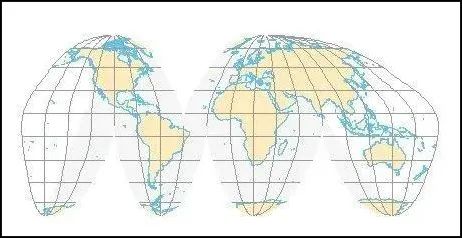
古德投影大陆

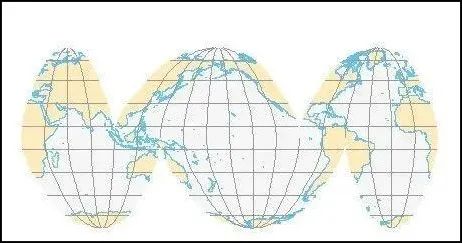
古德投影海洋

彭纳投影也叫心形投影是一种等面积伪圆锥投影。

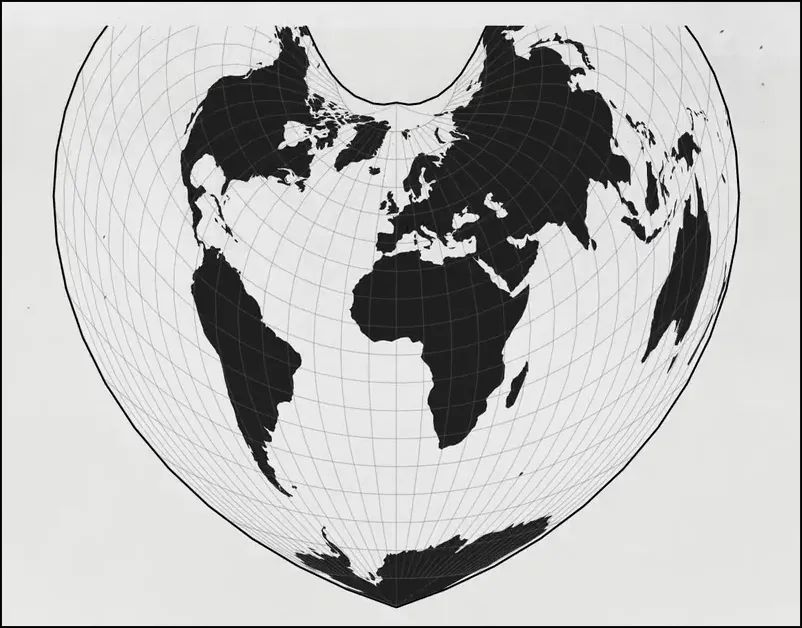
等面积伪圆锥投影

柏格斯星状投影（Berghaus Star）也被称为恒星投影，是美国地理学家协会（AAG）的标志。    

美国地理学家协会标注

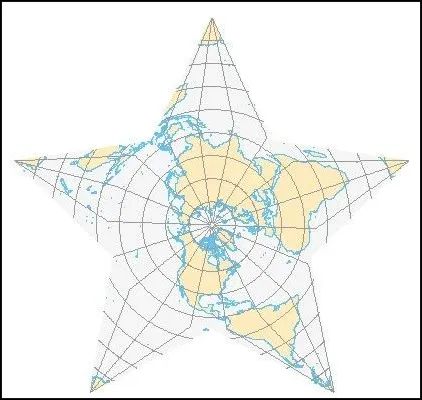
恒星投影

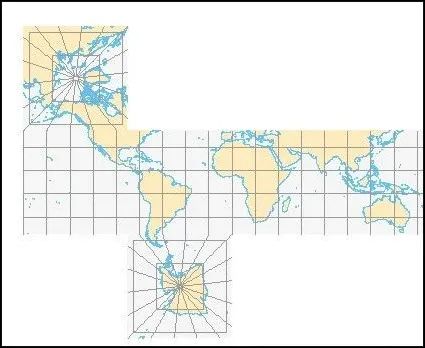
富勒投影

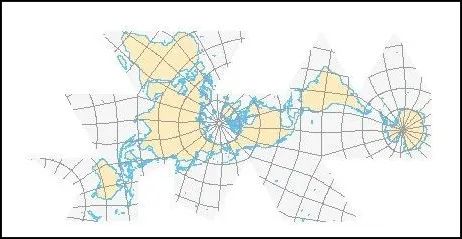
多圆锥投影

值得一提的是，联合国的标志使用的是以北极为中心的等距方位投影（Azimuthal Equidistant）。    

联合国的标志

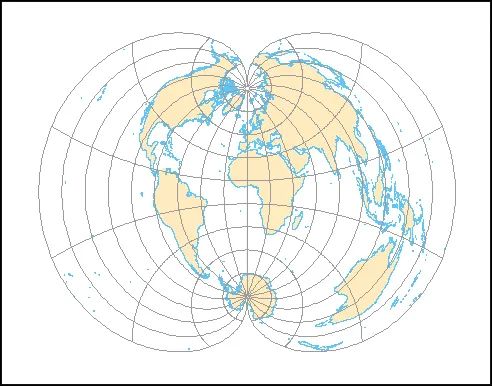
等距方位投影

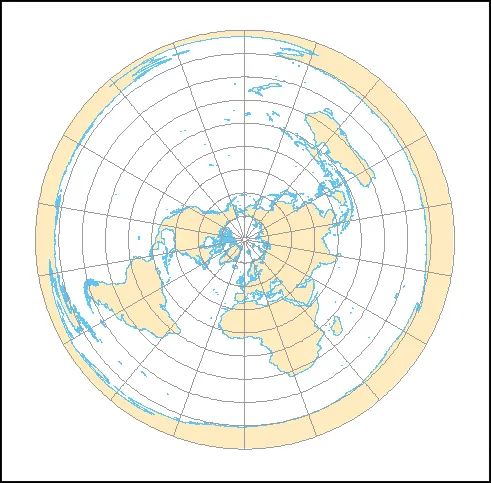
等距方位投影

为了满足航海、定位和航空航天的需要，地图学家和数学家已经产生了大量的地图库。

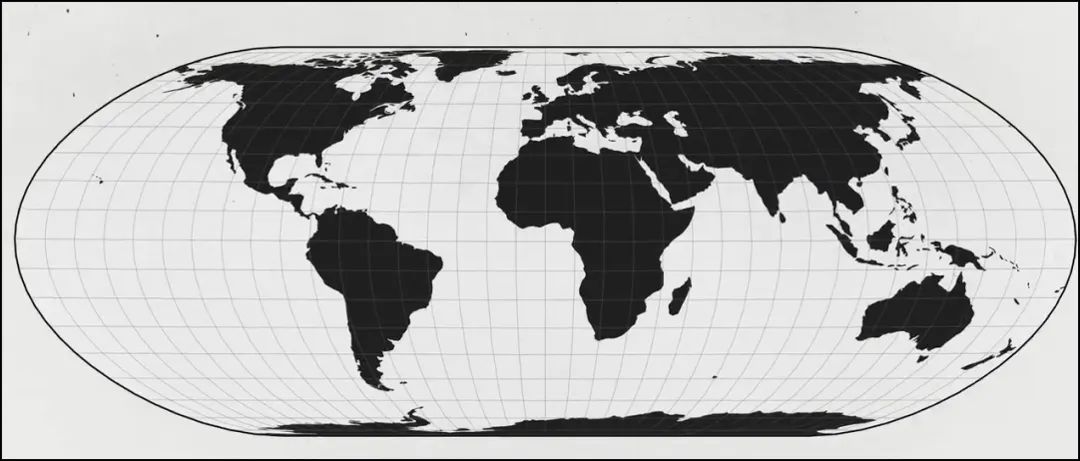
地图投影库

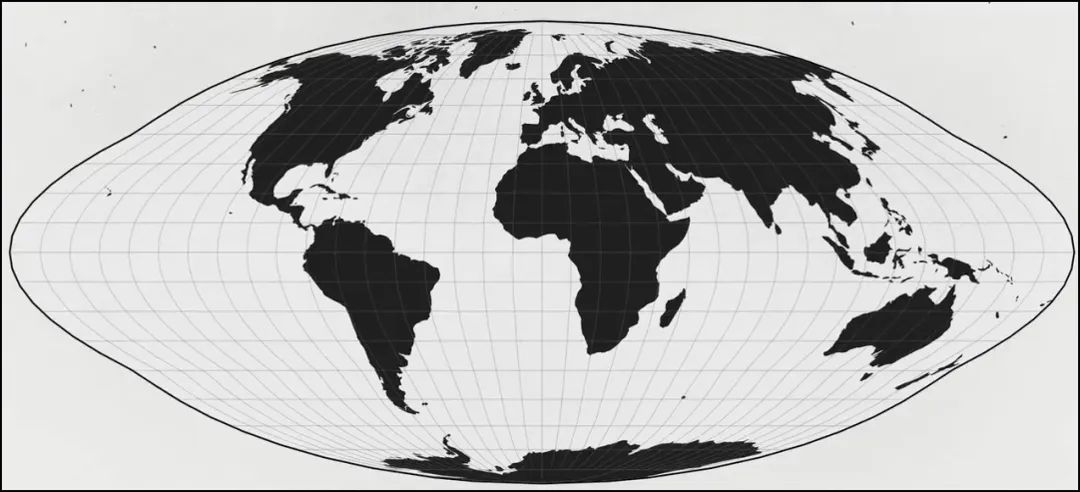
地图投影库

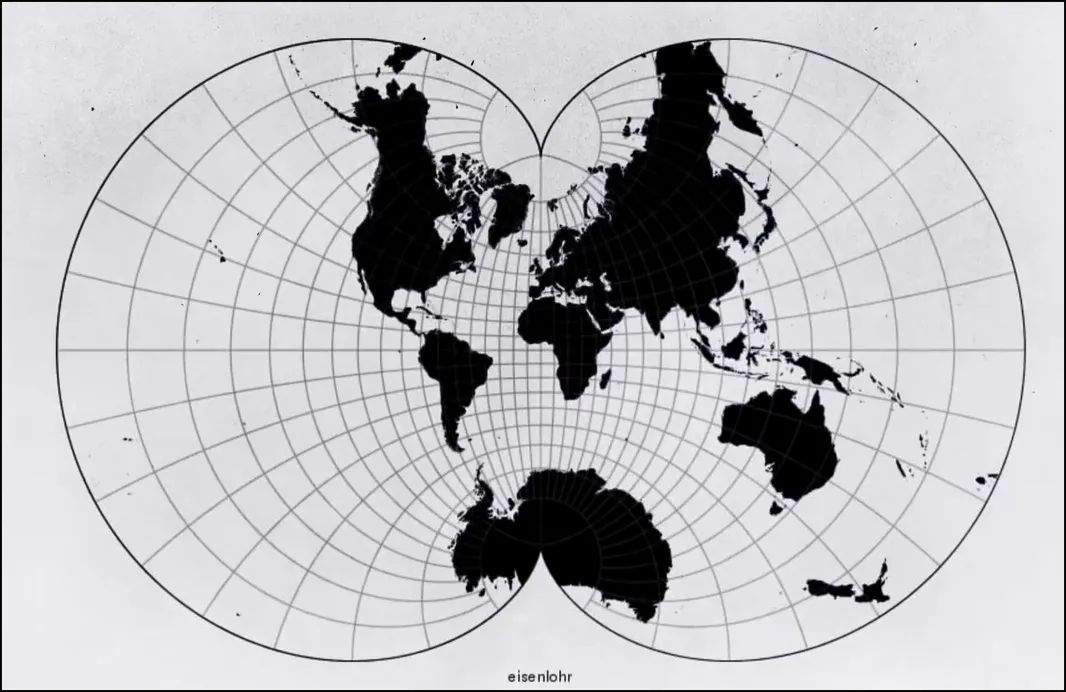
地图投影库

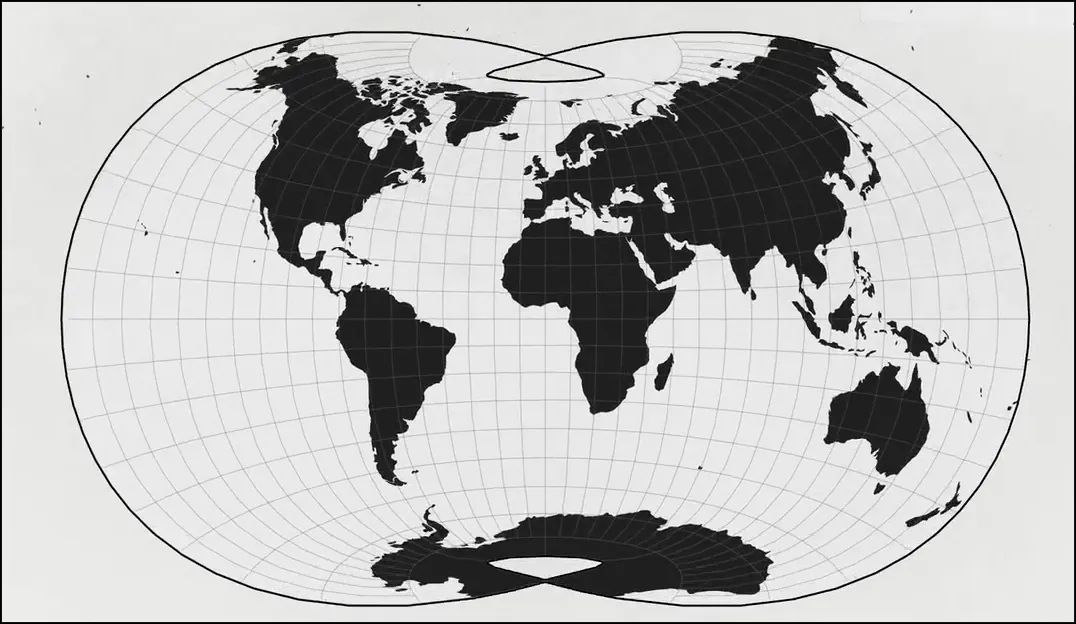
地图投影库

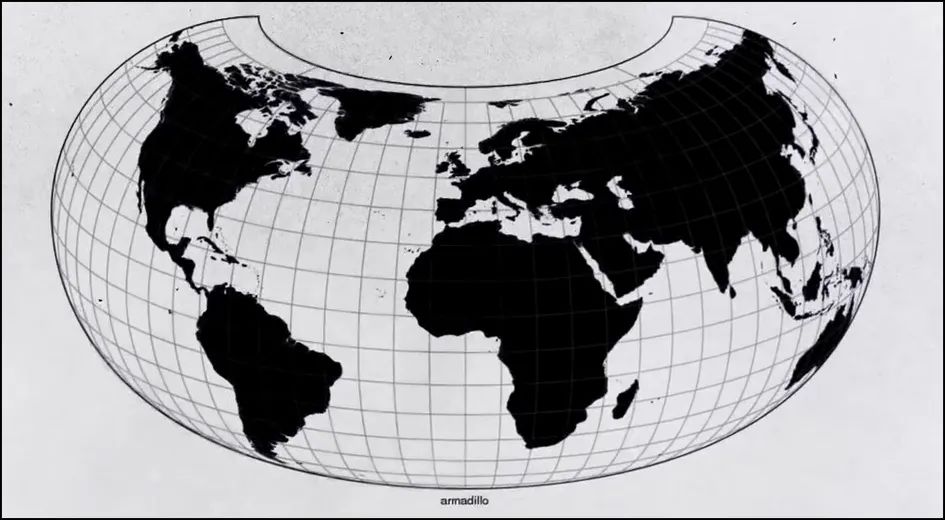
地图投影库

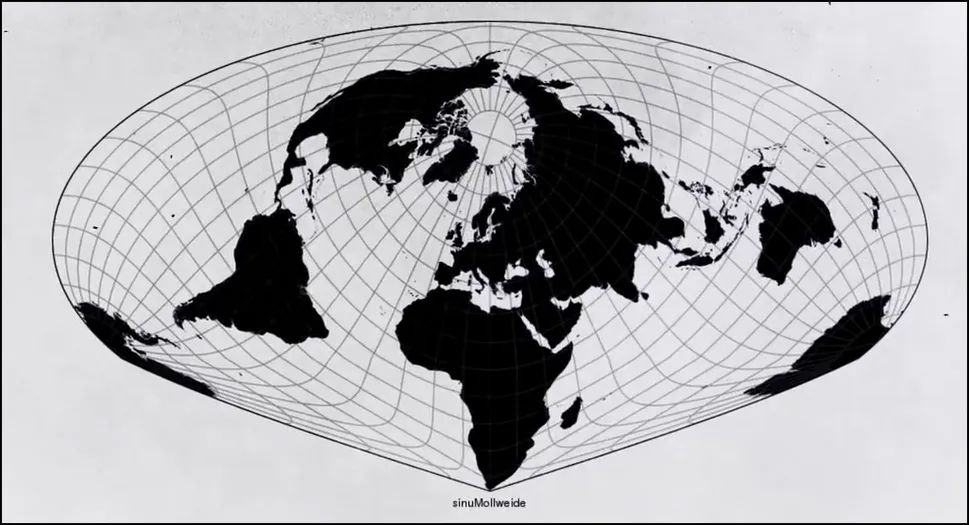
地图投影库

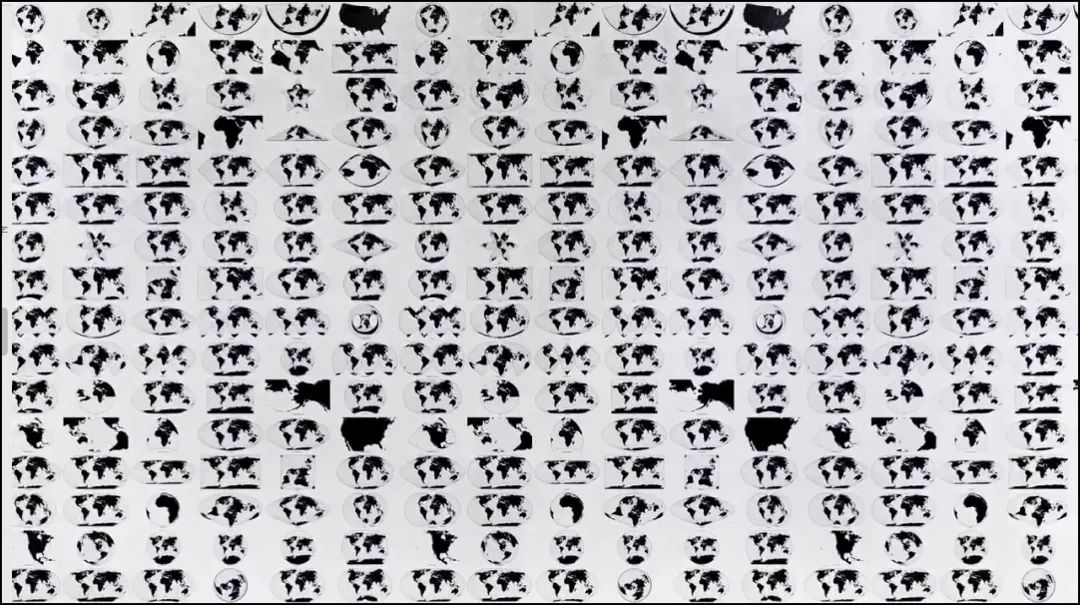
地图投影库

所有投影方法都如同“带缺陷的透镜”，透过它们看到的既是世界的片段，也是人类认知的镜像。

联合国徽章采用的等距方位投影，虽使极地国家严重变形，却巧妙地将北半球发达国家置于视觉中心，这种“无意识的选择”本身便值得深思。    

当我们使用地图时，重要的不是苛求“绝对正确”，而是清醒认知其构建逻辑：每张地图都是特定目的下的主观建构。

航海图需要方向精准，政治地图强调领土完整，气候研究侧重空间分布，理解这些隐性编码，我们才能真正读懂地图背后的权力叙事与认知博弈。

写在最后

当我们凝视地图时，不妨意识到：那些线条、色块和比例，是人类文明与自然规律博弈的产物。

下一次讨论“国家大小”时，或许应先问一句“你使用的是哪种投影？” 

在涉及国家主权的场合，请务必使用符合国家测绘标准的地图，以维护领土完整。

你可以立即点击“分享”按钮，将本文分享给你的朋友！