字符串处理之KMP算法

从暴力匹配到KMP

字符串匹配问题是程序设计竞赛中最常见的问题之一，如何用最优的时间复杂度的算法去解决这么一个问题是具有极大现实意义的。

我们先从最朴素的暴力匹配去开始这个问题。

现在给你两个字符串

我们暴力的从0位置去匹配，一直到$len1-len2$处为止，由此可见在最坏情况下，该思想的匹配算法的时间复杂度为$O(N^2)$，这样的时间复杂的适用范围肯定是很小的，那么如何提高匹配的时间效率呢?

在暴力匹配的过程中，我们每次成功匹配或者是失败匹配之后，都会将串的位置向后移1位，但是，通过观察字符串的特性，我们发现在移动之后前面某些位置的字符已经匹配过了，可是在暴力匹配中，我们再次匹配了一边，这就造成了时间复杂度的急剧增长。

下面我们来介绍KMP算法

KMP算法利用了字符串自身的性质，在每次失配之后使得字符串移动的距离最大。

同样的，我们先给出两个串

我们匹配到位置1，发现失配

此时我们移动的长度为1，有同学可能会问，这不是和我暴力一样吗！这个嘛，接着看接着看

这样一位一位移动，一直到了这里

好不容易匹配到最后一位了，然而发生了失配现象，那么这次我们要移动1位吗？
当然不！
我们官场前面已经匹配成功的前6位，他们的前缀和后缀的最大匹配长度为2，设其为$common$那么我们要向右移动$len（已匹配长度）-common$.

KMP的核心就是这么一点东西，是不是很简单很简单很简单！！！

我们来看看这次移动后它到了哪里

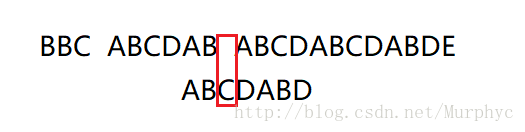
我们可以惊奇的发现移动后有2位已经是匹配完毕了的，这个匹配完毕的长度即为之前说的$common$，是不是很神奇！

我们先不考虑为什么他有这种性质，如果我们想直接去用这个性质，我们直接预处理出匹配串的每一个前缀的最大前缀后缀的匹配长度不就在$O（N）$的时间里解决了匹配问题了吗！

现在我们来讲讲为什么会有这种性质以及如何在$O(M)$的时间内求出失配指针，我们也可以叫他$Next[]$数组.

如果已有$p[0] ,p[1], ..., p[k-1] = p[j]-k, p[j]-k+1, ..., p[j]-1$，

此时$Next[j] = k$

这种情况实际上就是字符串开始的$k-1$个和当前位置$j$之前的$k-1$个对应相等

接着我们还可以发现

若$p[k]==p[j]$，则$Next[j+1]=Next[j]+1=k+1$

若$p[k]!=p[j]$，$k$索引$Next[k]$直到与$p[j]$相等，此时可用公式$Next[j+1]=k+1$

具体是为什么鉴于个人画图能力有限（lazy），我就不画了，给大家一个画的比较好的blog的链接。

画的是真的好

那么KMP就到此为止啦，最后贴个$Next$数组的模板。

char s[100005];

int Next[100005];

void getnext()
{
    int len=strlen(s);
    int j=-1;
    Next[0]=-1;
    int i=0;
    while(i<len)
    {
        if(j==-1||s[j]==s[i])
        {
            i++;
            j++;
            Next[i]=j;
        }
        else
            j=Next[j];
    }
}