LeetCode C++ 909. Snakes and Ladders【BFS/Graph】中等

On an N x N board, the numbers from 1 to N*N are written boustrophedonically starting from the bottom left of the board, and alternating direction each row.  For example, for a 6 x 6 board, the numbers are written as follows:

You start on square 1 of the board (which is always in the last row and first column).  Each move, starting from square x, consists of the following:

• You choose a destination square S with number x+1, x+2, x+3, x+4, x+5, or x+6, provided this number is <= N*N.
• (This choice simulates the result of a standard 6-sided die roll: ie., there are always at most 6 destinations, regardless of the size of the board.)
• If S has a snake or ladder, you move to the destination of that snake or ladder.  Otherwise, you move to S.

A board square on row r and column c has a "snake or ladder" if board[r][c] != -1.  The destination of that snake or ladder is board[r][c].

Note that you only take a snake or ladder at most once per move: if the destination to a snake or ladder is the start of another snake or ladder, you do not continue moving.  (For example, if the board is [[4,-1],[-1,3]], and on the first move your destination square is 2, then you finish your first move at 3, because you do not continue moving to 4.)

Return the least number of moves required to reach square N*N.  If it is not possible, return -1.

Example 1:

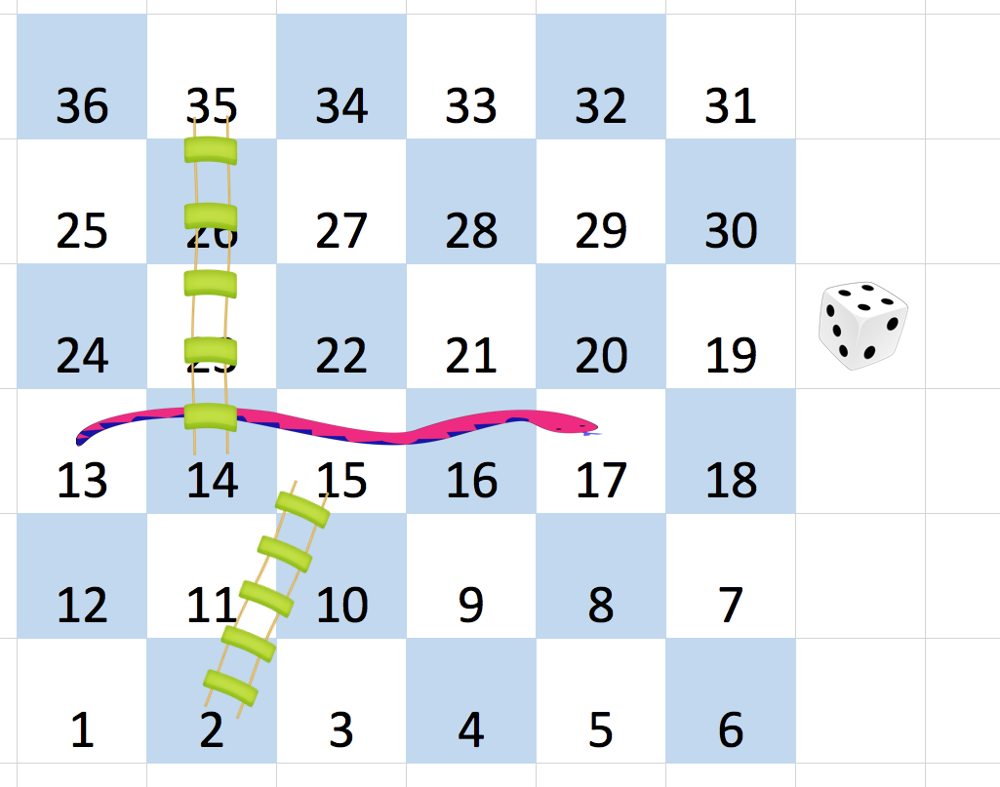
Input: [
[-1,-1,-1,-1,-1,-1],
[-1,-1,-1,-1,-1,-1],
[-1,-1,-1,-1,-1,-1],
[-1,35,-1,-1,13,-1],
[-1,-1,-1,-1,-1,-1],
[-1,15,-1,-1,-1,-1]]
Output: 4
Explanation: 
At the beginning, you start at square 1 [at row 5, column 0].
You decide to move to square 2, and must take the ladder to square 15.
You then decide to move to square 17 (row 3, column 5), and must take the snake to square 13.
You then decide to move to square 14, and must take the ladder to square 35.
You then decide to move to square 36, ending the game.
It can be shown that you need at least 4 moves to reach the N*N-th square, so the answer is 4.

Note:

1. 2 <= board.length = board[0].length <= 20
2. board[i][j] is between 1 and N*N or is equal to -1.
3. The board square with number 1 has no snake or ladder.
4. The board square with number N*N has no snake or ladder.

题意：N x N 的棋盘 board 上，按从 1 到 N*N 的数字给方格编号，编号 从左下角开始，每一行交替方向。 棋盘格中可能存在 “蛇” 或 “梯子”，如果 board[i][j] != -1，则这个蛇或梯子的目的地将会是 board[i][j]。

玩家从棋盘上的方格 1 （总是在最后一行、第一列）开始出发。每一回合，玩家需要从当前方格 x 开始出发，按下述要求前进：

• 选定目标方格：从编号 x+1，x+2，x+3，x+4，x+5，或者 x+6 的方格中选出一个目标方格 s ，目标方格的编号 <= N*N。该选择模拟了掷骰子的情景，无论棋盘大小如何，你的目的地范围只能处于区间 [x+1, x+6] 之间。
• 传送玩家：如果目标方格 S 处存在蛇或梯子，那么玩家会传送到蛇或梯子的目的地。否则，玩家传送到目标方格 S。 

注意，编号为 1  和编号为 N*N 的方格上没有蛇或梯子。玩家在每回合的前进过程中最多只能爬过蛇或梯子一次——就算目的地是另一条蛇或梯子的起点，你也不会继续移动。返回达到方格 N*N 所需的最少移动次数，如果不可能，则返回 -1。

---

解法 BFS

这一题的BFS解法有点麻烦。首先求出编号对应的棋盘坐标，存储在 unordered_map<int, pair<int, int>> rec 中。然后使用一个 bool 数组，记录编号对应的棋盘位置是否被访问，编号入队时即标记访问。接着使用分层BFS，对于当前编号 cur（表示的棋盘坐标）而言下一步只能选择 [cur + 1, cur + 6] 这几个点，分别得到下一步的编号——将下一步编号 next 及其坐标 (x, y) 分成以下几类：

• 没有被访问过的编号：
  • board[x][y] == -1 ：表示不是蛇或者梯子，于是访问并传送到 (x, y) 对应的目标编号 next ；
  • board[x][y] != -1 ：表示是蛇或者梯子：
    • vis[board[x][y]] == false ： 蛇或者梯子的终点是没有被访问过的位置，于是访问并传送到终点编号 board[x][y] ，注意：此时 (x, y) 坐标对应的编号 next 未被访问和标记；
    • 否则表示蛇或者梯子的终点是已经访问过的位置，不进行访问（用于剪枝优化）。
• 已经被访问过的编号：
  • board[x][y] == -1 ：表示不是蛇或梯子，不进行访问（用于剪枝优化）；
  • board[x][y] != -1 ：表示是蛇或梯子，且已被访问，这代表着存在另一次沿着蛇或梯子的、到达此处、且不再继续沿着此处蛇或梯子移动的跳跃，：
    • vis[board[x][y]] == false ：此处蛇或者梯子的终点是没有被访问过的位置，于是访问并传送到终点编号 board[x][y] ，注意：此时 (x, y) 坐标对应的编号 next 已被访问和标记；
    • 否则表示蛇或者梯子的终点是已经访问过的位置，不进行访问（用于剪枝优化）。

如果最后能够到达终点编号 N * N ，返回步数；否则返回 -1 ：

class Solution {
public:
    int snakesAndLadders(vector<vector<int>>& board) {
        int m = board.size(), n = board[0].size(), cnt = 0, i = m - 1, j = -1, mn = m * n;
        unordered_map<int, pair<int, int>> rec;
        while (cnt < mn) { //题目的坐标系真是反人类啊
            while (j + 1 < n) rec[++cnt] = make_pair(i, ++j);
            if (i - 1 >= 0) rec[++cnt] = make_pair(--i, j);
            while (j - 1 >= 0) rec[++cnt] = make_pair(i, --j);
            if (i - 1 >= 0) rec[++cnt] = make_pair(--i, j);
        }
        vector<bool> vis(mn + 1);
        queue<int> q;
        q.push(1);
        vis[1] = true; //入队时访问
        int steps = -1;
        while (!q.empty()) {
            int size = q.size();
            ++steps;
            for (int i = 0; i < size; ++i) {
                int cur = q.front(); q.pop(); 
                if (cur == mn) return steps;
                for (int j = 1; j <= 6; ++j) {
                    int next = cur + j, x = rec[next].first, y = rec[next].second;
                    if (!vis[next]) { //可前往的位置没有被访问过 
                        if (board[x][y] == -1) { //不是蛇或者梯子
                            q.push(next);
                            vis[next] = true; //入队时访问
                        } else if (!vis[board[x][y]]) { //是蛇或者梯子,通往没有被访问的位置
                            q.push(board[x][y]);
                            vis[board[x][y]] = true; //入队时访问
                        }
                    } else if (board[x][y] != -1){ //可前往的位置被访问过,且是蛇或者梯子
                        if (!vis[board[x][y]]) { //蛇或梯子通往没有被访问过的位置
                            q.push(board[x][y]);
                            vis[board[x][y]] = true;
                        }
                    }
                }
            }
        }
        return -1;
    }
};

运行性能如下：

执行用时：32 ms, 在所有 C++ 提交中击败了42.86% 的用户
内存消耗：15.4 MB, 在所有 C++ 提交中击败了28.57% 的用户