文章目录
计算几何作为计算机科学中的一个分支,主要研究解决几何问题的算法,在计算机图形学、科学计算可视化、图形用户界面等领域,都有广泛的应用。这里以二维空间为例,讨论在计算几何中常用的算法设计方法。
10.1 向量运算
在二维空间(即平面上)中,每个输入对象都用一组点
{
p
1
,
p
2
,
…
,
p
n
}
\{ p_1, p_2, \dots, p_n\}
{p1,p2,…,pn} 来表示,其中每个
p
i
=
(
x
i
,
y
i
)
p_i = (x_i, y_i)
pi=(xi,yi) ,
x
i
,
y
i
x_i, y_i
xi,yi 分别是点
p
i
p_i
pi 的行、列坐标,用实数表示。设计点类 Point ,后面分别讨论这些友元函数的设计:
// 计算几何: 点类
class Point {
public:
double x; // 行坐标
double y; // 列坐标
Point() {} // 默认构造函数
Point(double x1, double y1) { // 重载构造函数
x = x1;
y = y1;
}
void disp() { // 输出函数
printf("(%g, %g)", x, y);
}
friend bool operator==(const Point &p1, const Point &p2); // 重载==运算符
friend Point operator+(const Point &p1, const Point &p2); // 重载+运算符
friend Point operator-(const Point &p1, const Point &p2); // 重载-运算符
friend double Dot(const Point &p1, const Point &p2); // 两个向量的点积
friend double Length(Point &p); // 求向量长度
friend int Angle(Point p0, Point p1, Point p2); // 求两线段p0p1和p0p2的夹角
friend double Det(Point p1, Point p2); // 两个向量的叉积
friend double Direction(Point p0, Point p1, Point p2); // 判断两线段p0p1和p0p2的方向
friend double Distance(Point p1, Point p2); // 求两个点的距离
friend double DistPtoSegment(Point p0, Point p1, Point p2); // 求p0到p1p2线段的距离
friend bool InRectAngle(Point p0, Point p1, Point p2); // 判断点p0是否在p1和p2表示的矩阵中
friend bool OnSegment(Point p0, Point p1, Point p2); // 判断点p0是否在p1p2线段上
friend bool Parallel(Point p1, Point p2, Point p3, Point p4); // 判断p1p2和p3p4线段是否平行
friend bool SegIntersect(Point p1, Point p2, Point p3, Point p4); // 判断p1p2和p3p4线段是否相交
friend bool PointInPolygon(Point p0, vector<Point> a); // 判断点p0是否在点集a所形成的多边形内
};
bool operator==(const Point &p1, const Point &p2) { // 重载==运算符
return p1.x == p2.x && p1.y == p2.y;
}
线段是直线在两个定点之间(包含这两个点)的部分,可通过两个点
p
1
,
p
2
p_1, p_2
p1,p2 来表示(向量也是)。通常线段是有向的,有向线段
p
1
p
2
p_1p_2
p1p2 是从起点
p
1
p_1
p1 到终点
p
2
p_2
p2 ,这种既有大小又有方向的量称为向量 vector ,
p
1
p
2
p_1p_2
p1p2 向量的长度或模,为点
p
1
p_1
p1 到
p
2
p_2
p2 的距离,记为
∣
p
1
p
2
∣
|p_1p_2|
∣p1p2∣ 。这里默认将一个点
p
p
p 看成是坐标原点为
(
0
,
0
)
(0, 0)
(0,0) 的向量
p
p
p 。
10.1.1 向量的基本运算
1. 向量加减
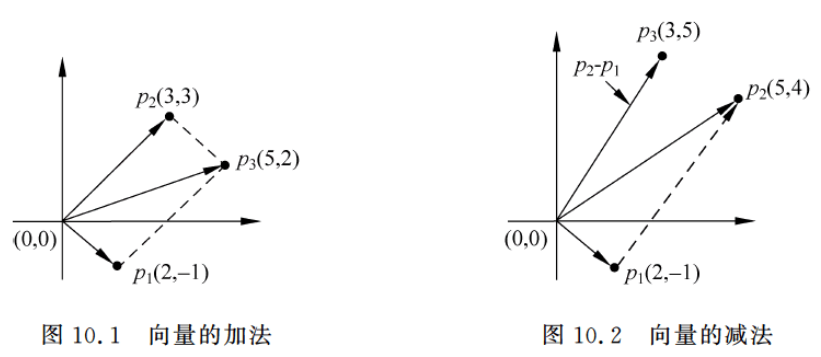
对于两个点表示的两个向量 p 1 , p 2 p_1, p_2 p1,p2(起点均为原点 ( 0 , 0 ) (0, 0) (0,0) ),向量加法定义为 p 1 + p 2 = ( p 1. x + p 2. x , p 1. y + p 2. y ) p_1 + p_2 = (p1.x + p2.x,\ p1.y+p2.y) p1+p2=(p1.x+p2.x, p1.y+p2.y) 其结果仍为一个向量。
向量加法一般可用平行四边形法则,如图10.1所示,两个向量为
p
1
(
2
,
−
1
)
,
p
2
(
3
,
3
)
p_1(2, -1),\ p_2(3, 3)
p1(2,−1), p2(3,3) ,则
p
3
=
p
1
+
p
2
=
(
5
,
2
)
p_3 = p_1 + p_2 = (5, 2)
p3=p1+p2=(5,2) 。
求两个向量
p
1
,
p
2
p_1, p_2
p1,p2 的加法运算的算法如下:
Point operator+(const Point &p1, const Point &p2) { // 重载+运算符
return Point(p1.x + p2.x, p1.y + p2.y);
}
向量减法是向量加法的逆运算,一个向量减去另一个向量等于加上那个向量的负向量,即 p 1 − p 2 = p 1 + ( − p 2 ) = ( p 1 . x − p 2 . x , p 1 . y − p 2 . y ) p_1 - p_2 = p_1 + (-p_2) = (p_1.x - p_2.x, p_1.y - p_2.y) p1−p2=p1+(−p2)=(p1.x−p2.x,p1.y−p2.y)
Point operator-(const Point &p1, const Point &p2) { // 重载-运算符
return Point(p1.x - p2.x, p1.y - p2.y);
}
显然有性质 p 1 + p 2 = p 2 + p 1 , p 1 − p 2 = − ( p 2 − p 1 ) p_1 + p_2 = p_2 + p_1,\ p_1 - p_2 = -(p_2 - p_1) p1+p2=p2+p1, p1−p2=−(p2−p1) 。
如图10.2所示,两个向量为
p
1
(
2
,
−
1
)
,
p
2
(
5
,
4
)
p_1(2, -1),\ p_2(5,4)
p1(2,−1), p2(5,4) ,则
p
3
=
p
2
−
p
1
=
(
3
,
5
)
p_3 = p_2 - p_1 = (3, 5)
p3=p2−p1=(3,5) ,将
p
3
p_3
p3 平移到
p
1
p
2
p_1 p_2
p1p2 处(虚线),可看出
p
3
p_3
p3 的长度与
p
1
,
p
2
p_1, p_2
p1,p2 连接线的长度相同、方向相同。用
∣
p
∣
|p|
∣p∣ 表示向量
p
p
p 的长度,有
∣
p
2
−
p
1
∣
=
|p_2 - p_1| =
∣p2−p1∣= 点
p
1
p_1
p1 与
p
2
p_2
p2 的长度。实际上,
p
2
−
p
1
p_2 - p_1
p2−p1 向量可看成是以
p
1
p_1
p1 为原点的
p
2
p_2
p2 向量。
2. 向量点积运算
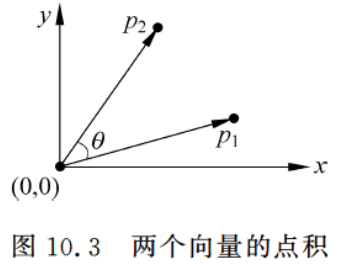
两个向量 p 1 , p 2 p_1, p_2 p1,p2 的点积(或內积),定义为 p 1 ⋅ p 2 = ∣ p 1 ∣ × ∣ p 1 ∣ × cos θ = p 1 . x × p 2 . x + p 1 . y × p 2 . y p_1 \cdot p_2 = |p_1| \times |p_1| \times \cos \theta = p_1.x \times p_2.x + p_1.y \times p_2.y p1⋅p2=∣p1∣×∣p1∣×cosθ=p1.x×p2.x+p1.y×p2.y
其结果是一个标量,其中向量的长度
∣
p
∣
=
p
.
x
2
+
p
.
y
2
|p| = \sqrt{ p.x^2 +p.y^2}
∣p∣=p.x2+p.y2 ,
θ
\theta
θ 表示两个向量的夹角,如图10.3所示。显然有性质
p
1
⋅
p
2
=
p
2
⋅
p
1
p_1 \cdot p_2 = p_2 \cdot p_1
p1⋅p2=p2⋅p1 。
求两个向量
p
1
p_1
p1 和
p
2
p_2
p2 点积的算法如下:
double Dot(const Point &p1, const Point &p2) { // 两个向量的点积
return p1.x * p2.x + p1.y * p2.y;
}
利用点积,求一个向量的长度的算法如下:
double Length(const Point &p) { // 求向量长度
return sqrt(Dot(p, p));
}
可以通过点积的符号,判断两向量相互之间的夹角关系:
- 若 p 1 ⋅ p 2 > 0 p_1 \cdot p_2 > 0 p1⋅p2>0 ,则向量 p 1 p_1 p1 和 p 2 p_2 p2 之间的夹角为锐角;
- 若 p 1 ⋅ p 2 = 0 p_1\cdot p_2 = 0 p1⋅p2=0 ,则向量 p 1 p_1 p1 和 p 2 p_2 p2 之间的夹角为直角;
- 若 p 1 ⋅ p 2 < 0 p_1\cdot p_2 < 0 p1⋅p2<0 ,则向量 p 1 p_1 p1 和 p 2 p_2 p2 之间的夹角为钝角。
对于具有公共起点的两个线段 p 0 p 1 p_0p_1 p0p1 和 p 0 p 2 p_0p_2 p0p2 ,只需要把 p 0 p_0 p0 作为原点就可以,即 p 1 − p 0 p_1 - p_0 p1−p0 和 p 2 − p 0 p_2 - p_0 p2−p0 都是向量,它们的点积为 r = ( p 1 − p 0 ) ⋅ ( p 2 − p 0 ) r = (p_1 - p_0) \cdot (p_2 - p_0) r=(p1−p0)⋅(p2−p0) 。利用上述关系,求两条线段 p 0 p 1 p_0p_1 p0p1 和 p 0 p 2 p_0p_2 p0p2 的夹角的算法如下:
int Angle(Point p0, Point p1, Point p2) { // 求两线段p0p1和p0p2的夹角
double d = Dot(p1 - p0, p2 - p0);
if (d == 0) return 0; // 两线段p1p0和p2p0的夹角为直角
else if (d > 0) return 1; // 两线段p1p0和p2p0的夹角为锐角
else return -1; // 两线段p1p0和p2p0的夹角为钝角
}
3. 向量叉积运算
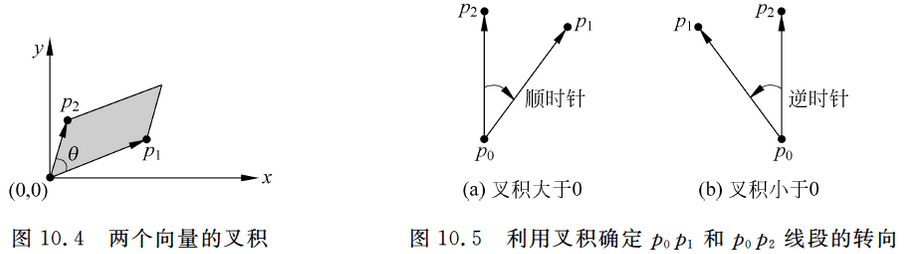
两个向量 p 1 p_1 p1 和 p 2 p_2 p2 的叉积(外积) p 1 × p 2 = ∣ p 1 ∣ × ∣ p 2 ∣ × sin θ = p 1 . x × p 2 . y − p 2 . x × p 1 . y p_1 \times p_2 = |p_1| \times |p_2| \times \sin\theta = p_1.x \times p_2.y - p_2.x \times p_1.y p1×p2=∣p1∣×∣p2∣×sinθ=p1.x×p2.y−p2.x×p1.y ,其结果是一个标量,其中 θ \theta θ 表示两个向量的夹角,如图10.4所示。显然有性质 p 1 × p 2 = − p 2 × p 1 p_1 \times p_2 = -p_2 \times p_1 p1×p2=−p2×p1 。
求两个向量 p 1 , p 2 p_1, p_2 p1,p2 叉积的算法如下:
double Det(const Point &p1, const Point &p2) { // 两个向量的叉积
return p1.x * p2.y - p1.y * p2.x;
}
向量叉积的计算是关于线段算法的核心,如图10.4所示,叉积 p 1 × p 2 p_1 \times p_2 p1×p2 可以看作是由 ( 0 , 0 ) , p 1 , p 2 , p 1 + p 2 (0, 0),\ p_1, \ p_2,\ p_1+p_2 (0,0), p1, p2, p1+p2 所组成的平行四边形的带符号的面积,当 p 1 × p 2 p_1 \times p_2 p1×p2 值为正时,向量 p 1 p_1 p1 可沿着平行四边形内部逆时针旋转到达 p 2 p_2 p2 ;当 p 1 × p 2 p_1 \times p_2 p1×p2 值为负时,向量 p 1 p_1 p1 可沿着平行四边形内部顺时针旋转到达 p 2 p_2 p2 。可通过叉积的符号,判断两个向量相互之间的顺逆时针关系:
- 若 p 1 × p 2 > 0 p_1 \times p_2 > 0 p1×p2>0 ,则 p 1 p_1 p1 在 p 2 p_2 p2 的顺时针方向(图10.4、图10.5 (a)所示);
- 若 p 1 × p 2 < 0 p_1 \times p_2 < 0 p1×p2<0 ,则 p 1 p_1 p1 在 p 2 p_2 p2 的逆时针方向(图10.5 (b)所示);
- 若 p 1 × p 2 = 0 p_1 \times p_2 = 0 p1×p2=0 ,则 p 1 p_1 p1 与 p 2 p_2 p2 共线,但可能同向、也可能反向。
对于具有公共起点的两个线段
p
0
p
1
p_0p_1
p0p1 和
p
0
p
2
p_0p_2
p0p2 ,只需要把
p
0
p_0
p0 作为原点就可以进行向量叉积运算,即
p
1
−
p
0
p_1 - p_0
p1−p0 和
p
2
−
p
0
p_2 - p_0
p2−p0 都是向量,它们的叉积为
r
=
(
p
1
−
p
0
)
×
(
p
2
−
p
0
)
=
(
p
1
.
x
−
p
0
.
x
)
×
(
p
2
.
y
−
p
0
.
y
)
−
(
p
2
.
x
−
p
0
.
x
)
×
(
p
1
.
y
−
p
0
.
y
)
r = (p_1 - p_0) \times (p_2 - p_0) = (p_1.x - p_0.x) \times (p_2.y - p_0.y) - (p_2.x - p_0.x) \times (p_1.y - p_0.y)
r=(p1−p0)×(p2−p0)=(p1.x−p0.x)×(p2.y−p0.y)−(p2.x−p0.x)×(p1.y−p0.y) ,可通过该叉积的符号与上述说明,判断两线段相互之间的顺逆时针关系(超过
180
°
180\degree
180° 就会产生不同的顺逆时针关系)。
判断两条线段
p
0
p
1
p_0p_1
p0p1 和
p
0
p
2
p_0p_2
p0p2 方向的算法如下:
double Direction(Point p0, Point p1, Point p2) { // 判断两线段p0p1和p0p2的方向
double d = Det(p1 - p0, p2 - p0);
if (d == 0) return 0; // p0,p1,p2三点共线
else if (d > 0) return 1; // p0p1在p0p2的顺时针方向上
else return -1; // p0p1在p0p2的逆时针方向上
}
4. 两个点的距离
两个点
p
1
,
p
2
p_1, p_2
p1,p2 之间的距离为
(
p
1
.
x
−
p
2
.
x
)
2
+
(
p
1
.
y
−
p
2
.
y
)
2
\sqrt{(p_1.x - p_2.x)^2 + (p_1.y - p_2.y)^2}
(p1.x−p2.x)2+(p1.y−p2.y)2 。可将
p
1
,
p
2
p_1,p_2
p1,p2 视为一个向量,(用 Length 函数即內积)求其长度;或直接写出数学公式:
double Distance(Point p1, Point p2) { // 求两个点的距离
return sqrt((p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y));
}
5. 点到线段的距离
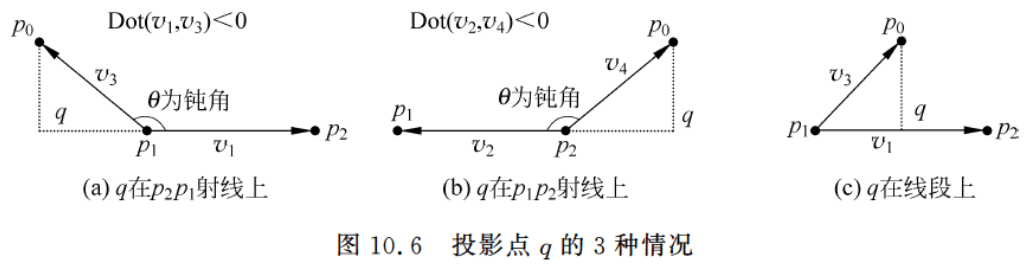
求点 p 0 p_0 p0 到线段 p 1 p 2 p_1p_2 p1p2 的距离。设 p 0 p_0 p0 在线段 p 1 p 2 p_1p_2 p1p2 上的投影点为 q q q ,设向量 v 1 = p 2 − p 1 , v 2 = p 1 − p 2 , v 3 = p 0 − p 1 , v 4 = p 0 − p 2 v_1 = p_2 - p_1,\ v_2 = p_1 - p_2,\ v_3 = p_0 - p_1,\ v_4 = p_0 - p_2 v1=p2−p1, v2=p1−p2, v3=p0−p1, v4=p0−p2 。点 q q q 的三种可能情况如图10.6所示。
- 若满足图10.6 a)所示的情况, p 0 p_0 p0 到线段 p 1 p 2 p_1p_2 p1p2 的距离为向量 v 3 v_3 v3 的长度;
- 若满足图10.6 b)所示的情况, p 0 p_0 p0 到线段 p 1 p 2 p_1p_2 p1p2 的距离为向量 v 4 v_4 v4 的长度;
- 若满足图10.6 c)所示的情况,
p
0
p_0
p0 到线段
p
1
p
2
p_1p_2
p1p2 的距离为向量
v
1
v_1
v1 和
v
3
v_3
v3 叉积的绝对值(平行四边形的面积)除以底长。可设
v
1
,
v
3
v_1, v_3
v1,v3 的夹角为
θ
\theta
θ ,则
sin
θ
=
∣
p
0
q
∣
∣
p
0
p
1
∣
\sin \theta = \dfrac{ | p_0q|} { | p_0 p_1| }
sinθ=∣p0p1∣∣p0q∣ ,则
∣
p
0
q
∣
=
sin
θ
⋅
∣
p
0
p
1
∣
| p_0 q| =\sin \theta \cdot |p_0p_1|
∣p0q∣=sinθ⋅∣p0p1∣ ,即
v
1
×
v
3
v_1 \times v_3
v1×v3 的绝对值除以
∣
p
1
p
2
∣
|p_1p_2|
∣p1p2∣ 。
对应的算法如下:
double DistPtoSegment(Point p0, Point p1, Point p2) { // 求p0到p1p2线段的距离
Point v1 = p2 - p1, v2 = p1 - p2, v3 = p0 - p1, v4 = p0 - p2;
if (p1 == p2) return Length(p0 - p1); // 两点重合
if (Dot(v1, v3) < 0)
return Length(v3);
else if (Dot(v2, v4) < 0)
return Length(v4);
else
return fabs(Det(v1, v3)) / Length(v1);
}
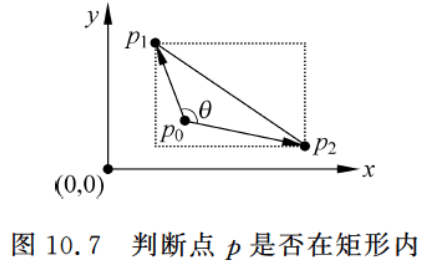
10.1.2 判断一个点是否在一个矩形内
设一个矩形的左上角为点 p 1 p_1 p1 、右下角为点 p 2 p_2 p2 ,另有一个点 p 0 p_0 p0 ,现要判断该点是否在指定的矩形内。
将
p
0
p
1
p_0p_1
p0p1 和
p
0
p
2
p_0p_2
p0p2 看成是具有公共起点的两个线段,把
p
0
p_0
p0 作为原点,显然
p
0
p
1
p_0p_1
p0p1 和
p
0
p
2
p_0p_2
p0p2 两线段的夹角
θ
\theta
θ 为直角或钝角时,点
p
0
p_0
p0 就落在该矩形内(含点
p
1
,
p
2
p_1, p_2
p1,p2 ),如图10.7所示。所以,点
p
0
p_0
p0 在该矩形内应满足条件
(
p
1
−
p
0
)
⋅
(
p
2
−
p
0
)
≤
0
(p_1 - p_0) \cdot (p_2 - p_0) \le 0
(p1−p0)⋅(p2−p0)≤0 。
对应的判断算法如下:
bool InRectAngle(Point p0, Point p1, Point p2) { // 判断点p0是否在p1和p2表示的矩阵中
return Dot(p1 - p0, p2 - p0) <= 0;
}
另一种更直观的判断方法是, p 0 p_0 p0 在该矩形内应满足以下条件:
min(p1.x, p2.x) <= p0.x <= max(p1.x, p2.x) &&
min(p1.y, p2.y) <= p0.y <= max(p1.y, p2.y)
10.1.3 判断一个点是否在一条线段上
设点为 p 0 p_0 p0 、线段为 p 1 p 2 p_1p_2 p1p2 ,若点 p 0 p_0 p0 在该线段上(含点 p 1 , p 2 p_1, p_2 p1,p2 ),应同时满足两个条件:一是点 p 0 p_0 p0 在线段 p 1 p 2 p_1p_2 p1p2 所在的直线上;二是点 p 0 p_0 p0 在以 p 1 , p 2 p_1, p_2 p1,p2 为对角顶点的矩形内。前者保证点 p 0 p_0 p0 在直线 p 1 p 2 p_1p_2 p1p2 上,后者保证点 p 0 p_0 p0 不在线段 p 1 p 2 p_1p_2 p1p2 的延长线或反向延长线上。
- 点 p 0 p_0 p0 在线段 p 1 p 2 p_1p_2 p1p2 所在的直线上,应满足的条件是 ( p 1 − p 0 ) × ( p 2 − p 0 ) = 0 (p_1 - p_0) \times (p_2 - p_0) = 0 (p1−p0)×(p2−p0)=0 ;
- 点 p 0 p_0 p0 在以 p 1 , p 2 p_1, p_2 p1,p2 为对角顶点的矩形内,应满足的条件是 ( p 1 − p 0 ) ⋅ ( p 2 − p 0 ) ≤ 0 (p_1 - p_0) \cdot (p_2 - p_0) \le 0 (p1−p0)⋅(p2−p0)≤0 。
bool OnSegment(Point p0, Point p1, Point p2) { // 判断点p0是否在p1p2线段上
return Det(p1 - p0, p2 - p0) == 0 && Dot(p1 - p0, p2 - p0) <= 0;
}
10.1.4 判断两条线段是否平行
设两条线段为 p 1 p 2 p_1p_2 p1p2 和 p 3 p 4 p_3p_4 p3p4 ,如果它们的夹角为零,则是平行的,所以两条线段 p 1 p 2 p_1p_2 p1p2 和 p 3 p 4 p_3p_4 p3p4 平行应满足的条件是 ( p 2 − p 1 ) × ( p 4 − p 3 ) = 0 (p_2 - p_1) \times (p_4 - p_3) = 0 (p2−p1)×(p4−p3)=0 。
bool Parallel(Point p1, Point p2, Point p3, Point p4) { // 判断p1p2和p3p4线段是否平行
return Det(p2 - p1, p4 - p3) == 0;
}
10.1.5 判断两条线段是否相交
对于两条直线,可以不平行、即相交,但对线段则不然。设两条线段为 p 1 p 2 p_1p_2 p1p2 和 p 3 p 4 p_3p_4 p3p4 ,如图10.8所示,要判断它们是否相交(包括端点),只要点 p 1 , p 2 p_1, p_2 p1,p2 在线段 p 3 p 4 p_3p_4 p3p4 的两边且点 p 3 , p 4 p_3, p_4 p3,p4 在线段 p 1 p 2 p_1p_2 p1p2 的两边,那么这两条线段必然相交。
那么如何判断两点是否在一条线段的两边呢?令:
-
d
1
=
p
3
p
1
×
p
3
p
4
d_1 = p_3 p_1 \times p_3 p_4
d1=p3p1×p3p4 等于
Direction(p3, p1, p4),求 p 3 p 1 p_3p_1 p3p1 在 p 3 p 4 p_3p_4 p3p4 的哪个方向上; -
d
2
=
p
3
p
2
×
p
3
p
4
d_2 = p_3 p_2 \times p_3 p_4
d2=p3p2×p3p4 等于
Direction(p3, p2, p4),求 p 3 p 2 p_3p_2 p3p2 在 p 3 p 4 p_3p_4 p3p4 的哪个方向上; -
d
3
=
p
1
p
3
×
p
1
p
2
d_3 = p_1 p_3 \times p_1 p_2
d3=p1p3×p1p2 等于
Direction(p1, p3, p2),求 p 1 p 3 p_1p_3 p1p3 在 p 1 p 2 p_1p_2 p1p2 的哪个方向上; -
d
4
=
p
1
p
4
×
p
1
p
2
d_4 = p_1 p_4 \times p_1 p_2
d4=p1p4×p1p2 等于
Direction(p1, p4, p2),求 p 1 p 4 p_1p_4 p1p4 在 p 1 p 2 p_1p_2 p1p2 的哪个方向上。
这两条线段相交的情况如下:
- d 1 < 0 d_1 < 0 d1<0( p 3 p 1 p_3p_1 p3p1 在 p 3 p 4 p_3p_4 p3p4 的逆时针方向上)且 d 2 > 0 d_2 > 0 d2>0( p 3 p 2 p_3p_2 p3p2 在 p 3 p 4 p_3p_4 p3p4 的顺时针方向上),图10.8就是这种情况;
-
d
1
>
0
d_1 > 0
d1>0(
p
3
p
1
p_3p_1
p3p1 在
p
3
p
4
p_3p_4
p3p4 的顺时针方向上)且
d
2
<
0
d_2 < 0
d2<0(
p
3
p
2
p_3p_2
p3p2 在
p
3
p
4
p_3p_4
p3p4 的逆时针方向上),图10.8中的
p
1
,
p
2
p_1, p_2
p1,p2 交换就是这种情况。
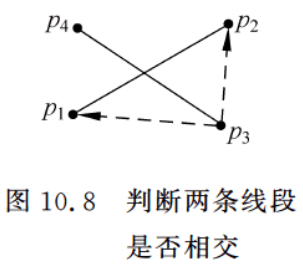
上述两种情况表示 p 1 , p 2 p_1, p_2 p1,p2 两个点在线段 p 3 p 4 p_3p_4 p3p4 的两边,即条件为 d 1 × d 2 < 0 d_1 \times d_2 < 0 d1×d2<0 。同理,若有 d 3 × d 4 < 0 d_3 \times d_4 < 0 d3×d4<0 ,则 p 3 , p 4 p_3, p_4 p3,p4 两个点在线段 p 1 p 2 p_1p_2 p1p2 的两边。
另外,若 d i = 0 ( 1 ≤ i ≤ 4 ) d_i = 0\ (1 \le i \le 4) di=0 (1≤i≤4) ,还需要判断对应的点是否在线段上。例如,若 d 1 = 0 d_1 = 0 d1=0 ,表示 p 1 , p 3 , p 4 p_1, p_3, p_4 p1,p3,p4 三点共线,还需要判断点 p 1 p_1 p1 在 p 3 p 4 p_3p_4 p3p4 线段上。对应的判断算法如下:
bool SegIntersect(Point p1, Point p2, Point p3, Point p4) { // 判断p1p2和p3p4线段是否相交
int d1, d2, d3, d4;
d1 = Direction(p3, p1, p4); // 求p3p1在p3p4的哪个方向上
d2 = Direction(p3, p2, p4); // 求p3p2在p3p4的哪个方向上
d3 = Direction(p1, p3, p2); // 求p1p3在p1p2的哪个方向上
d4 = Direction(p1, p4, p2); // 求p1p4在p1p2的哪个方向上
if (d1 * d2 < 0 && d3 * d4 < 0) return true;
if (d1 == 0 && OnSegment(p1, p3, p4)) // 若d1为0且p1在p3p4线段上
return true;
else if (d2 == 0 && OnSegment(p2, p3, p4)) // 若d2为0且p2在p3p4线段上
return true;
else if (d3 == 0 && OnSegment(p3, p1, p2)) // 若d3为0且p3在p1p2线段上
return true;
else if (d4 == 0 && OnSegment(p4, p1, p2)) // 若d4为0且p4在p1p2线段上
return true;
else
return false;
}
10.1.6 判断一个点是否在多边形内
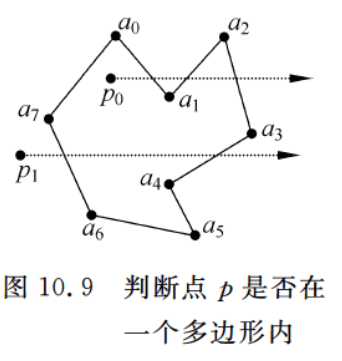
一个多边形由 n n n 个顶点 a [ 0... n ] a[0...n] a[0...n] 构成( a [ n ] = a [ 0 ] a[n] = a[0] a[n]=a[0]),假设其所有的边不相交,称之为简单多边形,这里讨论的多边形默认都是简单多边形。现有一个点 p 0 p_0 p0 ,要判断点 p 0 p_0 p0 是否在该多边形内(含边界)。
其基本思想是从点
p
0
p_0
p0 引一条水平向右的射线,统计该射线与多边形相交的情况,如果相交次数是奇数,那么就在多边形内;否则在多边形外。例如,如图10.9所示,多边形由
8
8
8 个顶点构成,从点
p
0
p_0
p0 引出的射线与多边形相交的交点个数为
3
3
3 ,它在多边形内;而从点
p
1
p_1
p1 引出的射线与多边形相交的交点个数为
2
2
2 ,它在多边形外。
对于多边形的一条边
p
1
p
2
p_1p_2
p1p2 ,它构成的直线的方程为
y
−
p
1
.
y
=
k
(
x
−
p
1
.
x
)
y - p_1.y = k(x - p_1.x)
y−p1.y=k(x−p1.x) ,其斜率
k
=
p
2
.
y
−
p
1
.
y
p
2
.
x
−
p
1
.
x
k = \dfrac{p_2.y - p_1.y} {p_2.x - p_1.x}
k=p2.x−p1.xp2.y−p1.y ,所以有
x
=
y
−
p
1
.
y
k
+
p
1
.
x
=
(
y
−
p
1
.
y
)
(
p
2
.
x
−
p
1
.
x
)
p
2
.
y
−
p
1
.
y
+
p
1
.
x
x = \dfrac{y - p_1.y} {k} + p_1.x = \dfrac{ (y - p_1.y)(p_2.x - p_1.x) } { p_2.y - p_1.y } +p_1.x
x=ky−p1.y+p1.x=p2.y−p1.y(y−p1.y)(p2.x−p1.x)+p1.x 从点
p
0
p_0
p0 引一条水平向右的射线的方程为
y
=
p
0
y
y = p_0 y
y=p0y 。如果这两条直线有交点,则交点为
(
x
,
p
0
.
y
)
(x, p_0.y)
(x,p0.y) ,其中
x
=
(
p
0
.
y
−
p
1
.
y
)
(
p
2
.
x
−
p
1
.
x
)
p
2
.
y
−
p
1
.
y
+
p
1
.
x
x = \dfrac{ (p_0.y - p_1.y )(p_2.x - p_1.x) } { p_2.y - p_1.y } +p_1.x
x=p2.y−p1.y(p0.y−p1.y)(p2.x−p1.x)+p1.x
注意,上述公式中这样变形,使得 p 1 p 2 p_1p_2 p1p2 为垂直线时 1 k = 0 \dfrac{1}{k} = 0 k1=0 、为水平线时 1 k = ∞ \dfrac{1}{k } = \infin k1=∞ ,加上射线为水平线,这都要求特判 p 1 p 2 p_1p_2 p1p2 为水平线的情况。
判断点 p 0 p_0 p0 是否在多边形 a [ 0... n ] a[0...n] a[0...n] 中的步骤如下:
- 置 c n t = 0 cnt = 0 cnt=0 , i i i 从 0 0 0 到 n n n 循环;
-
p
1
=
a
[
i
]
,
p
2
=
a
[
i
+
1
]
p_1 = a[i],\ p_2 = a[i + 1]
p1=a[i], p2=a[i+1] ,若
p
0
p_0
p0 在
p
1
p
2
p_1p_2
p1p2 线段上,则返回
true; - 若 p 1 p 2 p_1p_2 p1p2 是一条水平线,或者 p 0 p_0 p0 在 p 1 p 2 p_1p_2 p1p2 线段的上方或下方,则没有交点,转向下一条线段进行求解。
- 求出射线与线段 p 1 p 2 p_1p_2 p1p2 的交点的 x x x ;
- 若
x
>
p
0
.
x
x > p_0.x
x>p0.x ,则交点个数
cnt加一; - 循环结束后,返回
cnt % 2 == 1值,即交点个数为奇数表示该点在多边形内。
对应的判断算法如下:
bool PointInPolygon(Point p0, vector<Point> a) { // 判断点p0是否在点集a所形成的多边形内
int i, cnt = 0;
double x;
Point p1, p2;
for (int i = 0; i < a.size(); ++i) {
p1 = a[i]; p2 = a[i + 1]; // 取多边形的一条边
if (OnSegment(p0, p1, p2)) // 如果点p0在多边形边p1p2线段上,返回true
return true;
// 以下求解y=p0.y与p1p2的交点
if (p1.y == p2.y) continue; // 如果p1p2是水平线,直接跳过
// 以下两种情况是交点在p1p2的延长线上、而非p1p2线段上
if (p0.y < p1.y && p0.y < p2.y) continue; // p0在p1p2线段下方,直接跳过
if (p0.y >= p1.y && p0.y >= p2.y) continue; // p0在p1p2线段上方,直接跳过
x = (p0.y - p1.y) * (p2.x - p1.x) / (p2.y - p1.y) + p1.x; // 求交点坐标的x值
if (x > p0.x) ++cnt; // 只统计射线的一边
}
return (cnt % 2 == 1);
}
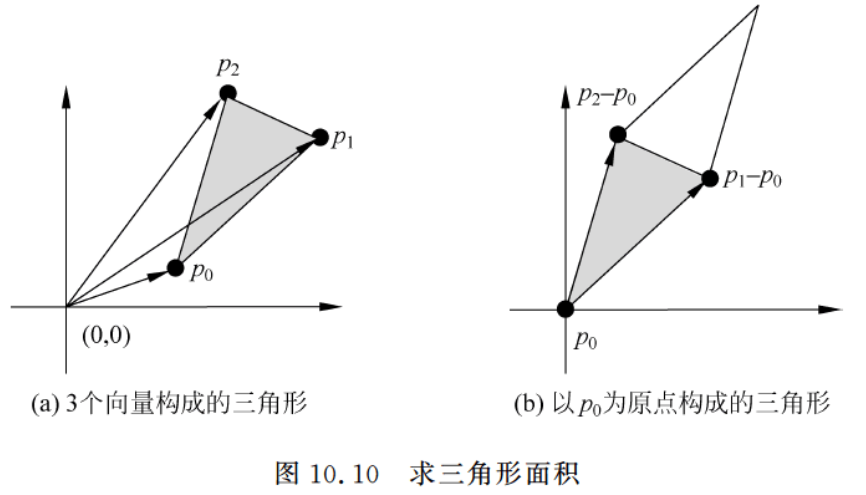
10.1.7 求三个点构成的三角形的面积
对于三个顶点 p 0 , p 1 , p 2 p_0, p_1, p_2 p0,p1,p2 构成的三角形,求面积有多种计算公式。从向量的角度看, 3 3 3 个向量构成的三角形如图10.10 a)所示,可将其两条边看成以 p 0 p_0 p0 为原点的三角形,这两条边分别是 p 1 − p 0 p_1 - p_0 p1−p0 和 p 2 − p 0 p_2 - p_0 p2−p0 ,如图10.10 b)所示,则该三角形面积 S ( p 0 , p 1 , p 2 ) S(p_0, p_1, p_2) S(p0,p1,p2) 等于以 p 1 − p 0 p_1 - p_0 p1−p0 和 p 2 − p 0 p_2 - p_0 p2−p0 向量构成的平行四边形面积的一半,即 S ( p 0 , p 1 , p 2 ) = ( p 1 − p 0 ) × ( p 2 − p 0 ) 2 S(p_0, p_1, p_2) =\dfrac{ (p_1 - p_0) \times (p_2 - p_0) } {2} S(p0,p1,p2)=2(p1−p0)×(p2−p0)
而
(
p
1
−
p
0
)
×
(
p
2
−
p
0
)
(p_1 - p_0) \times (p_2 - p_0)
(p1−p0)×(p2−p0) 的结果有正有负,所以
S
(
p
0
,
p
1
,
p
2
)
=
(
p
1
−
p
0
)
×
(
p
2
−
p
0
)
/
2
S(p_0, p_1, p_2) = (p_1 - p_0) \times (p_2 - p_0) / 2
S(p0,p1,p2)=(p1−p0)×(p2−p0)/2 称为有向面积,实际面积为其绝对值。对应的算法如下:
double triangleArea(Point p0, Point p1, Point p2) { // 求三边形面积
return fabs(Det(p1 - p0, p2 - p0)) / 2;
}
根据向量叉积运算规则有:
- 若 ( p 1 − p 0 ) (p_1 - p_0) (p1−p0) 在 ( p 2 − p 0 ) (p_2 - p_0) (p2−p0) 的顺时针方向,则 ( p 1 − p 0 ) × ( p 2 − p 0 ) > 0 (p_1 - p_0)\times (p_2 - p_0) > 0 (p1−p0)×(p2−p0)>0 。图10.10中就是这种情况。
- 若 ( p 1 − p 0 ) (p_1 - p_0) (p1−p0) 在 ( p 2 − p 0 ) (p_2 - p_0) (p2−p0) 的逆时针方向,则 ( p 1 − p 0 ) × ( p 2 − p 0 ) < 0 (p_1 - p_0)\times (p_2 - p_0) < 0 (p1−p0)×(p2−p0)<0 。
10.1.8 求一个多边形的面积
若一个多边形由
n
n
n 个顶点构成,采用 vector<Point> p 存储,求其面积的方法有多种。常用的是采用三角形剖分的方法,取一个顶点作为剖分出的三角形的顶点,三角形的其他两个顶点为多边形上相邻的点对,如图10.11所示。
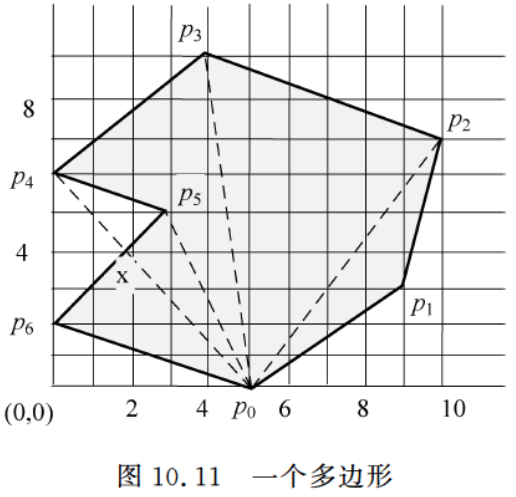
已知三角形的
3
3
3 个顶点向量,可通过向量叉积得到其面积,还可以通过向量叉积解决凹多边形中重复面积的计算问题。在图10.11中
7
7
7 个顶点分别是
p
0
(
5
,
0
)
,
p
1
(
9
,
3
)
,
p
2
(
10
,
7
)
,
p
3
(
4
,
9
)
,
p
4
(
0
,
6
)
,
p
5
(
3
,
5
)
,
p
6
(
0
,
2
)
p_0(5, 0),\ p_1(9, 3),\ p_2(10, 7),\ p_3(4, 9),\ p_4(0, 6),\ p_5(3, 5),\ p_6(0, 2)
p0(5,0), p1(9,3), p2(10,7), p3(4,9), p4(0,6), p5(3,5), p6(0,2) ,以
p
0
p_0
p0 为剖分点,求解过程如下:
- ( p 1 − p 0 ) × ( p 2 − p 0 ) / 2 = 6.5 (p_1 - p_0) \times (p_2 - p_0)/ 2 = 6.5 (p1−p0)×(p2−p0)/2=6.5 ,得到 S ( p 0 , p 1 , p 2 ) = 6.5 S(p_0, p_1, p_2) = 6.5 S(p0,p1,p2)=6.5 , p 0 p 1 p_0p_1 p0p1 在 p 0 p 2 p_0p_2 p0p2 的顺时针方向;
- ( p 2 − p 0 ) × ( p 3 − p 0 ) / 2 = 26 (p_2 - p_0) \times (p_3 - p_0) / 2 = 26 (p2−p0)×(p3−p0)/2=26 ,得到 S ( p 0 , p 2 , p 3 ) = 26 S(p_0, p_2, p_3) = 26 S(p0,p2,p3)=26 ;
- ( p 3 − p 0 ) × ( p 4 − p 0 ) / 2 = 19.5 (p_3 - p_0) \times (p_4 - p_0) / 2 = 19.5 (p3−p0)×(p4−p0)/2=19.5 ,得到 S ( p 0 , p 3 , p 4 ) = 19.5 S(p_0, p_3, p_4) = 19.5 S(p0,p3,p4)=19.5 ,含 p 4 − p 5 − x p_4 - p_5 - x p4−p5−x 部分(不应该包括在多边形面积中)面积和 p 0 − p 5 − x p_0 - p_5 - x p0−p5−x 部分面积;
- ( p 4 − p 0 ) × ( p 5 − p 0 ) / 2 = − 6.5 (p_4 - p_0) \times (p_5 - p_0) / 2 = -6.5 (p4−p0)×(p5−p0)/2=−6.5( p 0 p 4 p_0p_4 p0p4 在 p 0 p 5 p_0p_5 p0p5 的逆时针方向),得到 S ( p 0 , p 4 , p 5 ) = − 6.5 S(p_0, p_4, p_5) = -6.5 S(p0,p4,p5)=−6.5 ,其绝对值含 p 4 − p 5 − x p_4 - p_5 - x p4−p5−x 部分面积和 p 0 − p 5 − x p_0 - p_5 - x p0−p5−x 部分面积。由于为负数, S ( p 0 , p 3 , p 4 ) + S ( p 0 , p 4 , p 5 ) S(p_0, p_3, p_4) + S(p_0, p_4, p_5) S(p0,p3,p4)+S(p0,p4,p5) 恰好得到 p 0 − p 3 − p 4 − p 5 p_0 - p_3 - p_4 - p_5 p0−p3−p4−p5 部分的面积;
- ( p 5 − p 0 ) × ( p 6 − p 0 ) / 2 = 10.5 (p_5 - p_0) \times (p_6 - p_0) / 2 = 10.5 (p5−p0)×(p6−p0)/2=10.5 ,得到 S ( p 0 , p 5 , p 6 ) = 10.5 S(p_0, p_5, p_6) = 10.5 S(p0,p5,p6)=10.5 ;
- 上述所有的有向面积相加,得到多边形的面积 56 56 56 。
对应的算法如下:
double polyArea(vector<Point> p) { // 求多边形的面积
double ans = 0.0;
for (int i = 1; i < p.size() - 1; ++i)
ans += Det(p[i] - p[0], p[i + 1] - p[0]);
return fabs(ans) / 2; // 累计有向面积结果的绝对值
}
10.2 求解凸包问题
【数据结构和算法设计】算法篇(10) 计算几何(3) 凸包问题
10.3 求解最近点对问题
【数据结构和算法设计】算法篇(10) 计算几何(3) 最近点对问题
10.4 求解最远点对问题
【数据结构和算法设计】算法篇(10) 计算几何(4) 最远点对问题
10.5 其他题目


























 335
335











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










